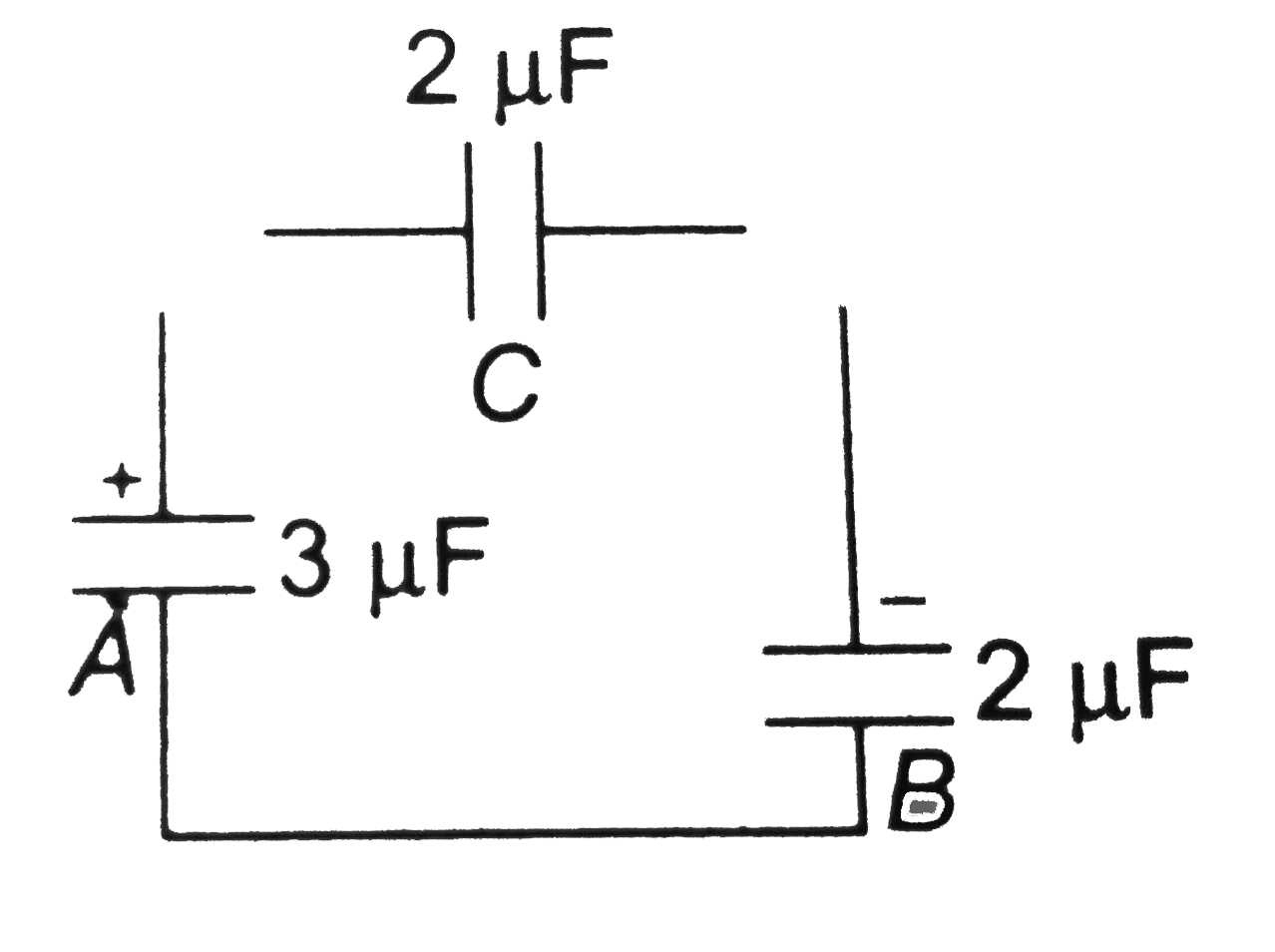
Two capacitors A and B with capacities $3 μ F$ and $2 μ F$ are charged to a potential differece of $100 V$ and $180 V$ , respectively. The plates ot the capacitors are connected as shown in, with one wire free from each capacitor. The upper plate of A is positive and that of B is negative An uncharged $2 μ F$ capacitor C with lead wires falls on the free ends to complete the circuit.
i. Calculate the final charge on the three capacitors,
ii. Find the amount of electrostatic energy stored in the system before and after the completion of the circuit.
.

Video Solution

Text Solution

Verified by Experts

(i) Method 1 : Initial charge on capacitor $A$ is $q_{A} = 3 \times 100 = 300 μ C$ . Initial charge on capacitor $B$ is $q_{B} = 2 \times 180 = 360 μ C$ . After completing the circuit, let the charge on capacitor $A$ be $q_{1}$ , on $B$ be $q_{2}$ , and on $C$ be $q_{3}$ with polarities as shown in. Applying conservation of charge for plates $2$ and $3$ , we get
$q_{1} + q_{3} = - 360 + 0 = 300$ (i)
Applying conservation of charge for plates $4$ and $5$ , we get
$- q_{2} - q_{3} = - 360 + 0$ or $q_{2} + q_{3} = 360$ (ii)
Applying Kirchhoff's law in the whole cirucuit, we get
$\frac{q_{1}}{3} - \frac{q_{3}}{2} + \frac{q_{2}}{2} = 0$ (iii)
On solving, we get $q_{1} = 90 μ C, q_{2} = 150 μ C$ , and $q_{3} = 210 μ C$

Method 2 : After completing the circuit, let the charge $q$ flow in the circuit in the clockwise direction. Then the final charges on the capacitors will be as shown in.

Applying Kirchhoff's law, we get
$\frac{300 - q}{3} - \frac{q}{2} + \frac{360 - q}{2} = 0$ or $q = 210 μ C$
Now charge on all three capacitors can be found.
(ii) Initially, energy stored is
$U_{i} = \frac{1}{2} \times 3 \times 10^{- 6} \times {(100)}^{2} + \frac{1}{2} \times 2 \times 10^{- 6} {(180)}^{2}$
$= 4.74 \times 10^{- 2} J$
Finally, the energy stored is
$U_{f} = \frac{{(90 \times 10^{- 6})}^{2}}{2 \times 3 \times 10^{- 6}} + \frac{{(150 \times 10^{- 6})}^{2}}{2 \times 2 \times 10^{- 6}} + \frac{{(210 \times 6^{- 6})}^{2}}{2 \times 2 \times 10^{- 6}}$
$= 1.8 \times 10^{- 2} J$

Updated on:21/07/2023

Two capacitors A and B with capacities $C_{1} and C_{2}$ are charged to potential difference of $V_{1} and V_{2}$ respectively. The plates of the capacitors are connected as shown in the figure with one wire free from each capacitor. The upper plate of A is positive and that of B is negative. An uncharged capacitor of capacitance $C_{3}$ and lead wires falls on the free ends to complete circuit, then

Athe final charge on each capacitor are same to each other
Bthe final sum of charge on plates a and d is $C_{1} V_{1}$ .
Cthe final sum of charge on plates b and g is $C_{2} V_{2} - C_{1} V_{1}$
Dboth (b) and(c ) are correct.
Two capacitors of $2 μ F$ and $3 μ F$ are charged to $150 V$ and $120 V$ , respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity $1.5 μ F$ falls to the free end of the wire. Then

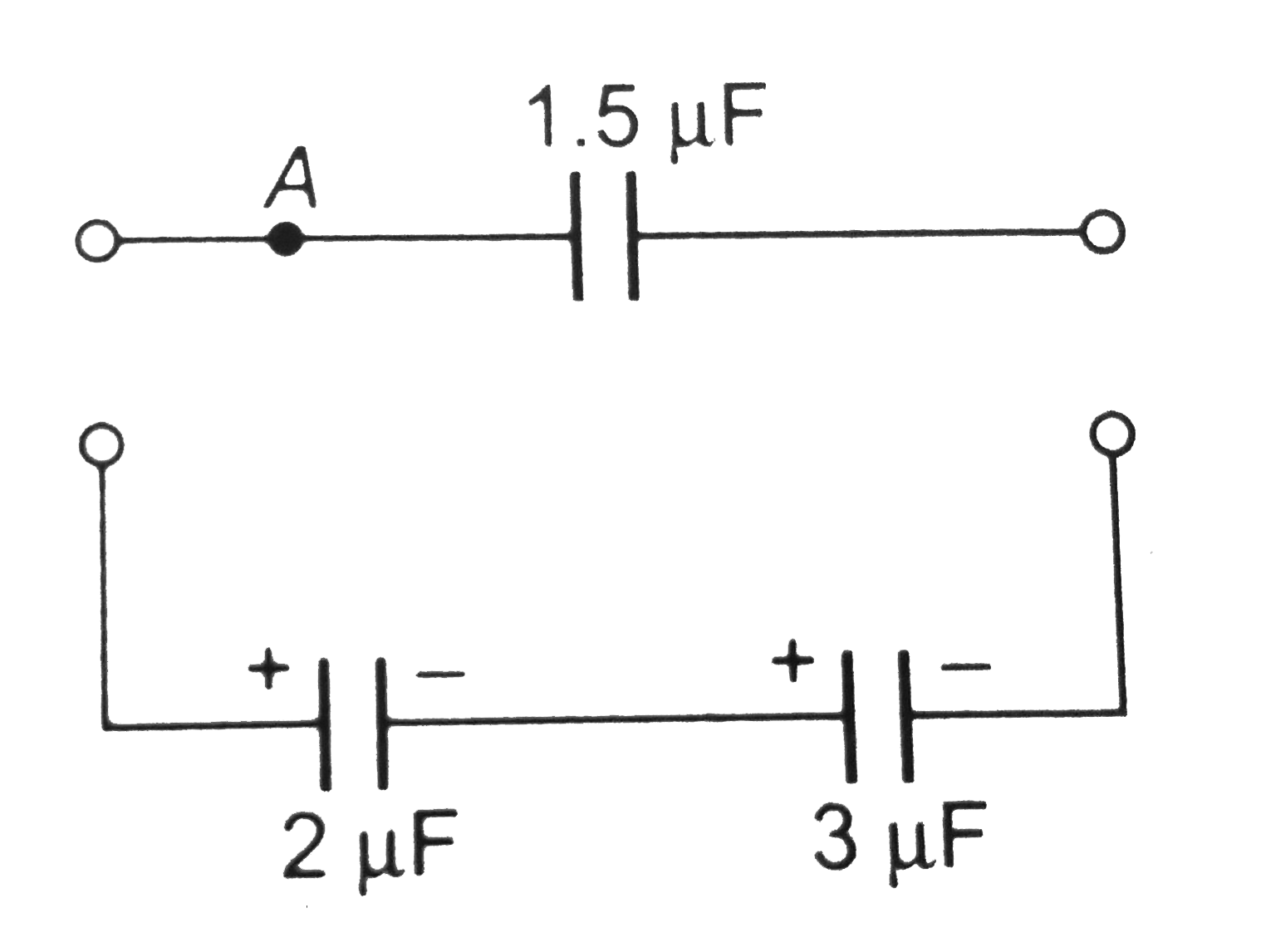Achargeg on $1.5 μ F$ capacitor is $180 μ F$
Bcharge on $2 μ F$ capacitor is $120 μ F$
Cpositive chasrge flows through A from right to left
Dpositive charge flows through A from left to right
Two capacitors of capacitances $10 μ F and 20 μ F$ are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
A66.67 V, 33.33 V
B60 V, 40 V
C50 V, 50 V
D90 V, 10 V