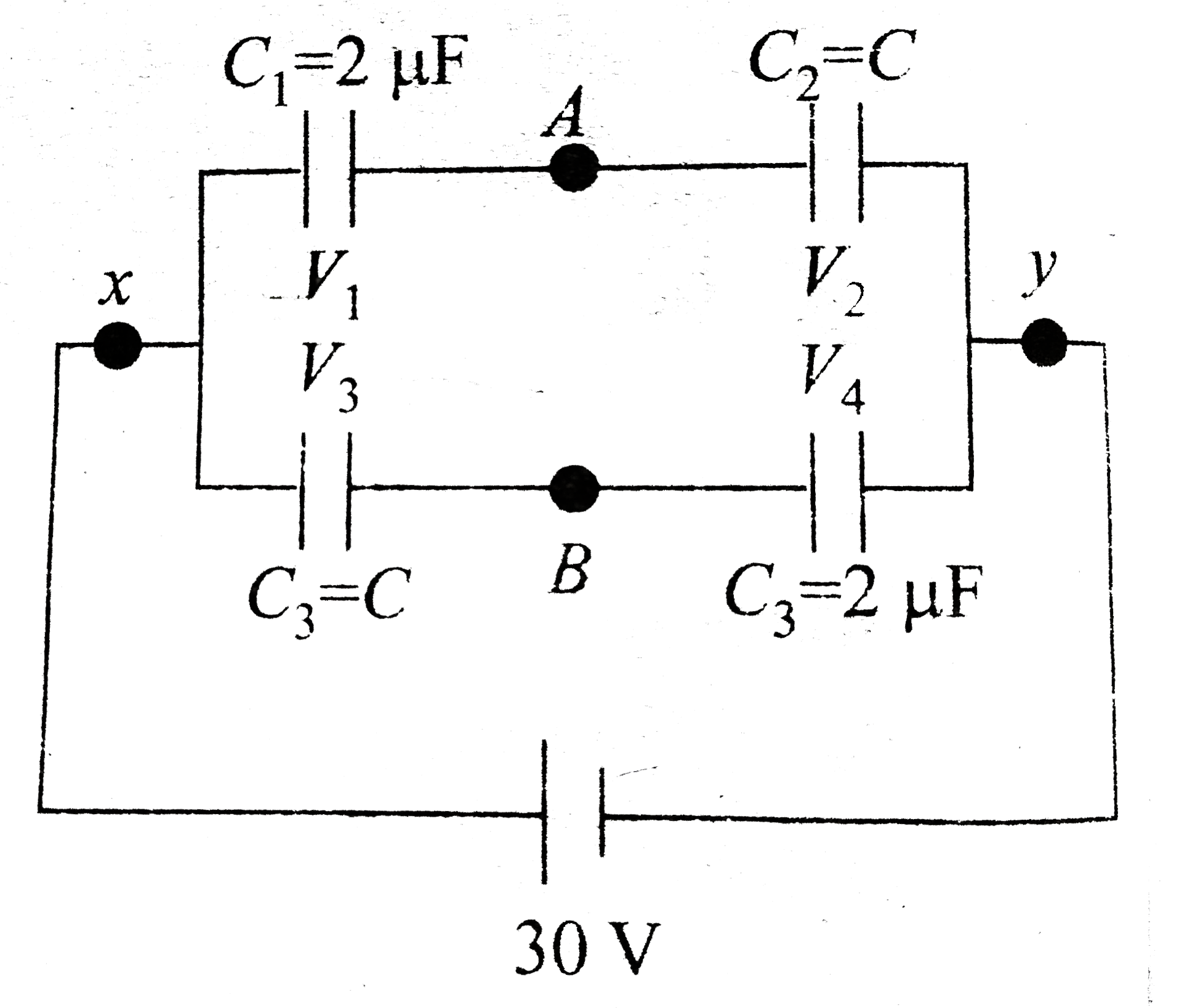
The given circuit shows an arrangement of four capacitors. A potential difference 30V is applied across the combination. It is observed that potentials at connected between A and B differ by 5V. Also if a conducting wire is connected between A and B, electrons will flow from A to B. Of course, we have bot actually connected any wire between AandB, we have described only an if situation. Answer the following question.
 .
.
Equivalent capacitor between x and y is.
2.34μF
1.54μF
1.22μF
0.77μF
The correct Answer is:A
Potential differnce across C4 is V4. As discussed above
V4=V1
V4=17.5V
Consider any branch say, XAY
Since C1 and C2 are in series, charge on C2 is also 35μC.
Using Q=CV for C2
C2=C=35V2=3512.5=2.8μF
Equivalent capacitance of branch XAY is the series equivalent of C3=C=2.8μF and C4=2μF i.e., 1.17μF. There branches are in parallel between X and Y, Hence equivalent capacitance between X and Y is 1.17+1.17=2.34μF.
Capacitor C5 is connected in the part of circuit between X and A either in series or parallel with C1=2μF. Let the equivalent capacitance of C1 and C5, i.e., the equivalent capacitance between X and A be C'1.
Capacitor C6 is connected between A and B Obviously, the circuit then becomes a Wheatstone bridge. Further, since equivalent capacitance between X and Y is independent of the value of C6, it implies that bridge is in the balanced condition and potentials at A and B are now equal, so that
C'1C3=C2C4 or C'12.8=2.82 (C2=2.8μF, as or determined earlier)
or C1=3.92μF
C'1 is the equivalent capacitance of C1=2μF and C5, Since C'1>C1, we can conclude that C1 and C5 are in parallel, So each individual capacitance .Hence, C1 and C5 are in parallel, so
C'1=C1+C5 or C5=C'1−C1=3.92−2=1.92μf
V'1+V2=30
 .
.
 .
.
Since the bridge is in a balanced condition, A and B at same potential and C6 has zero charge. C'1 and C2 are in series. Therfore, charge on C'1 and C2 has the same value, so that potential differnce will be in the inverse ratio of capacitance
[Q=CV or V=QChence for sameQ,V∝1C']
V'1V'2=2.83.92≈0.71 or V'1=0.71V2
From Eq. (iv), 0.71V2+V2=30 or V2=17.5V
Hence V'1=30−V2=12.5V
Since C'1, is parallel equivalet of C1 and C5, so potential differnce across each is V'1=12.5V.
Hence, charge on C5 is
C5V'1=1.92×12.5=24μC.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Multile Correct
11 Videos
- ATOMSBOOK - CENGAGE PHYSICSCHAPTER - ATOMSEXERCISE - QUESTION BANK
40 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
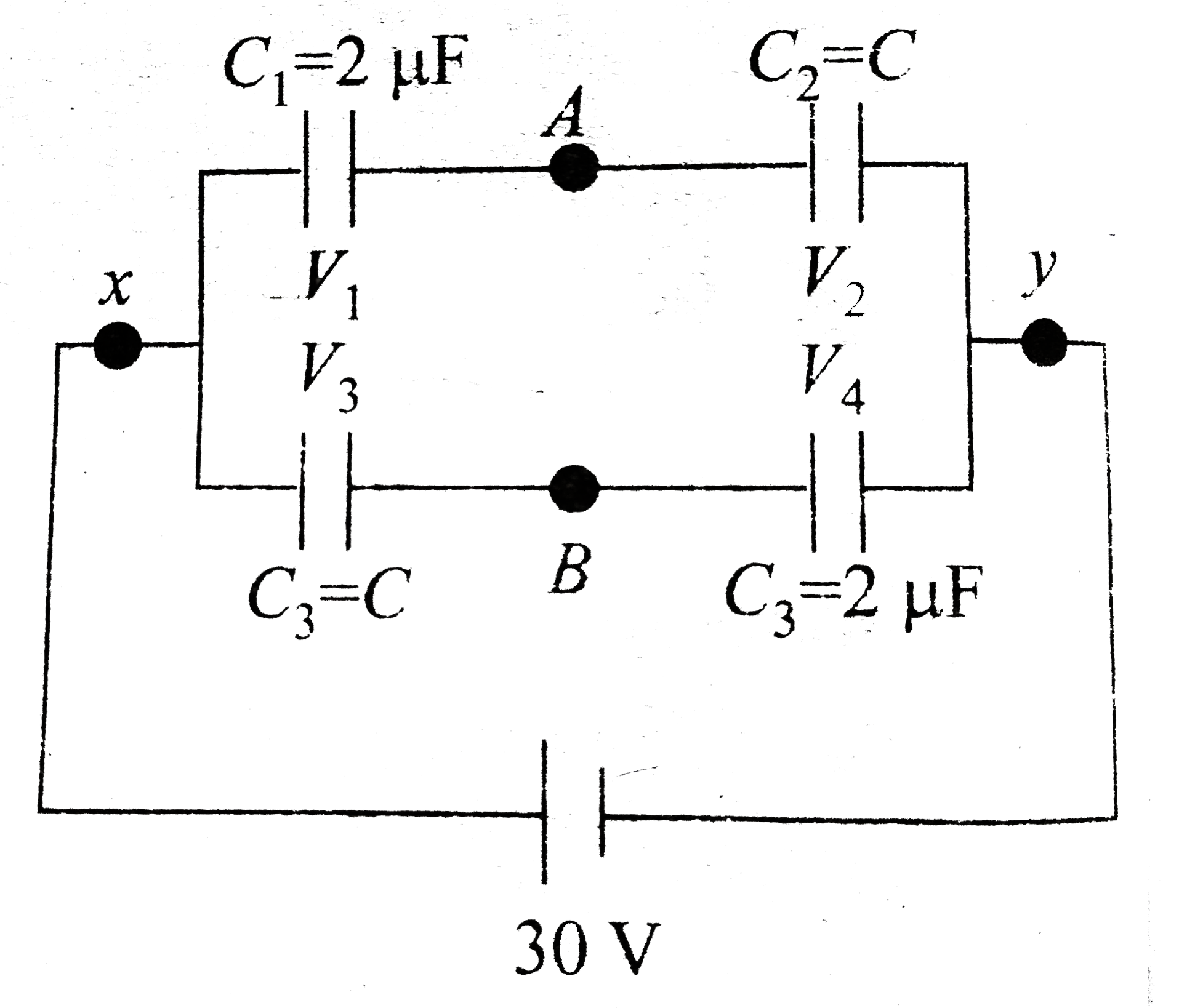
The given circuit shows an arrangement of four capacitors. A potential differnce 30V is applied across the combination. It is observed that potentials at connected between A an B differ by 5V. Also if a conducting wire is connected between A and B, electrons will flow from A→B. Of course, we have bot actually connected any wire between A and B, we have described only an if situation. Answer the following question.
 .
.
Charge on capacitor C1 is.
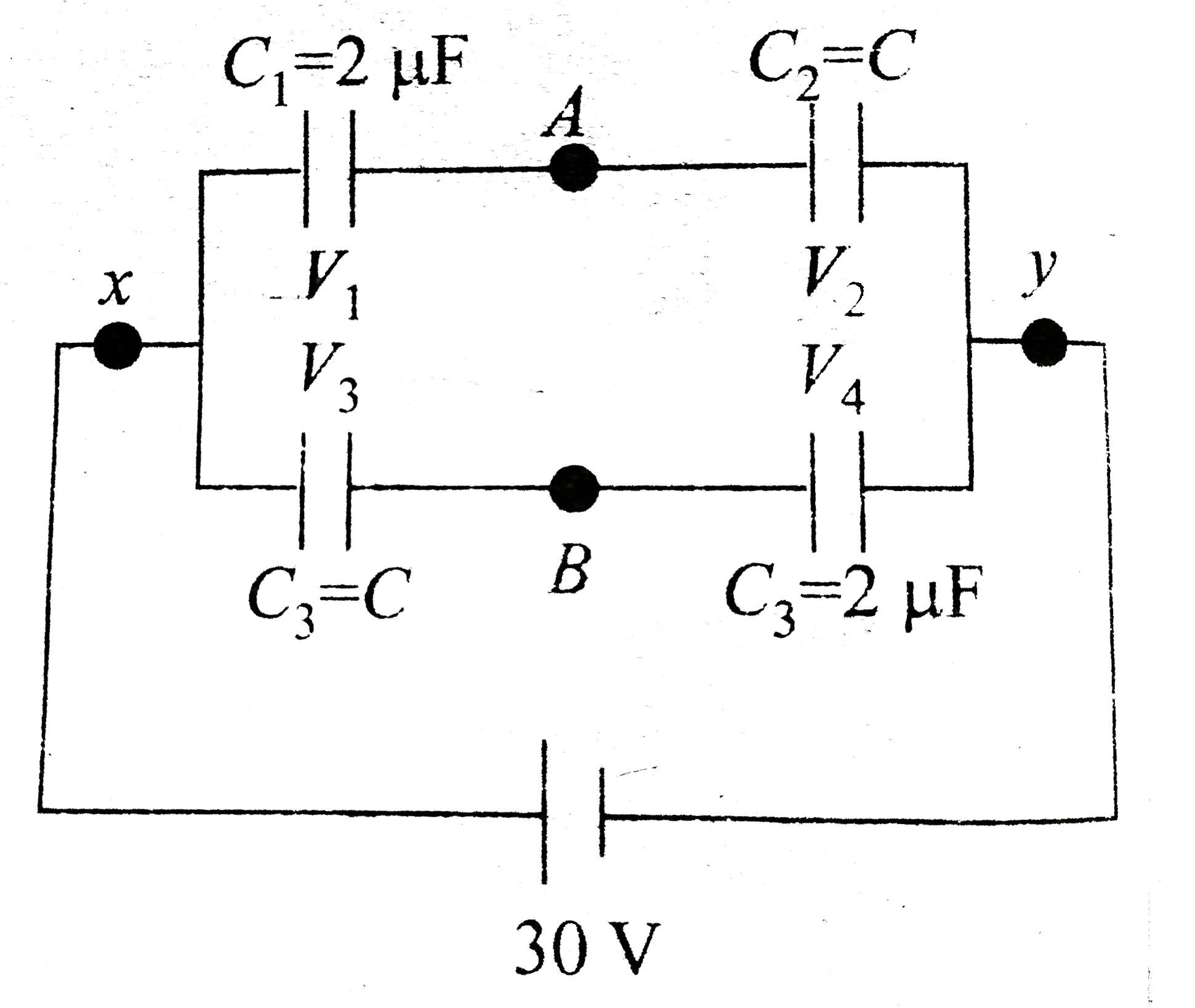
View SolutionThe given circuit shows an arrangement of four capacitors. A potential differnce 30V is applied across the combination. It is observed that potentials at connected between AandB differ by 5V. Also if a conducting wire is connected between AandB, electrons will flow from A to B. Of course, we have bot actually connected any wire between AandB, we have described only an if situation. Answer the following question.
 .
.
Potential differnce across C4 is.
View Solution
Knowledge Check
The given circuit shows an arrangement of four capacitors. A potential difference 30V is applied across the combination. It is observed that potentials at connected between A and B differ by 5V. Also if a conducting wire is connected between A and B, electrons will flow from A→B. Of course, we have bot actually connected any wire between A and B, we have described only an if situation. Answer the following question.
 .
.
Charge on capacitor C1 is.A60μCB52μCC42μCD35μCThe given circuit shows an arrangement of four capacitors. A potential difference 30V is applied across the combination. It is observed that potentials at connected between AandB differ by 5V. Also if a conducting wire is connected between AandB, electrons will flow from A to B. Of course, we have bot actually connected any wire between AandB, we have described only an if situation. Answer the following question.
 .
.
Potential difference across C4 is.A12.5VB15.5VC17.5VD22.5VIn the circuit shown if a conducting wire is connected between points A and B, the current in this wire will :-
 AFlow from A to BBFlow in the direction which will be decided by th value of VCBe zeroDFlow from B to A
AFlow from A to BBFlow in the direction which will be decided by th value of VCBe zeroDFlow from B to A
In the circuit shown if a conducting wire is connected between points A and B, the current in this wire will :-

View SolutionIn the circuit shown if a conducting wire is connected between points A and B, the current in this wire will :-
View SolutionIn the circuit of a condacting wire is connected between point A and B the current is this wire will
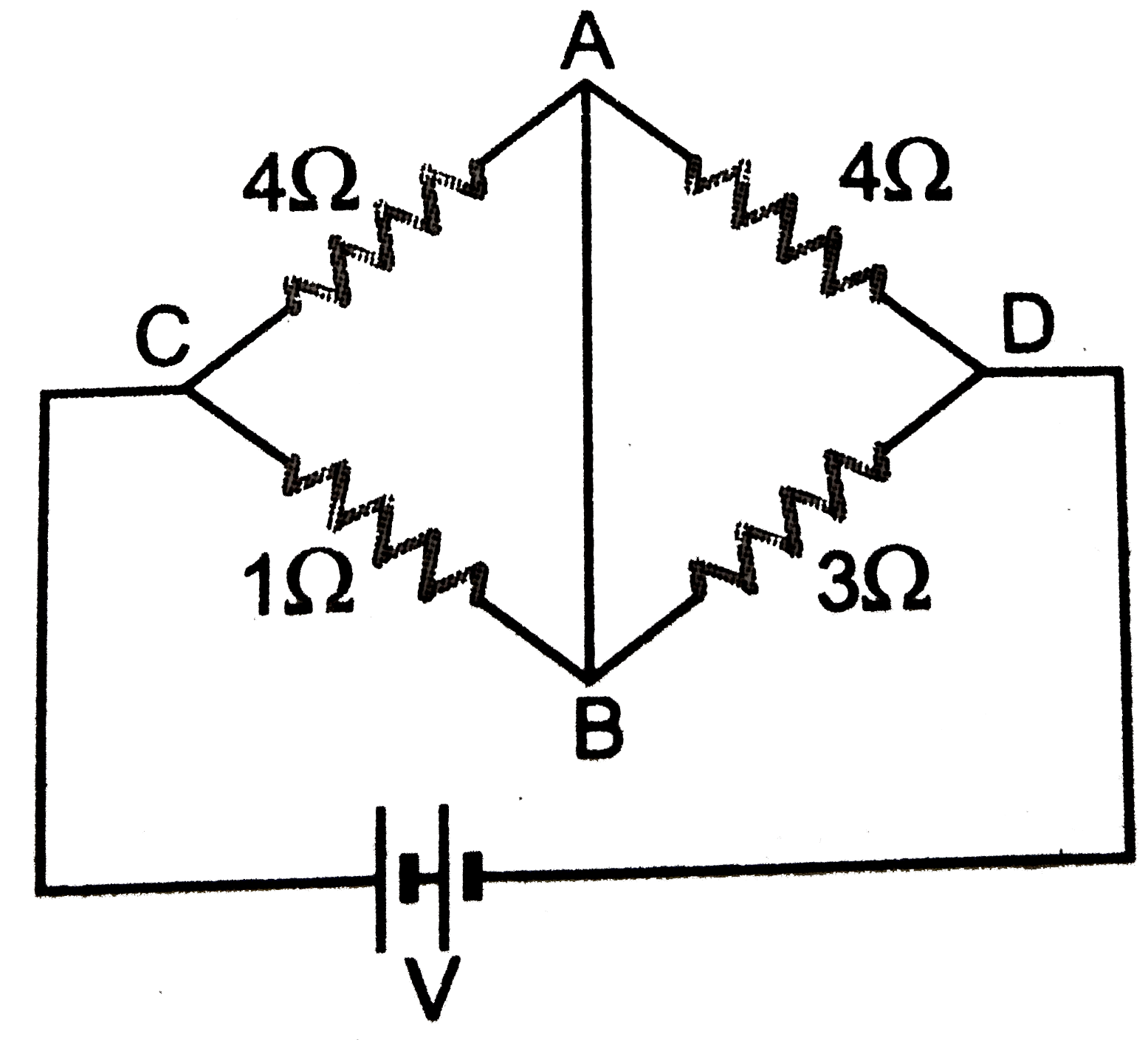
View SolutionIn the circuit shown if a conducting wire is connected between points A and B, the current in this wire will :-

View SolutionIn the circuit shown, the potential difference across the 3μF capacitor is V and the equivalent capacitance between A and B is C Then:
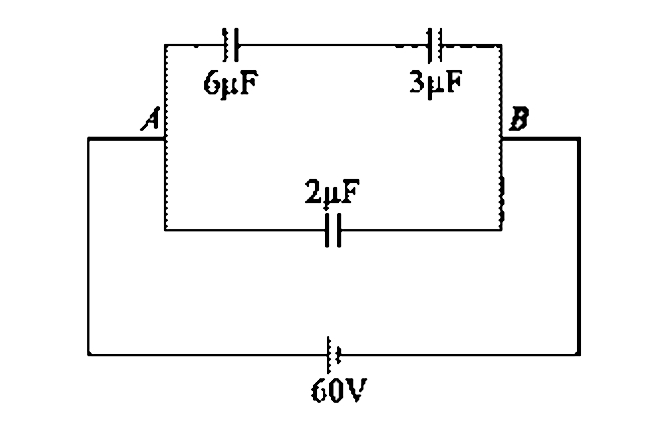
View Solution
