A capacitor of capacitance C has charge Q. it is connected to an identical capacitor through a resistance. The heat produced in the resistance is

A

$\frac{Q^{2}}{2 C}$

B

$\frac{Q^{2}}{4 C}$

C

$\frac{Q^{2}}{8 C}$

D

dependent on the value of the resistance

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

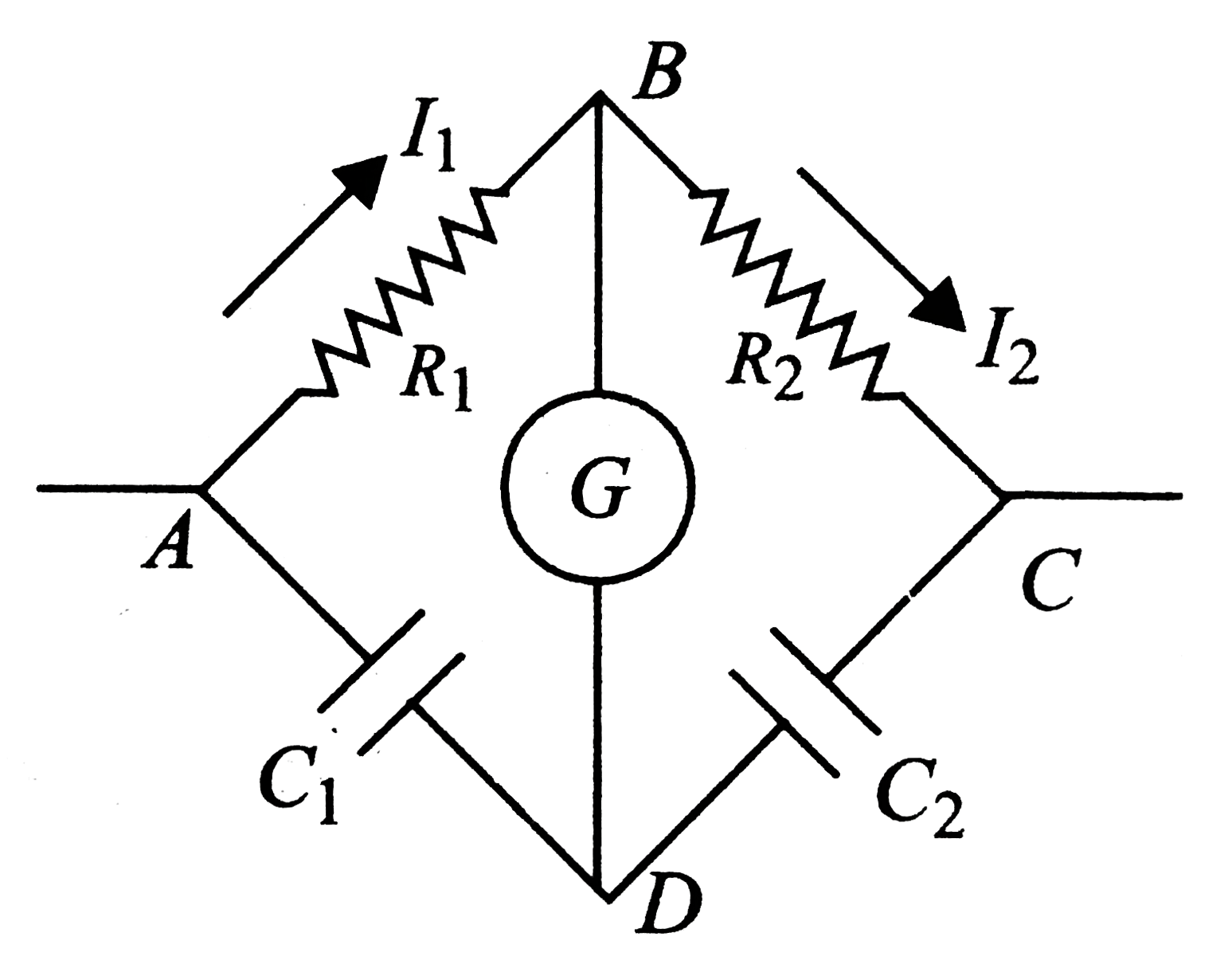
In the steady state, no current is passing throughl the capacitor.
Let the charge on each capacitor be q. Since the current through galvanometer is zero,
$I_{1} = I_{2}$
The potential difference between the ends of the galvnometer
will be zero. Therfore
$V_{A} - V_{B} V_{A} - V_{D}$
$I_{1} R_{2} = \frac{q}{C_{1}} (i)$
Similarly, $V_{B} - V_{C} = V_{D} - V_{C}$
$I_{2} R_{2} = \frac{q}{C_{2}} (i i)$
Dividing Eq. (i) by Eq. (ii) we get
$\frac{I_{1} R_{1}}{I_{2} R_{2}} = \frac{q / C_{1}}{q / C_{2}} = \frac{C_{2}}{C_{1}} or \frac{C_{1}}{C_{2}} = \frac{R_{2}}{R_{1}}$

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A $4 μ F$ capacitor is charged to 400 V. If its plates are joined through a resistance of $2 k Ω$ , then heat produced in the resistance is
A0.16 J
B0.32 J
C0.64 J
D1.28 J
Question 2 - Select One
A $4 μ F$ capacitor is charged to 400 V. If its plates are joined through a resistance of $4 k Ω$ , then heat produced in the resistance will be
A0.16 J
B0.32 J
C0.64 J
D1.28 J
Question 3 - Select One
A capacitor of capacitance C is allowed to discharge through a resistance R. The net charge flown through resistance during one time constant is ( $I_{0}$ is the maximum current)
A $C R l_{0} (\frac{1}{e} + 1)$
B $C R l_{0} (1 - \frac{1}{e})$
C $C R l_{0}$
D $\frac{C R l_{0}}{e}$

CENGAGE PHYSICS-ELECTRIC CURRENT AND CIRCUIT-Single Correct

Home
Ask Doubt
Profile