A cell of internal resistances r is connected to a load of resistance R . Energy is dissipated in the load, but some thermal energy is also wasted in the cell. The efficiency of such an arrangement is found from the expression
( Energy dissipated in the load )/( Energy dissipated in the complete circuit)
Which of the following gives the efficiency in this case?
rR
Rr
rR+r
RR+r
The correct Answer is:D
To find the efficiency of a cell connected to a load resistance, we can follow these steps:
Step 1: Understand the Circuit
We have a cell with an internal resistance r connected to a load resistance R. The current I flowing through the circuit can be calculated using Ohm's law.
Step 2: Calculate the Current
The total resistance in the circuit is the sum of the internal resistance and the load resistance:
Rtotal=R+r
Using Ohm's law, the current I flowing through the circuit is given by:
I=ER+r
where E is the electromotive force (emf) of the cell.
Step 3: Calculate the Heat Dissipated in the Load
The heat HR dissipated in the load resistance R can be calculated using the formula:
HR=I2R
Substituting the expression for current:
HR=(ER+r)2R=E2R(R+r)2
Step 4: Calculate the Total Heat Produced
The total heat Htotal produced in the circuit includes the heat dissipated in both the load and the internal resistance:
Htotal=HR+Hr
where Hr is the heat dissipated in the internal resistance r:
Hr=I2r=(ER+r)2r=E2r(R+r)2
Thus,
Htotal=E2R(R+r)2+E2r(R+r)2=E2(R+r)(R+r)2
Step 5: Calculate the Efficiency
Efficiency η is defined as the ratio of the energy dissipated in the load to the total energy dissipated in the circuit:
η=HRHtotal=E2R(R+r)2E2(R+r)(R+r)2=RR+r
Conclusion
The efficiency of the arrangement is given by:
η=RR+r
We have a cell with an internal resistance r connected to a load resistance R. The current I flowing through the circuit can be calculated using Ohm's law.
The total resistance in the circuit is the sum of the internal resistance and the load resistance:
Rtotal=R+r
Using Ohm's law, the current I flowing through the circuit is given by:
I=ER+r
where E is the electromotive force (emf) of the cell.
The heat HR dissipated in the load resistance R can be calculated using the formula:
HR=I2R
Substituting the expression for current:
HR=(ER+r)2R=E2R(R+r)2
The total heat Htotal produced in the circuit includes the heat dissipated in both the load and the internal resistance:
Htotal=HR+Hr
where Hr is the heat dissipated in the internal resistance r:
Hr=I2r=(ER+r)2r=E2r(R+r)2
Thus,
Htotal=E2R(R+r)2+E2r(R+r)2=E2(R+r)(R+r)2
Efficiency η is defined as the ratio of the energy dissipated in the load to the total energy dissipated in the circuit:
η=HRHtotal=E2R(R+r)2E2(R+r)(R+r)2=RR+r
The efficiency of the arrangement is given by:
η=RR+r
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Multiple Correct
5 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning
6 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective
8 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Concept Based
9 Videos
Similar Questions
If a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P ) vs load resistance ( R ) graph.
View Solution
Knowledge Check
A cell of emf 16V and internal resistant 4Ω can deliver maximum power to a load of resistance R where R is equal to
A2ΩB16ΩC4ΩD8ΩIn a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0A cell of emf 'E' and internal resistance 'r' is connected to a variable external resistor 'R'. The graph which gives the terminal voltage of cell 'V' with respect to R is :
A B
B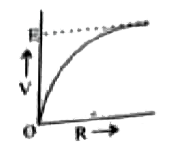 C
C D
D
Find the potential difference across each cell and the rate of energy dissipated in R
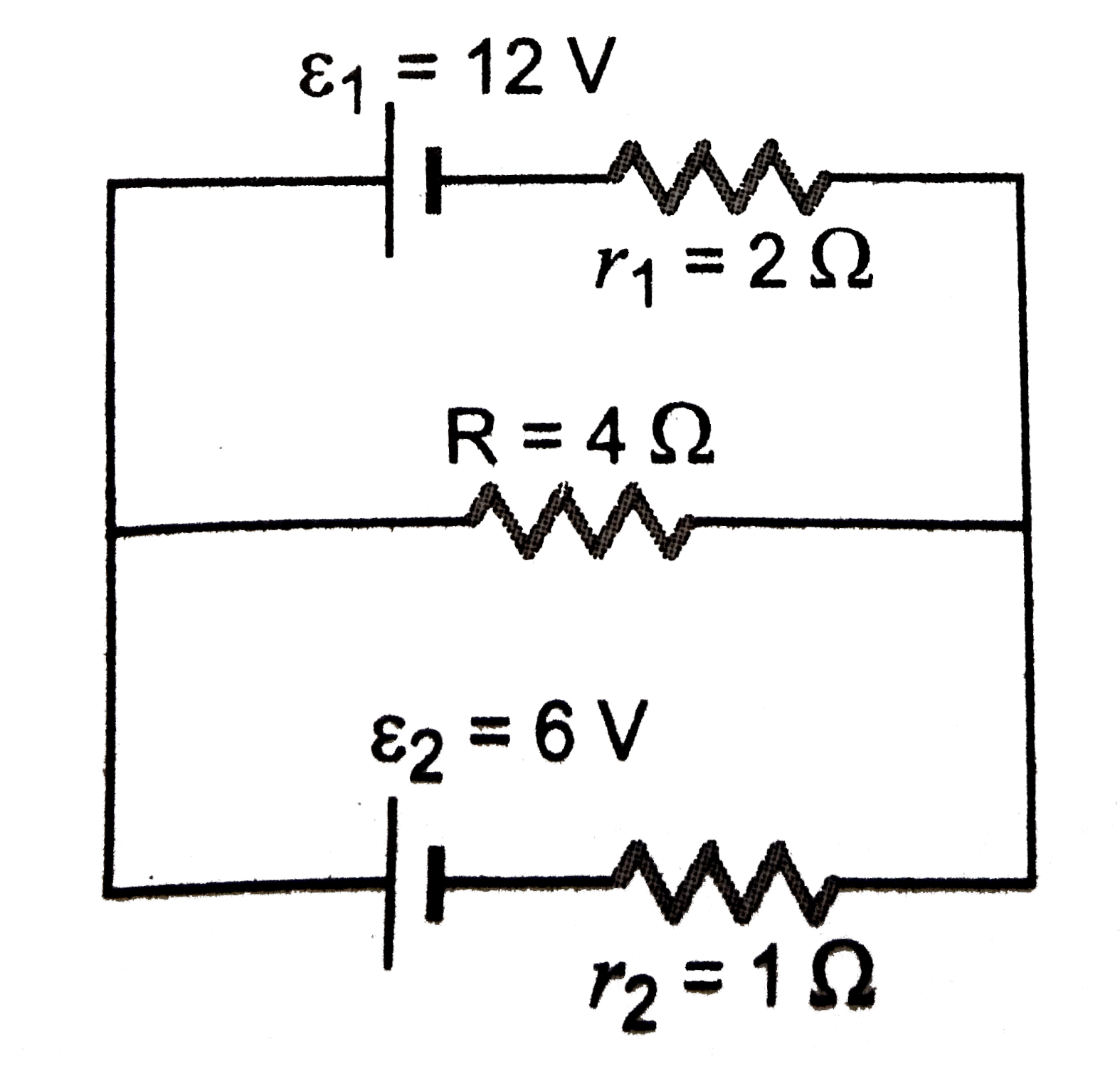
View SolutionA dry cell of emf 1.6V and internal resistance of 0.10Ω is connected to a resistor of resistance Rω. If the current drawn the cell is 2A, then (i) What is the voltage drop across R ? (ii) What is the rate of energy dissipation in the resistor ?
View SolutionA cell of emf ε and internal resistance r is connected across a variable load resistance R. It is found that when R=4Ω the current is 1A and when R is increased to 9Ω, the current reduces to 0.5A. Find the value of the emf ε and internal resistancer
View SolutionAn inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
View SolutionAn inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
View Solution
