Question

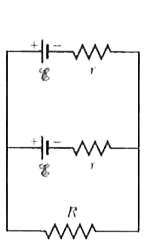
Two cells , each of $emfE$ and internal resistance $r$, are connected in parallel across a resistor $R$. The power delivered to the resistor is maximum if $R$ is equal to

Options

A. ` r // 2`
B. `r`
C. ` 2r`
D. `0`

Answer

A

Explanation

To solve the problem, we need to find the value of the load resistance $$R$$ that maximizes the power delivered to it when two cells, each with an emf $$E$$ and internal resistance $$r$$, are connected in parallel.

1. Understanding the Circuit Configuration:
- We have two cells connected in parallel, each with an emf \( E \) and internal resistance \( r \).
- These cells are connected across a load resistor \( R \).

2. Calculate the Equivalent Internal Resistance:
- When two resistances are connected in parallel, the equivalent resistance \( R_{\text{internal}} \) can be calculated using the formula:
\( R_{\text{internal}} = \frac{r \cdot r}{r + r} = \frac{r^2}{2r} = \frac{r}{2} \)
- Therefore, the equivalent internal resistance of the two cells in parallel is \( \frac{r}{2} \).

3. Applying the Maximum Power Transfer Theorem:
- According to the maximum power transfer theorem, maximum power is delivered to the load when the load resistance \( R \) is equal to the internal resistance of the source.
- Thus, we set:
\( R = R_{\text{internal}} \)
- Substituting the value of \( R_{\text{internal}} \):
\( R = \frac{r}{2} \)

4. Conclusion:
- The power delivered to the resistor \( R \) is maximum when:
\( R = \frac{r}{2} \)

Final Answer:
The power delivered to the resistor is maximum if \( R \) is equal to \( \frac{r}{2} \).

---