The corners A, B, C, and D of a square are occupied by charges , and Q, respectively. The side of square is 2b. The field at the midpoint of side CD is zero. What is the value of ?
The correct Answer is:A
To solve the problem, we need to find the ratio qQ given that the electric field at the midpoint of side CD of a square is zero. The square has charges q at A, −q at B, 2Q at C, and Q at D, and the side length of the square is 2b.
1. Identify the Setup:
- Place the square in a coordinate system:
- A at (0,2b)
- B at (0,0)
- C at (2b,2b)
- D at (2b,0)
- The midpoint of side CD is at (2b,b).
2. Calculate the Electric Field Contributions:
- The electric field →E at the midpoint due to each charge can be calculated using Coulomb's law:
→E=kqr2^r
- Here, k is Coulomb's constant, r is the distance from the charge to the point of interest, and ^r is the unit vector pointing from the charge to the point.
3. Electric Field Due to Charge at A (q):
- Distance from A to midpoint = √(2b−0)2+(b−2b)2=√4b2+b2=√5b2=b√5
- The electric field →EA at the midpoint due to charge q:
EA=kq(b√5)2=kq5b2
- Direction: towards the midpoint (downwards).
4. Electric Field Due to Charge at B (-q):
- Distance from B to midpoint = √(2b−0)2+(b−0)2=√4b2+b2=√5b2=b√5
- The electric field →EB at the midpoint due to charge −q:
EB=k−q(b√5)2=−kq5b2
- Direction: away from the midpoint (upwards).
5. Electric Field Due to Charge at C (2Q):
- Distance from C to midpoint = b (directly down).
- The electric field →EC at the midpoint due to charge 2Q:
EC=k2Qb2
- Direction: downwards.
6. Electric Field Due to Charge at D (Q):
- Distance from D to midpoint = b (directly up).
- The electric field →ED at the midpoint due to charge Q:
ED=kQb2
- Direction: upwards.
7. Set Up the Equation for Zero Electric Field:
- The total electric field at the midpoint is the sum of the contributions:
EA+EB+EC+ED=0
- Substitute the values:
kq5b2−kq5b2+k2Qb2−kQb2=0
- Simplifying gives:
k(2Q−Qb2)=0
- This simplifies to:
kQb2=0
- Which implies:
2Q−Q+q5−q5=0
8. Solve for the Ratio qQ:
- From the balance of forces, we can equate the magnitudes:
2Q=Q+2q5
- Rearranging gives:
Q=2q5
- Therefore:
qQ=52
Final Answer:
qQ=52
- Place the square in a coordinate system:
- A at (0,2b)
- B at (0,0)
- C at (2b,2b)
- D at (2b,0)
- The midpoint of side CD is at (2b,b).
- The electric field →E at the midpoint due to each charge can be calculated using Coulomb's law:
→E=kqr2^r
- Here, k is Coulomb's constant, r is the distance from the charge to the point of interest, and ^r is the unit vector pointing from the charge to the point.
- Distance from A to midpoint = √(2b−0)2+(b−2b)2=√4b2+b2=√5b2=b√5
- The electric field →EA at the midpoint due to charge q:
EA=kq(b√5)2=kq5b2
- Direction: towards the midpoint (downwards).
- Distance from B to midpoint = √(2b−0)2+(b−0)2=√4b2+b2=√5b2=b√5
- The electric field →EB at the midpoint due to charge −q:
EB=k−q(b√5)2=−kq5b2
- Direction: away from the midpoint (upwards).
- Distance from C to midpoint = b (directly down).
- The electric field →EC at the midpoint due to charge 2Q:
EC=k2Qb2
- Direction: downwards.
- Distance from D to midpoint = b (directly up).
- The electric field →ED at the midpoint due to charge Q:
ED=kQb2
- Direction: upwards.
- The total electric field at the midpoint is the sum of the contributions:
EA+EB+EC+ED=0
- Substitute the values:
kq5b2−kq5b2+k2Qb2−kQb2=0
- Simplifying gives:
k(2Q−Qb2)=0
- This simplifies to:
kQb2=0
- Which implies:
2Q−Q+q5−q5=0
- From the balance of forces, we can equate the magnitudes:
2Q=Q+2q5
- Rearranging gives:
Q=2q5
- Therefore:
qQ=52
qQ=52
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type
109 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Four point charge q,−q,2Q and Q are placed in order at the corners A, B, C and D of a square. If the field at the midpoint of CD is zero then the value of q/Q is 5√5x. Find the value of x.
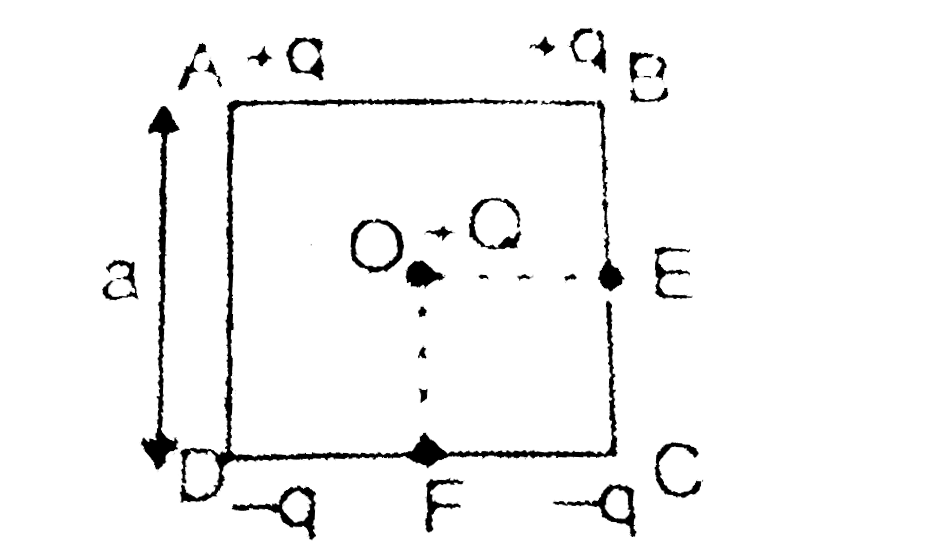
View SolutionFour charges +q, +q, -q, -q are fixed respectively at the corners of A, B, C and D of a square of side 'a' arranged in the given order. Calculate the electric potential and intensity at O (Center of square). If E and F are the midpoints of sides BC, CD respectively, what will be the work done by external agent in carrying a charge Q slowly from O to E and from O to F ?
View Solution
Knowledge Check
Point charges g, -q, 2Q and Q are placed in order at the corners A, B, Cand D of a square of side 2b. If the field at the midpoint of CD is zero, then qQ is
A1B2C2√25D5√52Three charges +q, +q, +2q are arranged as shown in figure. What is the field at point P (center of side AC)
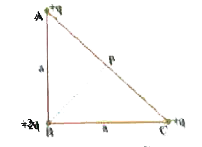 AE=qπε0a2BE=q2πε0a2CE=q3πε0a2DE=q4πε0a2
AE=qπε0a2BE=q2πε0a2CE=q3πε0a2DE=q4πε0a2Four charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The electric potential at O is.A√2qπε0aB√3qπε0aCqπε0aDzero
Four charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The electric field at O is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to F is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to E is.
View SolutionFour charges Q-Q, Q-Q are placed at the corners of a square as shown . The potential is zero at points
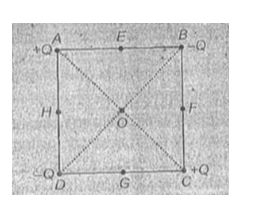
View SolutionCharges +q,−q,+q and −q are placed at the corners A,B,C and D respectively of a square of side a. The potential energy of the system is 1/4πε0 times
View Solution
