In a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.
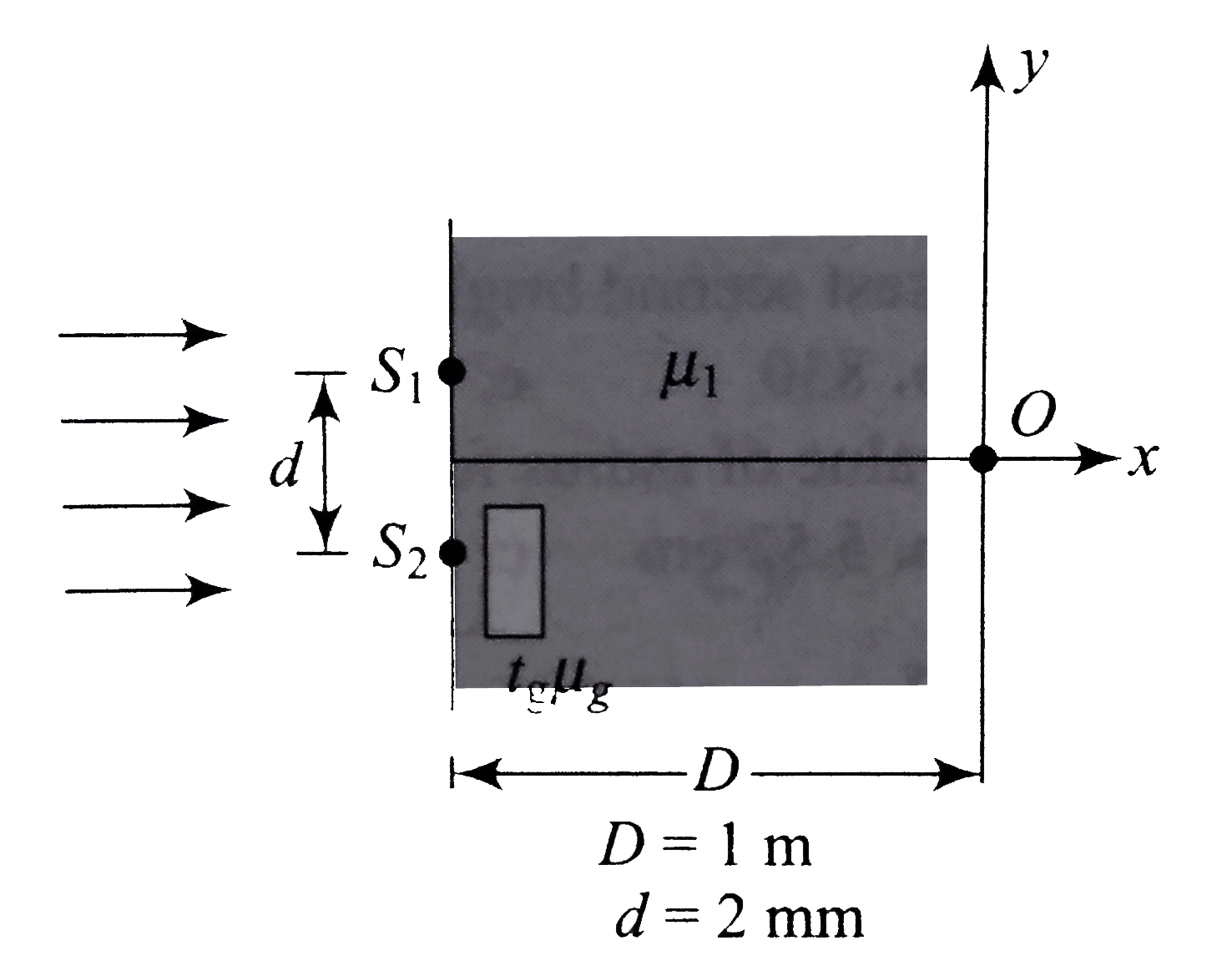
Find the time when central maxima is at point O. located symmetrically on the x-asix.
2 s
4 s
6 s
8 s
The correct Answer is:b
We consider a point P on the screen.
Optical path length,
[S1P]liquid=[μ1S1P]air
[S1P−t]liquid+tglass=μ[S1P−t]air+[μgt]air
=[μ1S2P+(μg−μ1)t]air
Hence, optical path difference at P,
Δx=[μ1S2P+(μg−μ1)t]−μ1S1P
=μ1(S1P−S1P)+(μg+μ1)t
For a point P at the screen in the absence of liquid,
S2P=S1P=ydD
If a liquid is filled,
[S2P−S1P]liquid=μ1ydD
Thus,
Δx=μ1ydD+[μg−μt]t

a. For central maxima,
Δx=0
y=[μg−μ1μ1]tDd=(4−T)tD(10−T)d
At Point O, y=0
Thus, T=4
b. Speed of central maxima,
v=∣∣∣dydt∣∣∣=6Dt(10−T)2d
Central maxima is at O at time t=4 s.
∴v=6Dt36D=1×36×10−66×2×10−3=3×10−3ms−1
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A double slit experiment is performed with light of wavelength 500 nm A thin film of thickness 2 μm and refractive index 1.5 is introduced in the path of the upper beam the location of the central maximum will
View SolutionA double slit experiment is performed with light of wavelength 500 nm A thin film of thickness 2 μm and refractive index 1.5 is introduced in the path of the upper beam the location of the central maximum will
View Solution
Knowledge Check
In a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.

What is the speed of the central maxima when it is atA3×10−3ms−1B4×10−3ms−1C6×10−3ms−1D1×10−3ms−1In YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
Aλ(2μ−1)B2λ(2μ−1)Cλ(μ−1)D2λ(2μ+1)In the Young's double slit experiment , a mica slip of thickness t and refractive index μ is introduced in the ray from first source S1 . By how much distance fringes pattern will be displaced ? (d = distance between the slits and D is the distance between slits and screen)
AdD(μ−1)tBDd(μ−1)tCd(μ−1)DDDt(μ−1)
In YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
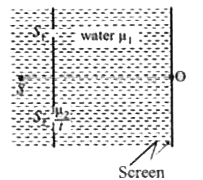
View SolutionA YDSE is conducted in water (μ1) as shown in figure. A glass plate of thickness t and refractive index μ2 is placed in the path of S2. The optical path difference at O is
View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View SolutionLight travels through a glass plate of thickness t and refractive index μ. If c is the speed of light in vacuum, the time taken by light to travel this thickness of glass is
View SolutionIn a young's double slit experiment ,let Aand B be the two slits.A thin film film of thickness t and refractive indexμ is pklaced in front of A.Let β =fringe width.The central maximum will shift:
View Solution
