The minimum value of d os that there is a dark fringe at O is dmin. For the value of dmin, the distance at which the next bright fringe is formed is x. Then
dmin=√λD
dmin=√λD2
x=dmin2
x=dmin
The correct Answer is:b.,d
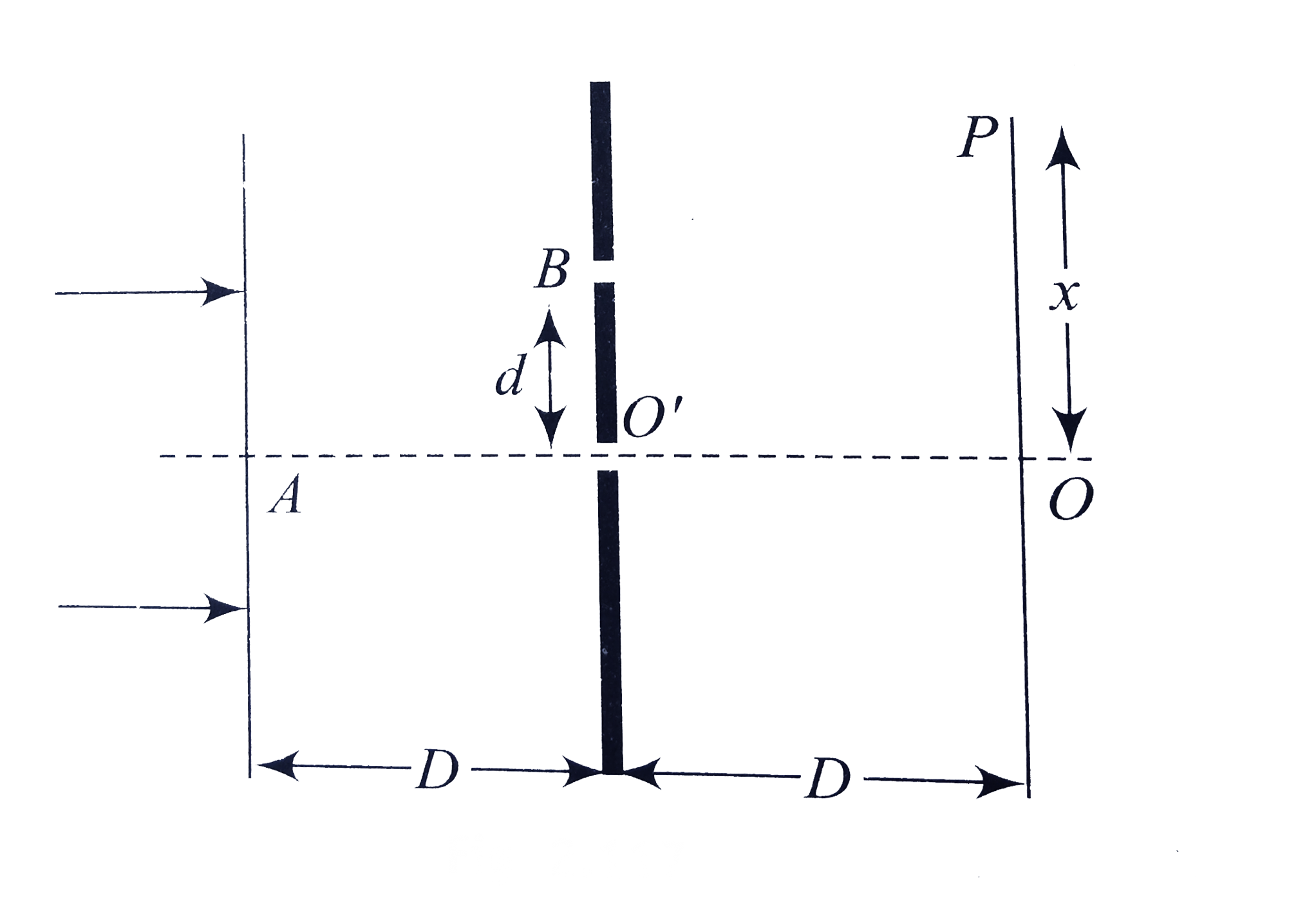
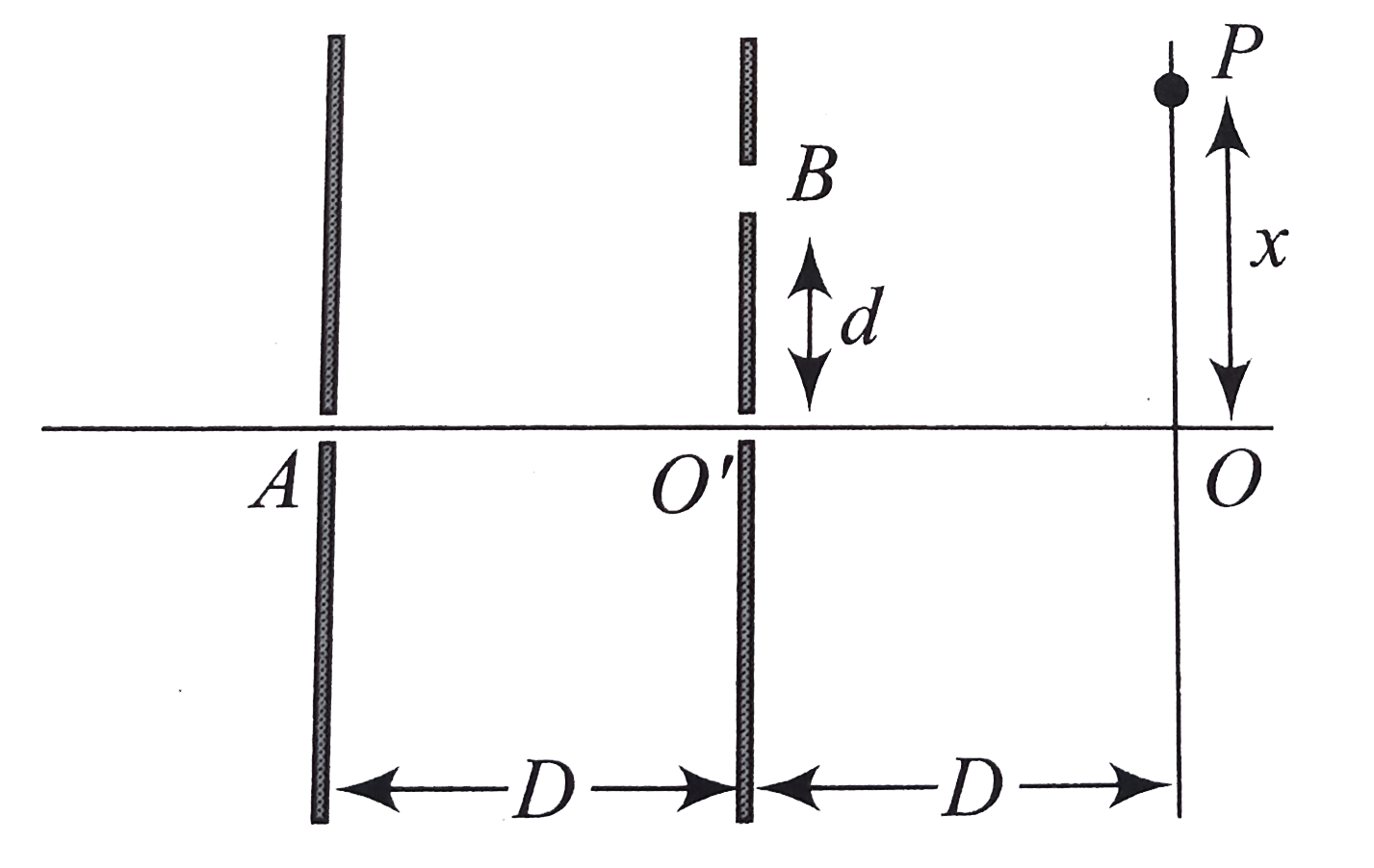
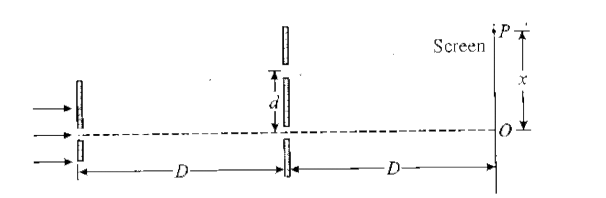
There is a dark fringe at O if the path difference δ=ABO−AO'O=λ2
⇒2√D2−d2−2D=2d22D=D2D=λ2
dmin=√λD2
The bright fringe is formed at P if the path difference
δ=AO'P−ABP=λ
=D+√D2+x2−√D2+d2−√D2+(x−d)2=λ
=x22D−d22D−(s2+d2−2xd)2D=λ
Given d=dmin
On solving, x=dmin=√λD2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Linked Comprehension88videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Single Correct128videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK34videos
THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK38videos
WAVES
Similar Questions
Consider the arrangement shown in figure-6.38. The distance D is large compared to the separation d between the slits.
(a) Find the minimum value of d so that there is a dark fringe at O.
(b) Suppose d has this value. Find the distance x at which the next bright fringe is formed.
(c ) Find the fringe width.
 View Solution
View SolutionConsider the arrangement shown in figure. The distance D is large compared to the searated d between the slits. a. Find the minimum value of d so that there is a dark fringe at O. b. Suppose d has this value. Find the distance x at which the next bright firnnge is formed. c.Find teh fringe width.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the arrangment shown in fin.

Find the distance x at which the next fringe is formed.A3λ2Bλ4Cλ2D5λ2 - Question 2 - Select One
The distance of nth bright fringe to the nth dark fringe in Young's experiment is equal to
A3λD2dB2λDdCλD2dD(λDd) - Question 3 - Select One
In the arrangment shown in fin.

For what minimum value of d is there a dark bant at point O on the screen?A√Dλ4B√3Dλ4C√Dλ8D√2Dλ43
In Young's double slit experiment, the distance between two coherent sources is 1 mm and the distance between the slits and the screen is 1 m. If the 10th dark fringe is at a distance of 4.75 mm from the central bright fringe, calculate
the distance of 5th bright fringe from the central bright fringe.View SolutionIn a biprism experiment, the fringe width is 0.4mm. The distance between the fourthh dark fringe and the sixth bright fringe is
View SolutionIn the double-slit experiment, the distance of the second dark fringe from the central line are 3mm. The distance of the fourth bright fringe from the central line is
View SolutionIn a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
View SolutionIn a double slit experiment , the coherent sources are spaced 2d apart and the screen is placed a distance D from the slits. If nth bright fringe is formed on the screen exactly opposite to a slit , the value of n must be -
View Solution

