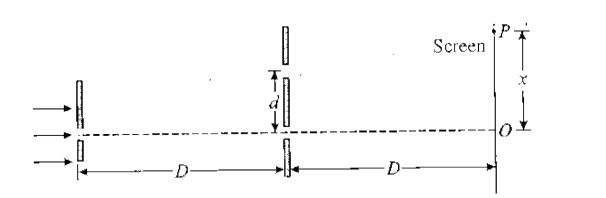
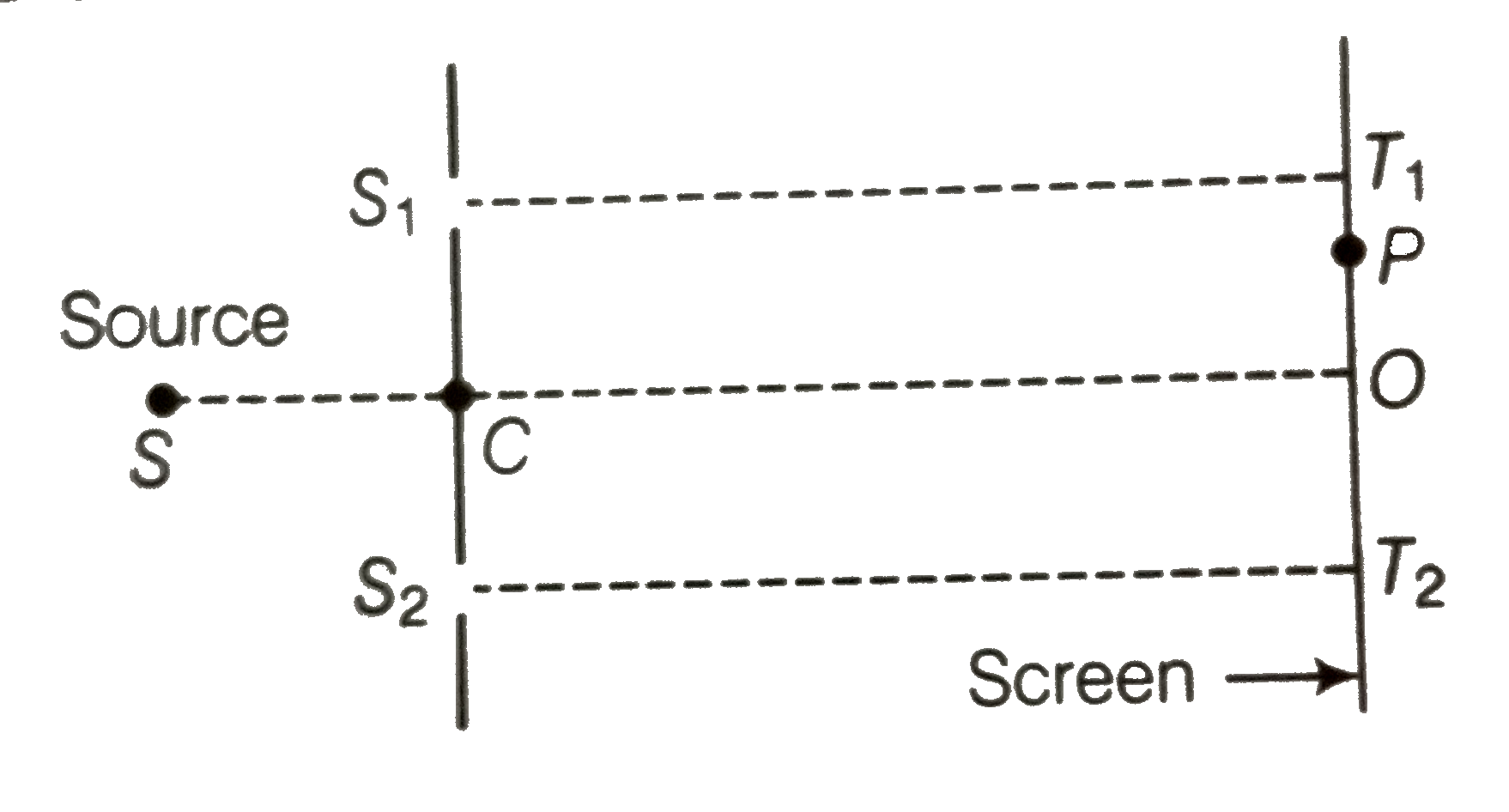
Consider the arrangement shown in figure. The distance D is large compared to the searated d between the slits. a. Find the minimum value of d so that there is a dark fringe at O. b. Suppose d has this value. Find the distance x at which the next bright firnnge is formed. c.Find teh fringe width.

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

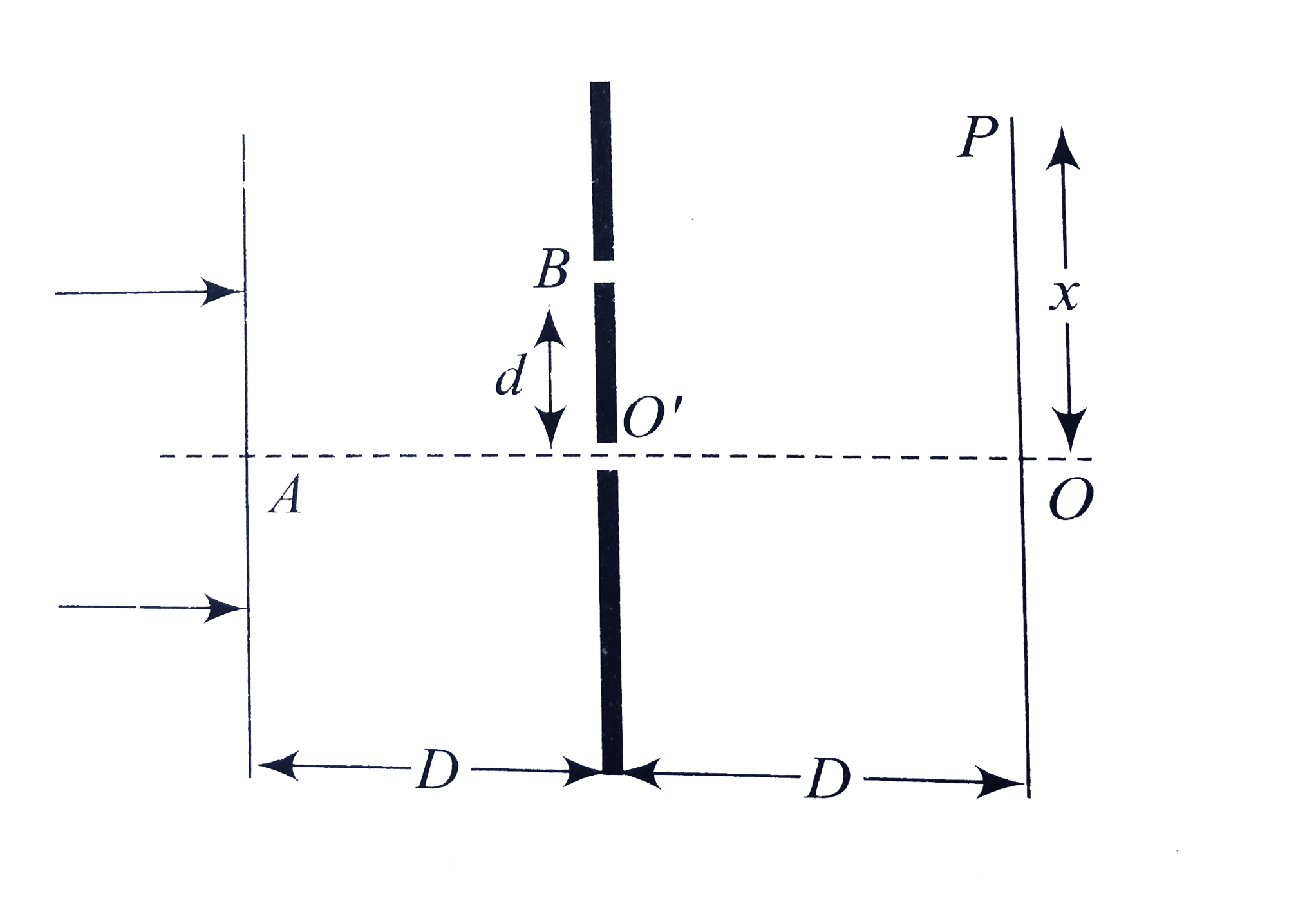
From the diagram it can be seen that at point O,
Path differene $= (A B + B O) - (A C + C O)$
$= 2 (A B - A C)$
[Since AB=BO and AC=CO] $< b r >$ =2(sqrt(D^2+d^2D)) $< b r > F or d a r k \in \geq p a t h d \Leftrightarrow e r e n c e s h o d - - b e o d d μ < i p \leq o f$ lamda/2 $< b r >$ So, 2(sqrt(D^2+d^2-D))=(2n+1)lamda/2 $< b r >$ rarrsqrtD^2+d^2=D+(2n+1)lamda/4 $< b r >$ rarr D^2+d^2=D^2+(2n+1)^2lamda^2/16+(2n+1)(lamdaD)/2 $< b r > N e g \leq c t \in g$ (2n+1)^2lamda^2/16 $a s i t i s v e r y s m a l l w e \geq t$ d=(sqrt2n+1)(lamdaD)/2 $< b r > f or min i μ m d p u \in g n = 0 < b r >$ rarr d_(min)=sqrt(((lamdaD)/2))

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a arrangement shown in the fig.the distance D is latge compared to the separation d between this slits ,find:

The minimum value of d for which there is a dark fringe at the point $O$ .
A $\sqrt{λ D / 2}$
B $\sqrt{D λ / 3}$
C $\sqrt{λ D}$
Dcannot be calcualted
The minimum value of d os that there is a dark fringe at O is $d_{min}$ . For the value of $d_{min}$ , the distance at which the next bright fringe is formed is x. Then

A $d_{min} = \sqrt{λ D}$
B $d_{min} = \sqrt{\frac{λ D}{2}}$
C $x = \frac{d_{min}}{2}$
D $x = d_{min}$
In a arrangement shown in the fig.the distance D is latge compared to the separation d between this slits ,find:

The fringe width is
A $\frac{3 D λ}{4 d}$
B $\frac{3 D λ}{2 d}$
C $\frac{D λ}{d}$
D $\frac{2 D λ}{d}$

HC VERMA-LIGHT WAVES-Exercises

Home
Ask Doubt
Profile