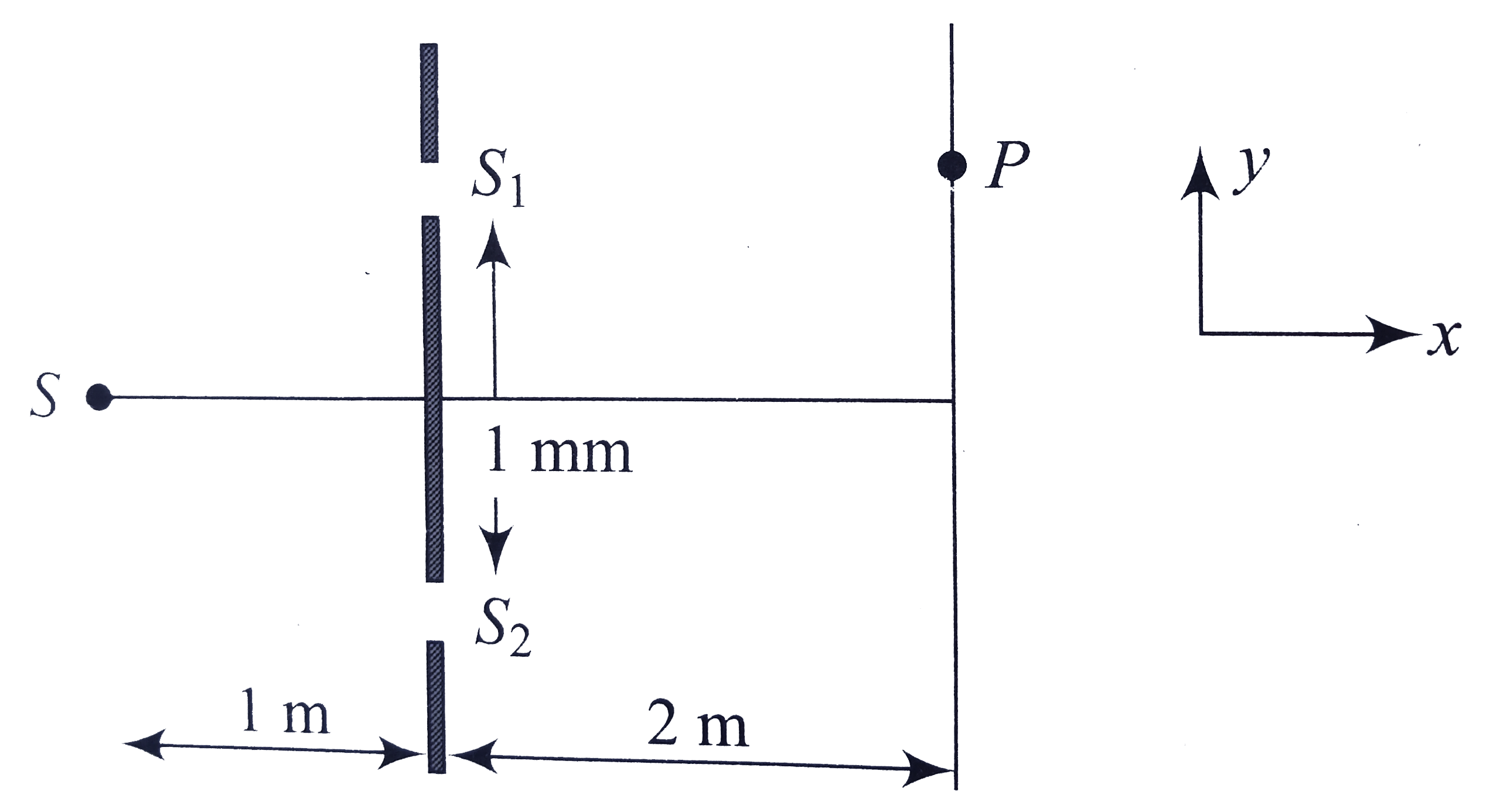
In a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
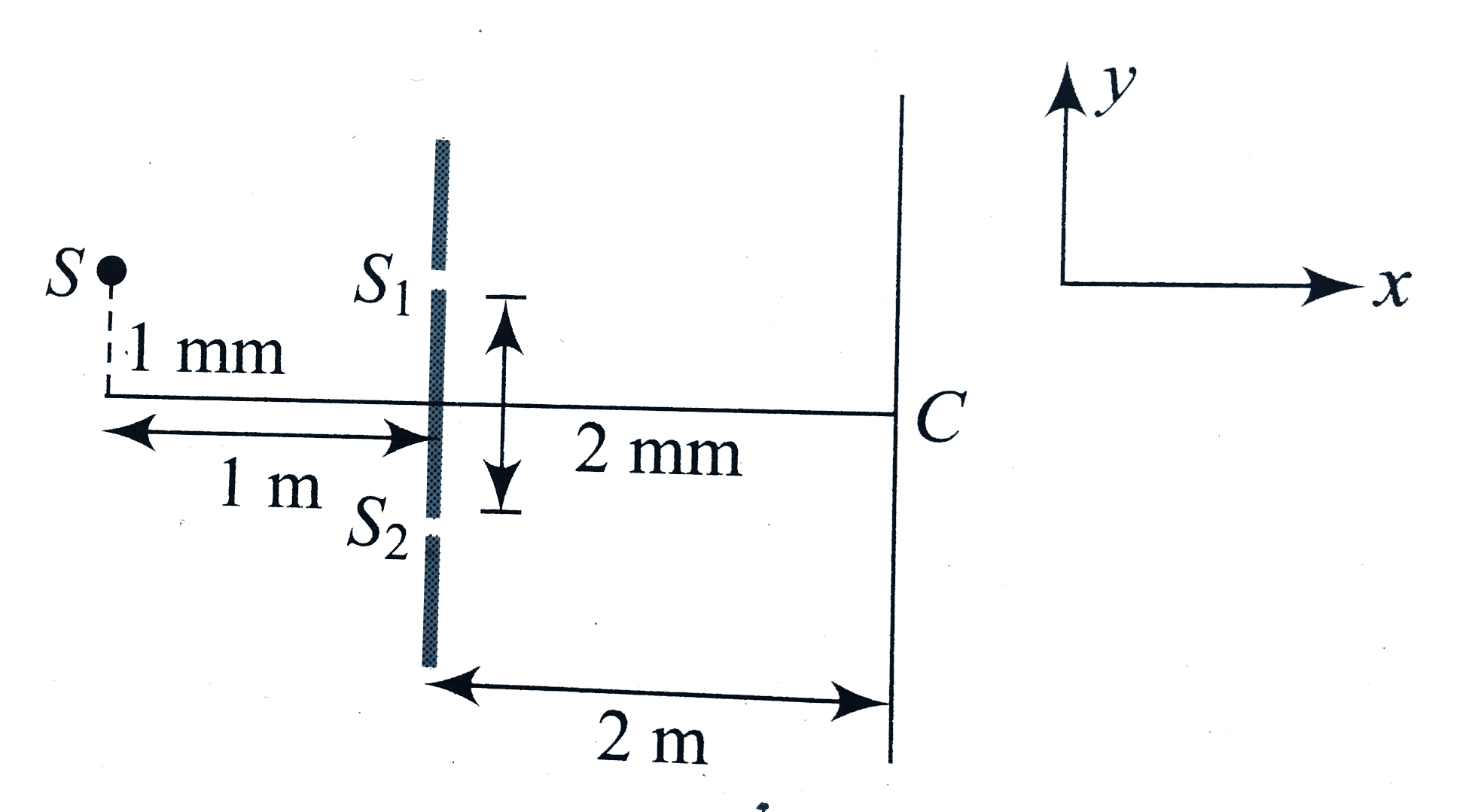
At t=2 s, the position of central maxima is
2 mm above C
2 mm below C
4 mm above C
4 mm below C
The correct Answer is:d
Path difference at any point on the screen Δx=bda+y'dD
For central maixma. Δx=0
⇒y'=−bda=−(1+cosπt)21
y'=−2(1+cosπt)
position of central maxima at any time is
y'=−2(1+conπt) mm
At t=2s,y,'=−4mm.
At t=1 s, central maxima is at y'=0.
But when a plate is inserted central maxima is at
y1=Dd(μ−1)t=1mm

Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
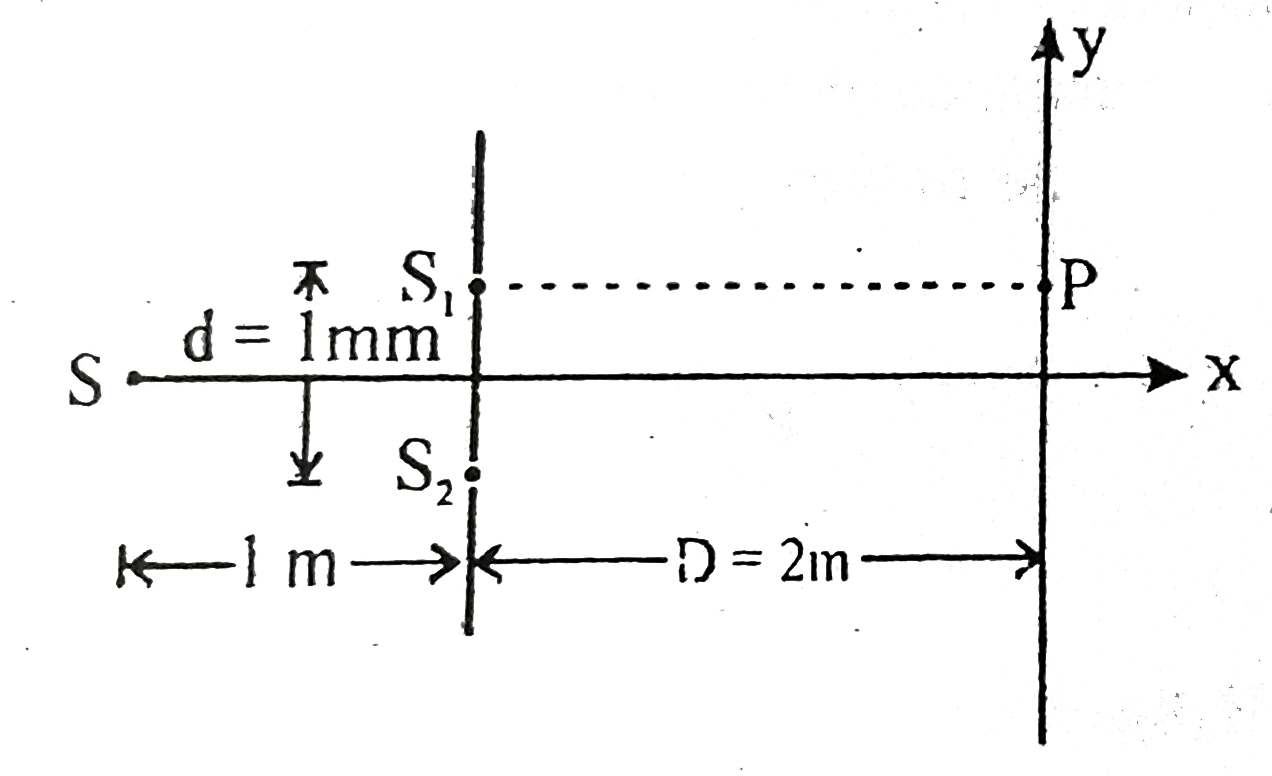
In a modified YDSE the sources S of wavelength 5000 A oscillates about axis of setup according to the equation y=0.5sin(π6)t where y is in millimeter and t in second. At what time ti will the intensity at P, a point exactly in front of slit S1 be maximum for the first time?
View SolutionIn young’s double slit experiment with a source of light of wavelength 6320Å, the first maxima will occur when
View Solution
Knowledge Check
In a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
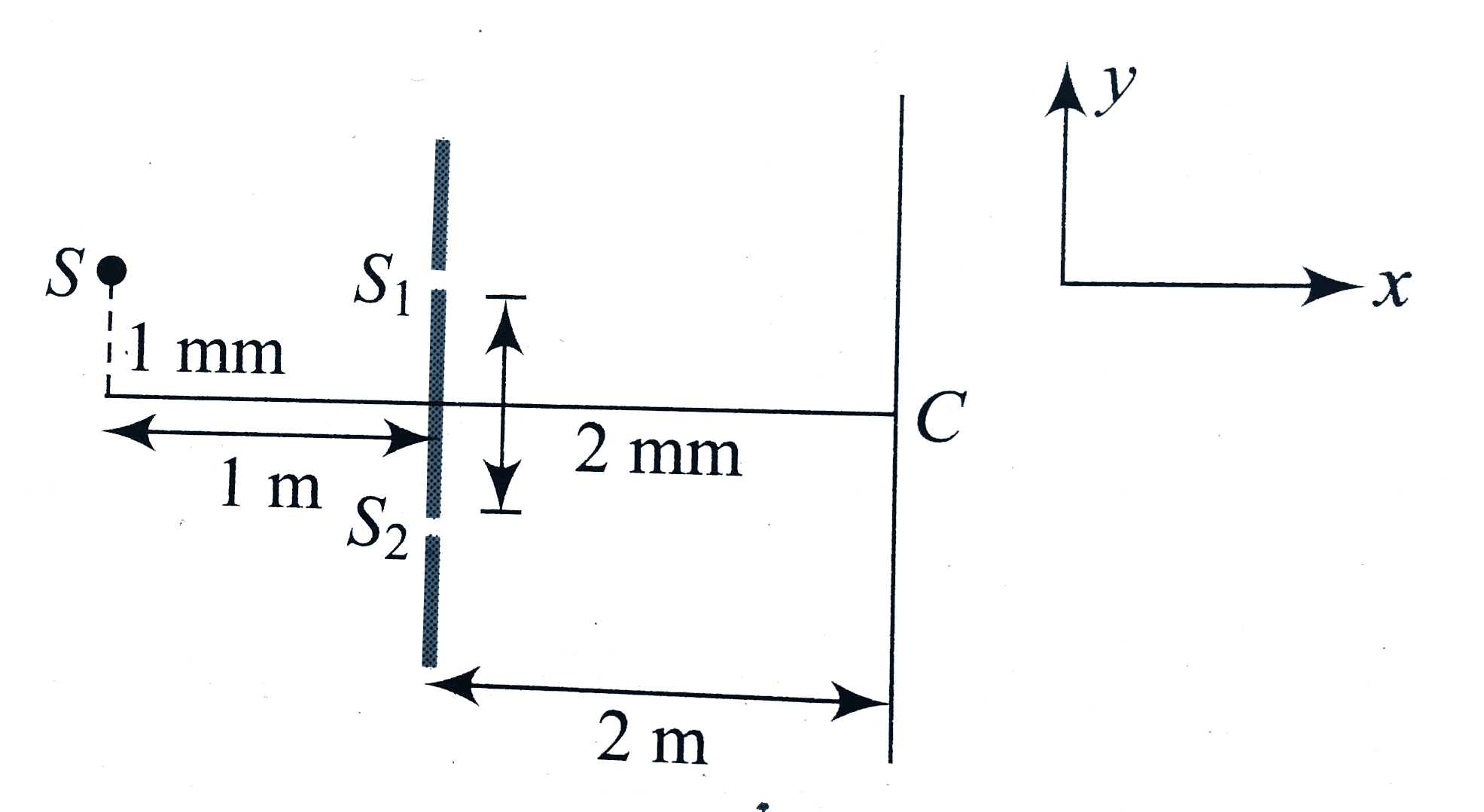
At t=1 s, a slab of thickness 2×10−3mm an refractive index 1.5 is placed just in front of S1. The central maximum is formed atA1 mm above CB1 mm below CC2 mm above CD2 mm below CIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
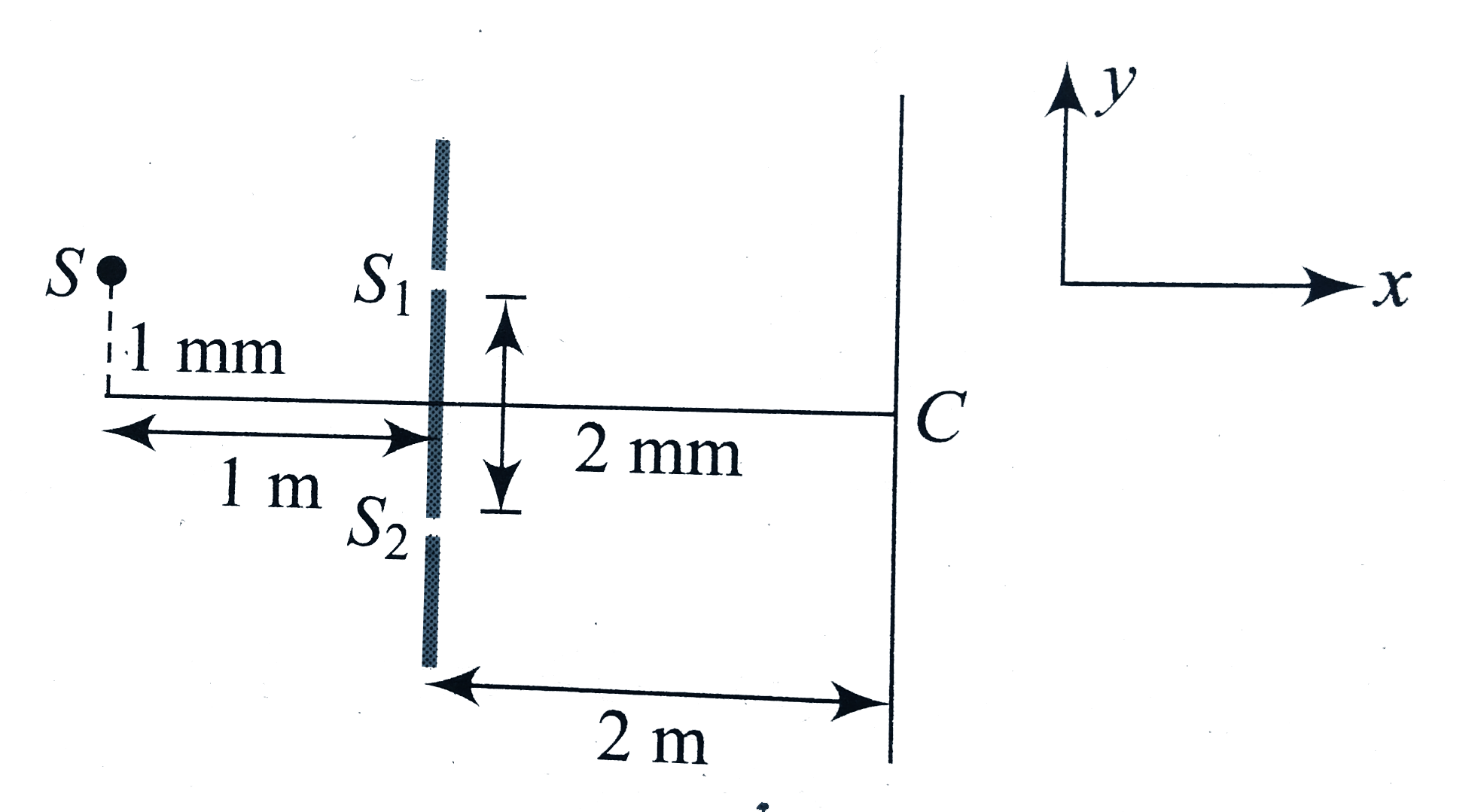
At t=0, fringe width is β1, and at t=2 s, width of figure is β2. ThenAβ1>β2Bβ2>β1Cβ1=β2Ddata is insufficientIn young's double-slit experiment set up, sources S of wavelength 50 nm illumiantes two slits S1 and S2 which act as two coherent sources. The sources S oscillates about its own position according to the equation y=0.5sinπt, where y is in nm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exaclty in front of the upper slit becomes minimum is
 A1 sB2 sC3 sD1.5 s
A1 sB2 sC3 sD1.5 s
Figure shows a Young's double slit experiment set-up. The source S of wavelength 4000Å oscillates along y-axis according to the equation y−sinπt, where y is in millimeters and t is in seconds. The distance two slits S1andS2 is 0.5 mm.

View SolutionIn a Young’s double slit experiment, the source illuminating the slits is changed from blue to violet. The width of the fringes
View SolutionS1andS2 are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is 4Wm−2, the intensity of each source is
View SolutionIn young's double slit experiment, distance between the slit S1andS2 is d and the distance between slit and screen is D . Then longest wavelength that will be missing on the screen in front of S1 is
View SolutionIn the arrangement shown in figure, light of wavelength 6000Å is incident on slits S1 and S2 have been opened such that S3 is the position of first maximum above the central maximum and S4 is the closest position where intensity is same as that of the ligth used, below the central maximum Point O is equidistant from S1 and S2 and O' is equidistant from S3 and S4. Then intensity of inciden light is I0

Find the intensity at O' (on the screen).
View Solution
