In figure, a screen is placed normaol to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.
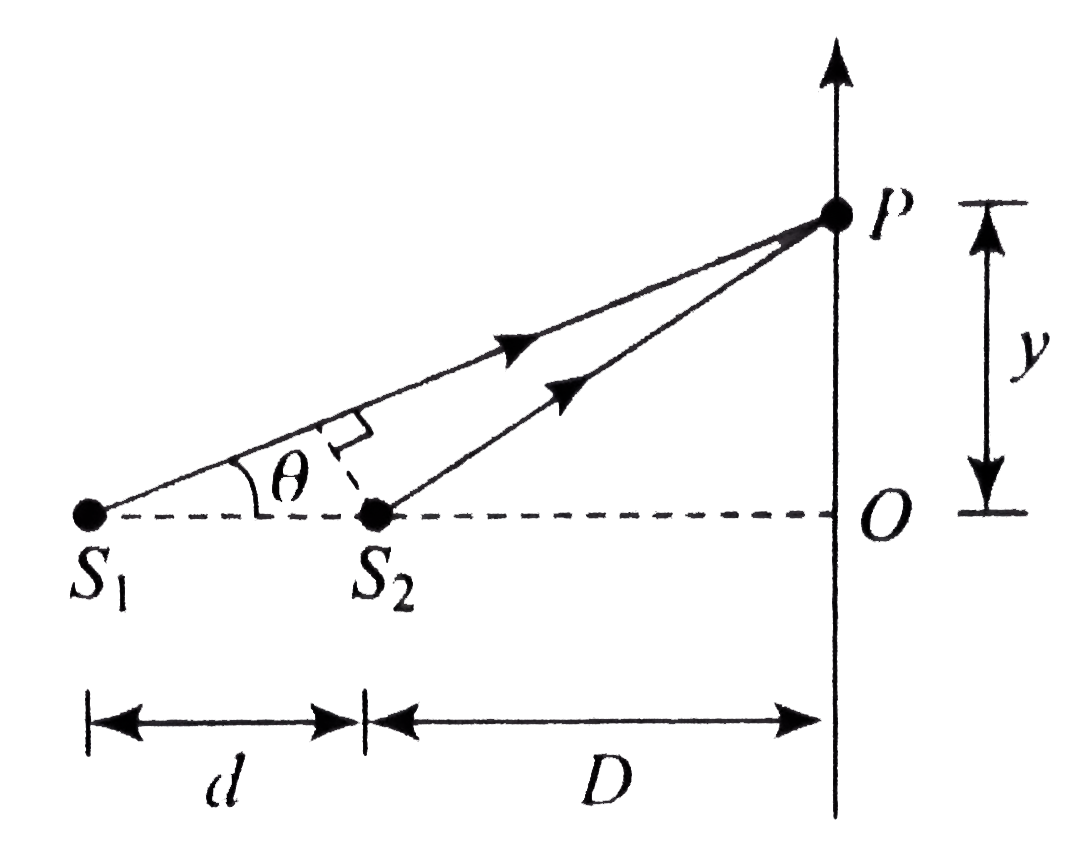
Also, find the value of radius for this ring.
6.32 cm
5.52 cm
4.7 cm
3.25 cm
The correct Answer is:a
The optical path difference at P is
Δx=S1P−S2P=cosθ
∵cosθ=1−θ22 for small θ
∴Δx=d(1−θ22)
=d[1−y22D2], where D+d=D
For nth maxima,
⇒Δx=nλ
d[1−y22D2]=nλ
y = radius of the nth brigth ring
=D√2(1−nλd)
At the central maxima, θ=0
Δx=d=nλ
⇒n=dλ=0.50.5×10−3=1000
Hence, for the closest second brigth ring, n=998.
Putting values, r=6.32cm.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer3videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives4videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK34videos
THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK38videos
WAVES
Similar Questions
In the figure shown, a screen is placed normal to the line joining the two point coherent sources S1andS2. The interference pattern consists of concentric circles.
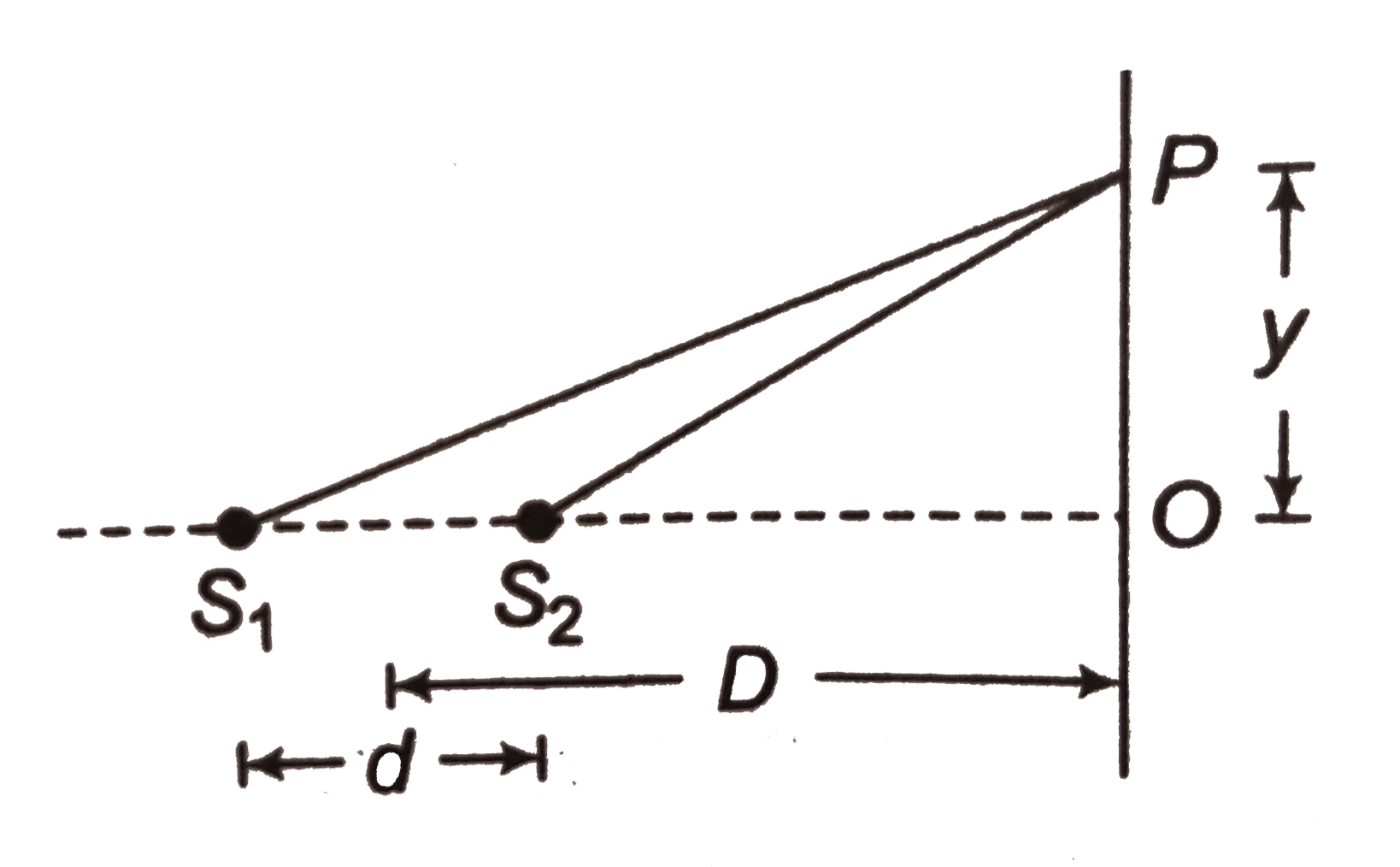
(a)Find the radius of the nth bright ring.
(b) If d=0.5 mm, λ=5000Å and D=100 cm, find the radius of the closest second bright ring.
(c) Also, find the value of n for this ring.View Solutionif the straight line joining the points (3,4) and (2,−1) be parallel to the line joining the points (a,−2) and (4,−a),find the value of a.
View Solution
Knowledge Check
- Question 1 - Select One
In figure, a screen is placed normaol to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.
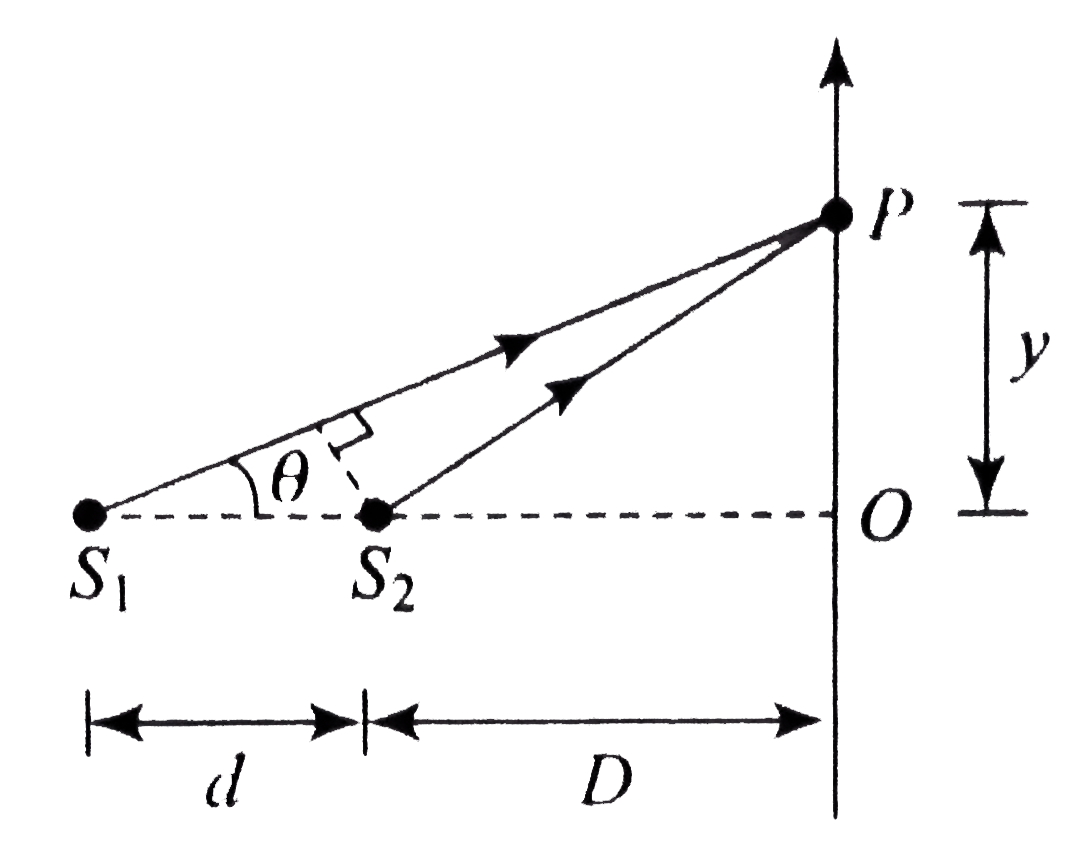
Find the radius of the nth bright ringAD√1(1−nλd)BD√2(1−nλd)C2D√2(1−nλd)DD√2(1−nλ2d) - Question 2 - Select One
In figure, a screen is placed normal to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.
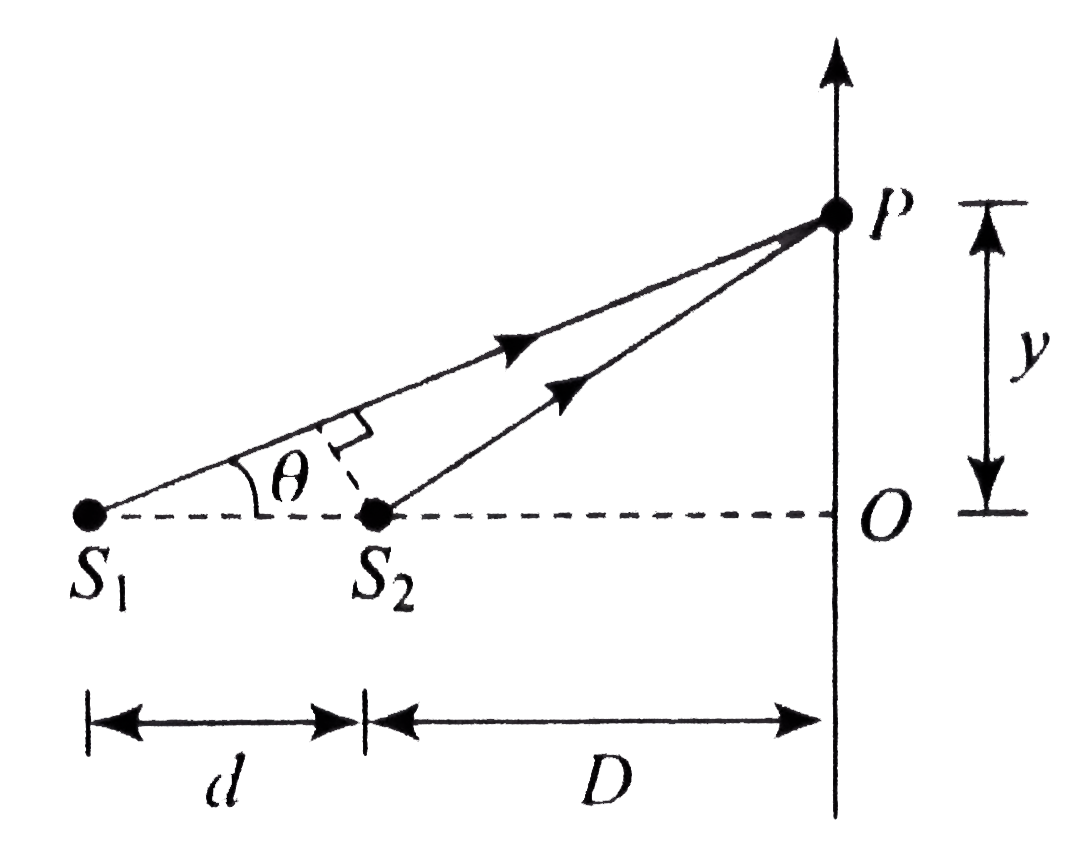
If d=0.5mm,λ=5000Å and D−10cm, find the value of n for the closest second bright ring.A888B830C914D998 - Question 3 - Select One
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
In Young's doulbe-slit experiment the separation between two coherent sources S1 and S2 is d and the distance between the source and screen is D. In the interference pattern, it is found that exactly in front of one slit, there occurs a minimum. Then the possible wavelengths used in the experiment are
View SolutionTwo coherent sources of intensities I1 and I2 produce an interference pattern. The maximum intensity in the interference pattern will be
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 View Solution
View SolutionTwo coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 View Solution
View SolutionIn Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
View Solution

