A uniform constant magnetic field B is directed at an angle of 45∘ to the xaξs in the xy- plane . PQRS is a rigid, square wire frame carrying a steady current I0, with its centre at the origin O. At time t=0, the frame is at rest in the position as shown in figure , with its sides parallel to the xandy axis. Each side of the frame is of mass M and length L.
(a) What is the torque τ about O acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time Δt, and the axis about this rotation occurs .(Δtissoshorttˆanyvariation∈the→rquedur∈gthis∫ervalmaybe¬≤cted.)Given:themomentof∫eriaoftheameaboutanaξsthroughitscentreperpendica––r→itsaboutanaξsthroughitscentreperpendica––r→itspla≠is(4)/(3) ML^(2).
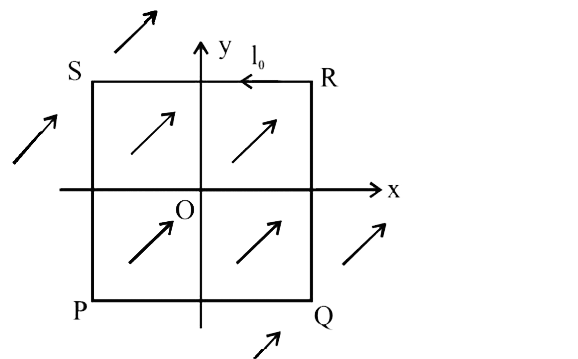
(a) As magnetic field is in x-y plane and subtended an angle of
45∘ with x-axis,
Bx=Bcos45∘=B/√2
and BY=Bsin45∘=B/√2
so, in vector form →B=ˆi(B/√2)+ˆj(B/√2)
and →M=I0Sˆk=I0L2ˆk
⇒→τ=→M×→B=I0L2ˆk×(B√2ˆi+B√2ˆj)
⇒→τ=I0L2B√2×(−ˆi+ˆj)
i.e,torque has magnitude I0L2B and
is directed along the line QS from
Q to S.

(b) By the theoram of perpendicular
axis, moment of inertia of the frame
about QS,
IQS=12Iz=12(43ML2)=23ML2
as τ=Iα⇒ατI=I0L2B×32L2M=32I0BM
As here α is constant, equation of circular motion are
valid. Hence, from θ=ω0t+12αt2, with ω0=0, we have
θ=12αt2=12(32I0BM)(Δt)2=34I0BMΔt2
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
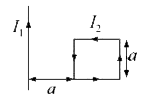
A rigid square loop of side 'a’ and carrying current I2 is lying on a horizontal surface near a long current I1 carrying wire in the same plane as shown in figure. The net force on the loop due to the wire will be:
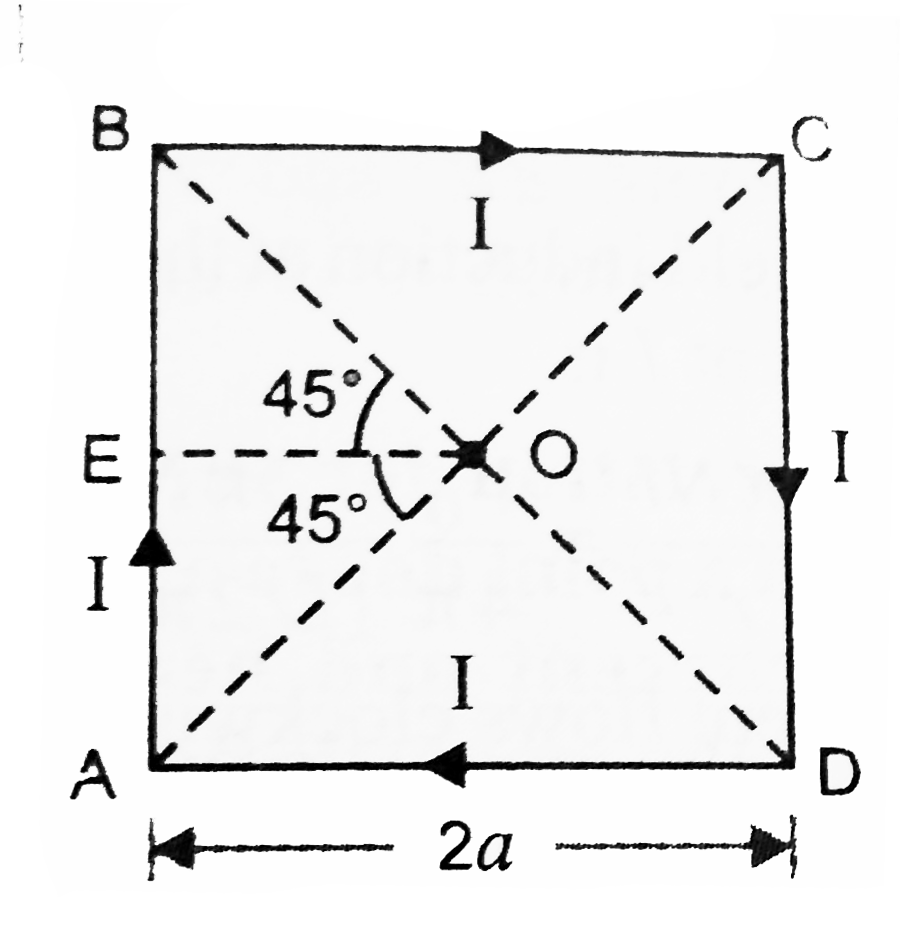
View SolutionFind the experssion for the magnetic field at the centre O of a coil bent in the form of a square of side 2a, carrying current I, figure.
View Solution
Knowledge Check
Current flows through uniform, square frames as shown in the figure. In which case is the magnetic field at the centre of the frame not zero?
A B
B C
C D
D
Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
A B
B C
C D
D
Four identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
Athe x-axis is (2/3)ml2Bthe z-axi is (43)ml2Can axis parallel to the z-axis and passing through a corner is (10/3)ml2Done side is (5/2)ml2
A rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
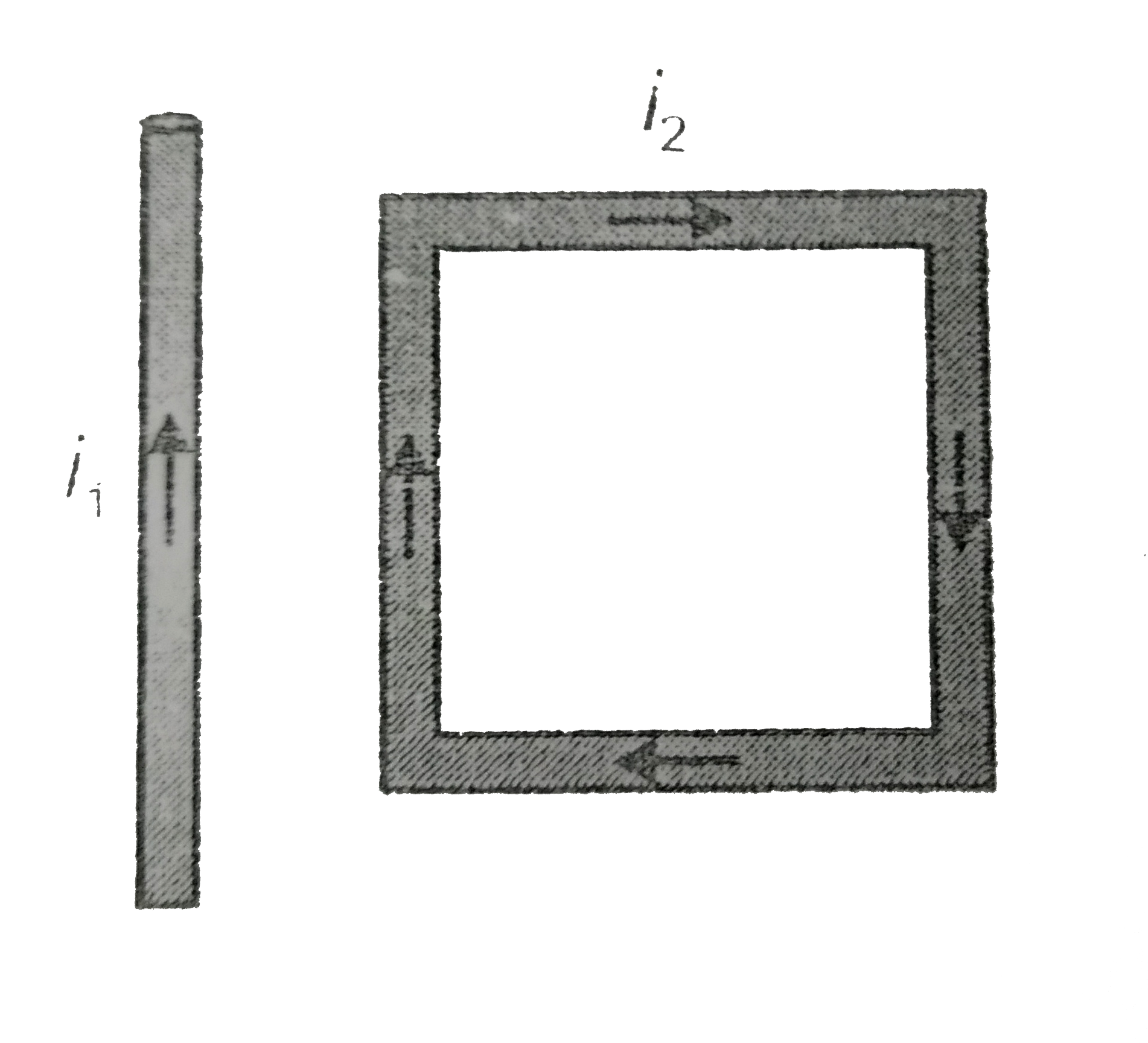
View SolutionA square frame carrying a current I is located in the same plane as a long straight wire carrying a current I0 The frame side has a length a. The axis of the frame passing through the midpoints of the opposite sides is parallel to the wire and is separated from it by the distance which is η times greater than the side of the frame. Find
(a) Force acting on the frame
(b) The mechanical work to be performed in order to turn the frame through 180∘ about its axis, with the currents maintained constant.
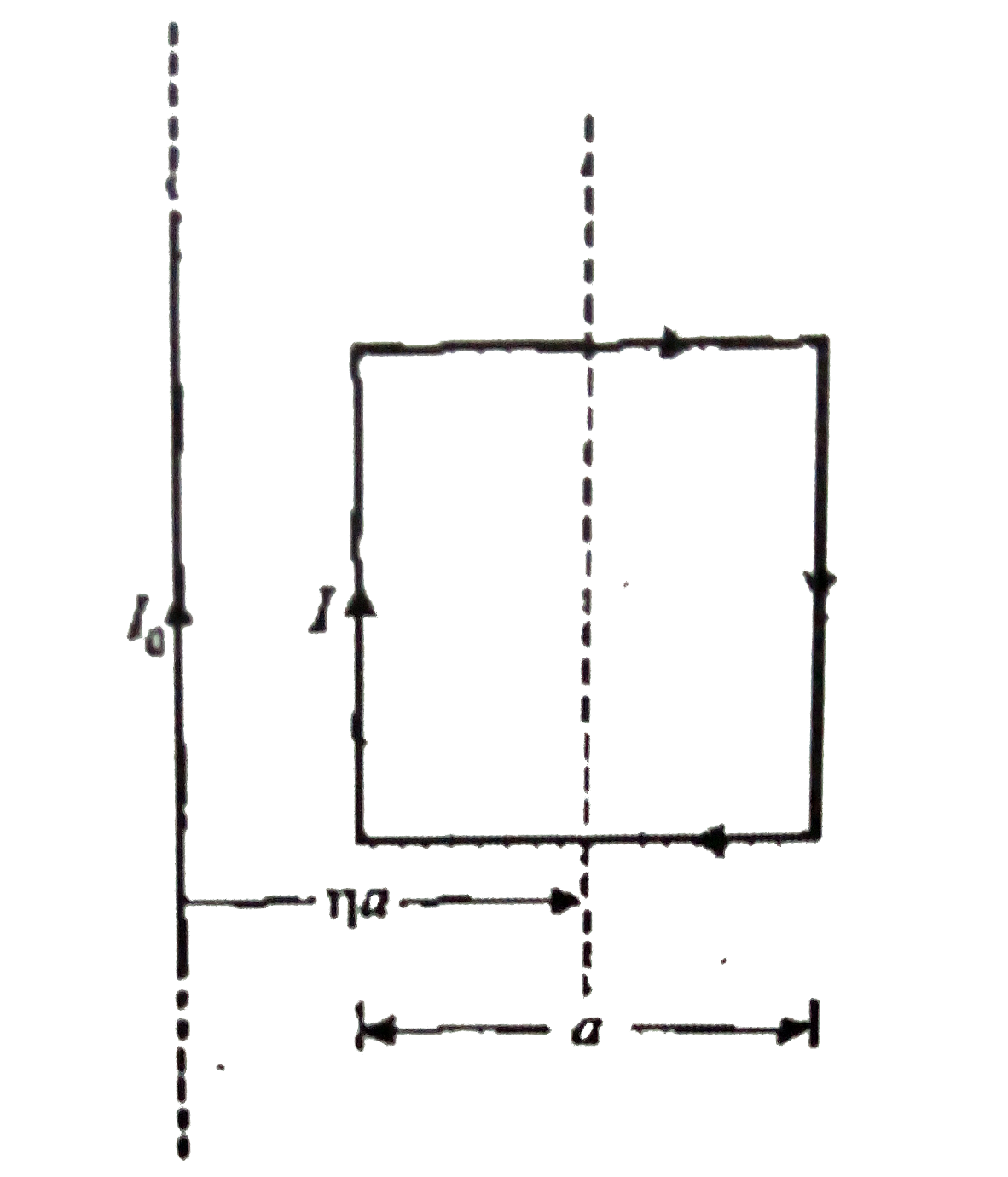
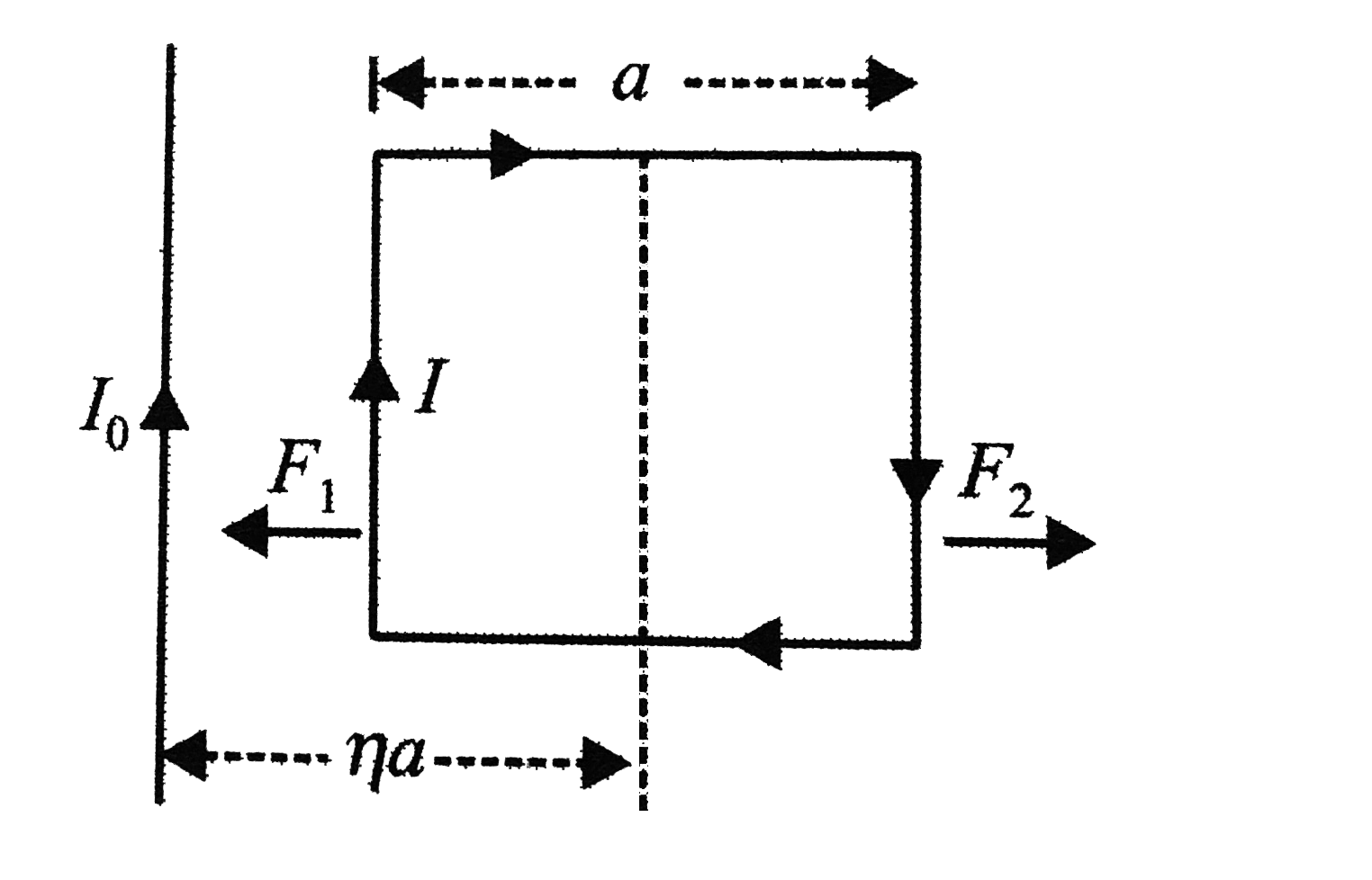
View SolutionA square frame carrying a current I=0.90A is located in the same plane as a long straight wire carrying a current I0=5A, The frame side has a length a=8cm. The axis of the frame passing through the mid-point of the opposite sides is parrallel to the wire and is separated form it by a distance h=15 times greater tahn the side of the frame.
Find:
(a) ampere force acting on the frame.
(b) The machanical work to be performed in order to turn the frmae through 180∘ about its axis, with the current maintained constant.
View SolutionFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
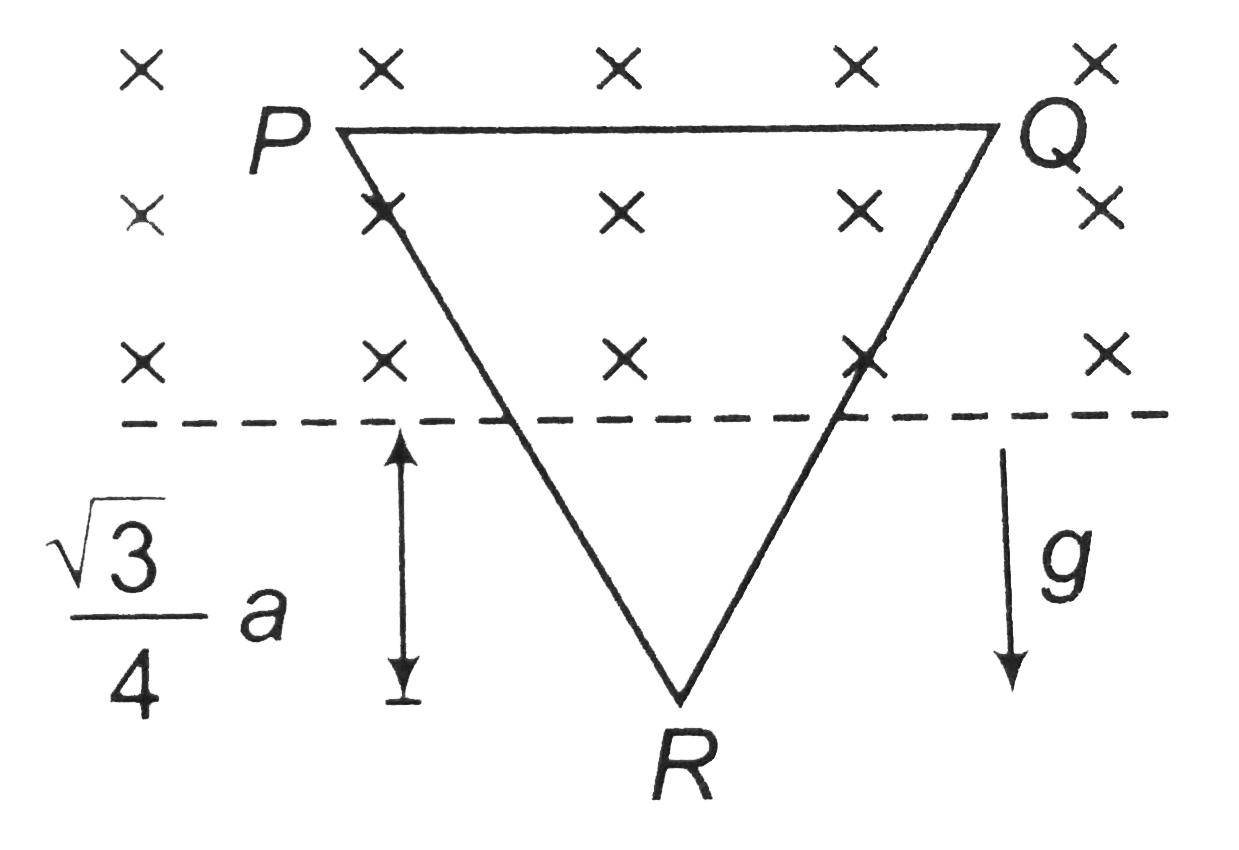
View SolutionAn equilateral triangle frame PQR of mass M and side a is kept under the influence of magnetic force due to inward perpendicular magnetic field B and gravitational field as shown in the figure. The magnitude and direction of current in the frame so that the frame remains at rest is
View Solution
