A positively charged particle having charge q1=1C and mass m1=40gm is revolving along a circle of radius R=40cm with velocity v1=5ms−1 in a uniform magnetic field with center of circle at origin O of a three-dimensional system. At t=0, the particle was at (0, 0.4m, 0) and velocity was directed along positive x direction. Another particle having charge q2=1C and mass m2=10g moving uniformly parallel to positive z-direction with velocity v2=40/πms−1 collides with revolving particle at t=0 and gets stuck to it. Neglecting gravitational force and coulomb force, calculate x-, y- and z-coordinates of the combined particle at t=π/40s.
In three dimensional co-ordinate system, axes are assumed according to right hand screw rule.
Consider such a system shown in Fig. In this system positive z direction is normal to plane of paper and is directed towards the reader.
The particle is positively charged, centre of its circular path is at origin and when the particle is on positive y-axis , its velocity is directed along positive x-direction, it means that the particle is moving clockwise

Since the particle is positively charged, therefore, current associated with its motion is also clockwise or along positive x direction at (0,0.4,0).
Lorentz's force is toward origin. Therefore, according to Fleming's left hand rule, magnetic induction B must be along positive z-direction.
Radius of circular path followed by this particle is r1=0.4m
But r1=m1v1q1B⇒B=m1v1q1r10.5T
Now the second particle collides and gets struck with it. Velocity of combined particle can be found out by applying law of conservation of momentum.
(m1+m2)→v=m1→v1+m2→v2
(40×10−3+10×10−3)→v
=(40×10−3)×5ˆi+(10×10−3)40πˆk
∴ x-direction of velocity of combined particle is vx=4ms−1
and z-direction, vz=8πms−1
Due to vx, combined particle tries to move clockwise along a circular path and due to vzit ties to move uniformly along z-axis.
Therefore, its ultimate path becomes helix. Radius of this helix is
R=(m1+m2)vx(q1+q2)B=0.2m
and period of revolution T=2π(m1+m2)(q1+q2)B=π10s
The particle turns by angle π/2 in time π/4s.
∴ x-coordinate of new position of combined particle =R=0.2m
→ y-coordinate=r1−R=0.2m
and z-direction =vzt=0.2m
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.122videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.213videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank31videos
KINETIC THEORY
- BOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank50videos
Magnetism and Matter
Similar Questions
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
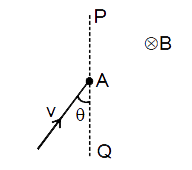
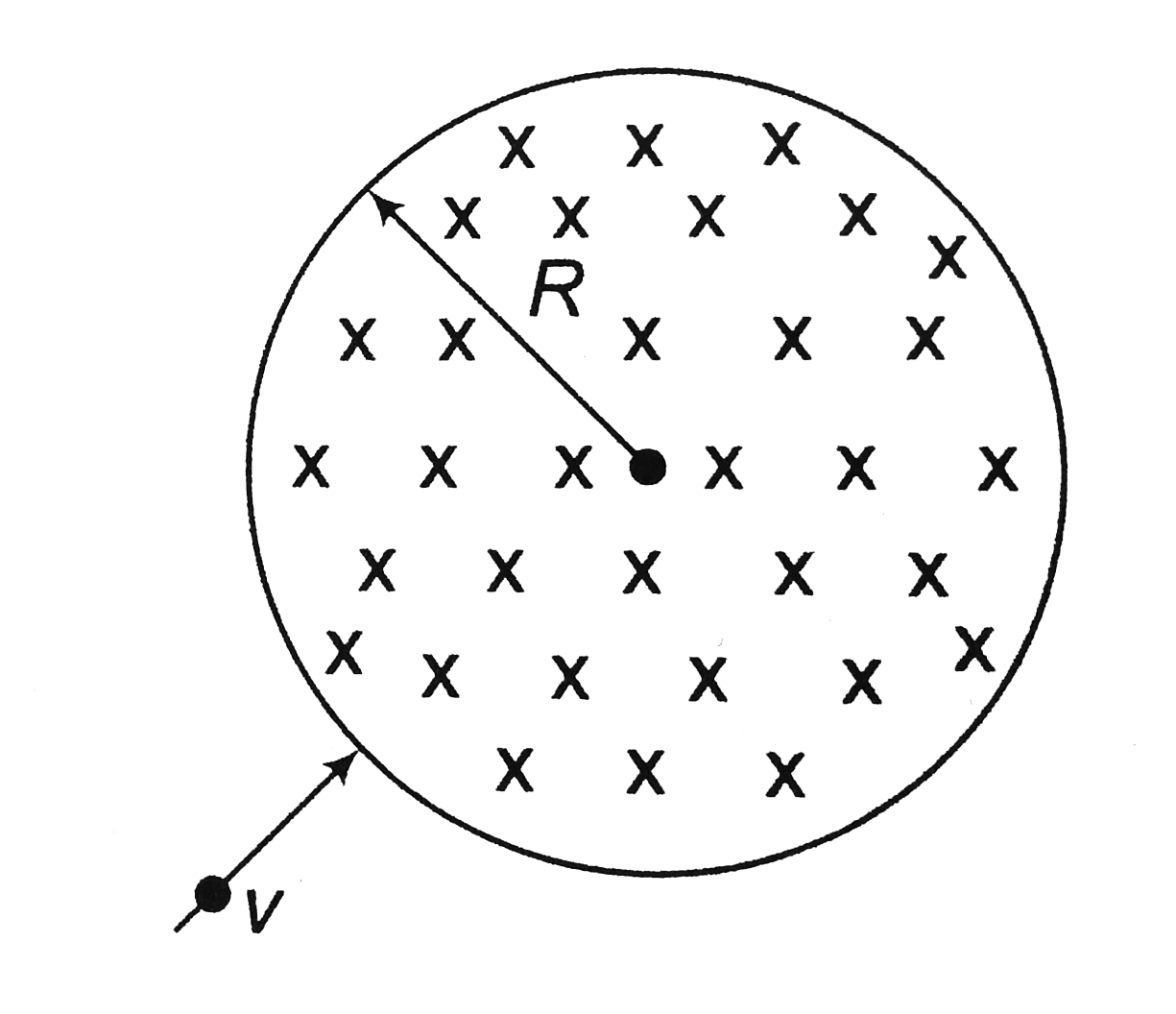
impulse of magnetic force.View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A charge particle (charge q ) is moving in a circle of radius R with uniform speed. v The associated magnetic moment m is given by
AqvR2BqvR2/2CqvRDqvR/2 - Question 2 - Select One
A particle having a charge of 10.0μC and mass 1μg moves in a circle of radius 10 cm under the influence of a magnetic field of induction 0.1T. When the particle is at a point P, a uniform electric field is switched on so that the particle starts moving along the tangent with a uniform velocity. The electric field is
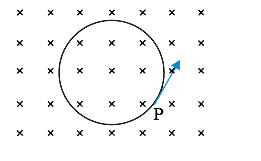 A0.1V/mB1.0V/mC10.0V/mD100V/m
A0.1V/mB1.0V/mC10.0V/mD100V/m - Question 3 - Select One
A particle having charge of 20μC and mass 20μg moves along as circle of radius 5cm under the action of a magnetif field B=0.1 tesla. When the particle is at P, uniform transverse electric field is switched on an it is found that the particle continues along the tangent with a uniform velocity. Find the electric field
 A2VmB0.5VmC5VmD1.5Vm
A2VmB0.5VmC5VmD1.5Vm
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic fieldView SolutionA particle having a charge20μC and mass 20μg moves along a circle of radius 5.0 cm under the action of a magnetic field 5.0 cm under the action of a magnetic field B = 1.0 T. When the particle is at a point P, a uniform electric field is switched on and it is found that the particla continues on the tangent through P qith a uniform velocity. Find the electric field.
View SolutionA charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
View SolutionTwo charged particles having charge 1μC and −μC and of mass 50gm each are held ar rest while their separtion is 2m. Find the relative velocity of the particles when their separation is 0.5m.
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).
 View Solution
View Solution

