In an LC circuit as shows in Fig. the switch is closed at t=0.Qmax=100μC, L=40mH, C=100μF.
a. Determine the equation for instantaneous change on the capacitor.
b. Determine the equation for instantaneous current in the circuit.

a. q=Qmaxcosωt, Here Qmax=100μC,
ω=1√LC=1√(40×10−3)(100×10−6)=500rads−1
q=100cos(500t)μC
b. i=−dqdt=(100)(500)sin(500t)μA
or i=50000sin(500t)μA
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Determine the charge on the capacitor in the following circuit in μC ________.

View SolutionThe circuit shows in Fig. is in the steady state with switch S1 closed. At t=0,S1 is opened and switch S2 is closed.
a. Derive expression for the charge on capacitor C2 as a function of time.
b. Determine the first instant t, when the energy in the inductor becomes one-third of that in the capacitor.

View Solution
Knowledge Check
In the circuit shown in figure, the switch S is closed at t=0. If VL is the voltge induced across the inductor and i is the instantaneous current, the correct variation of VL versus is given by
 A
A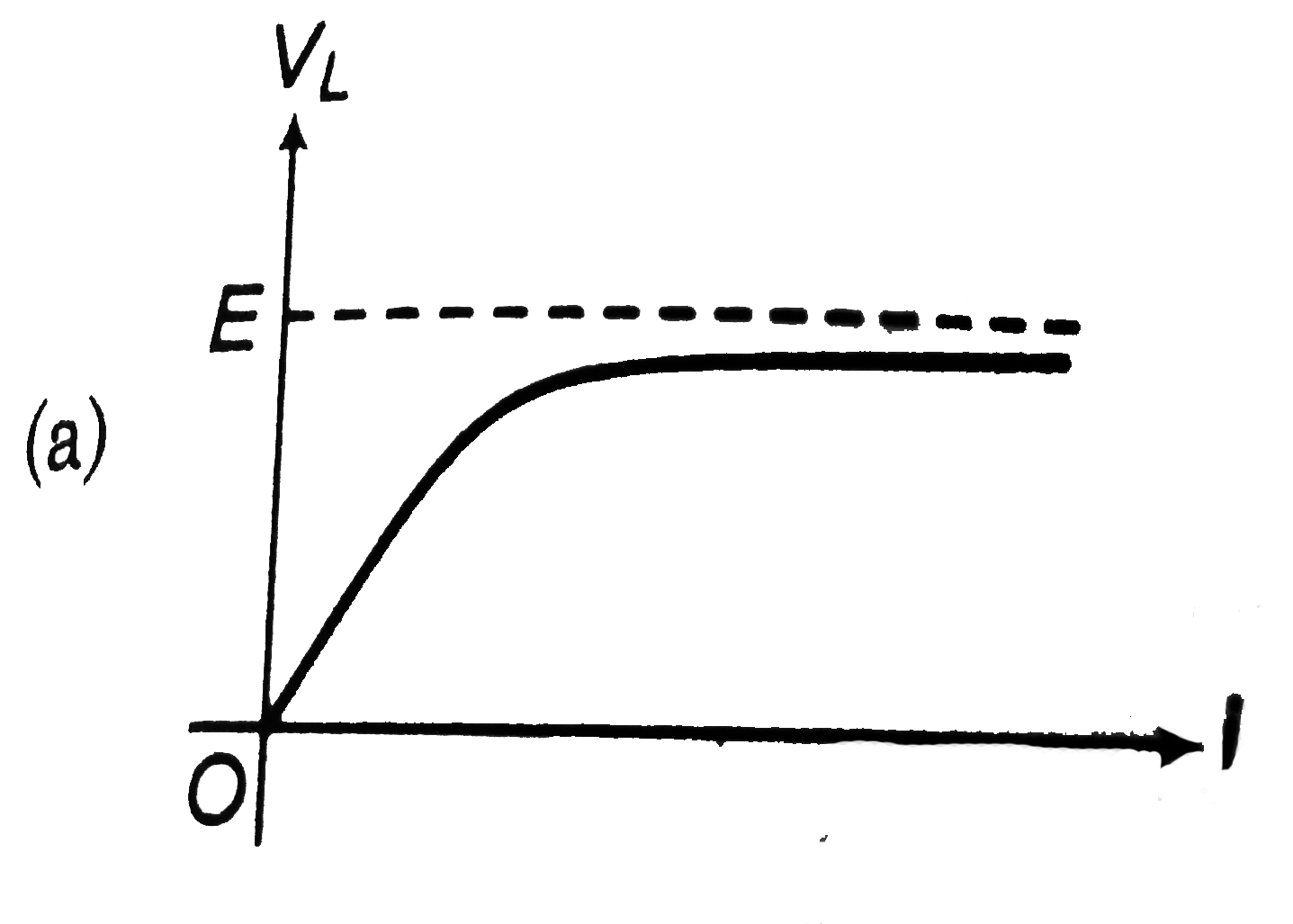 B
B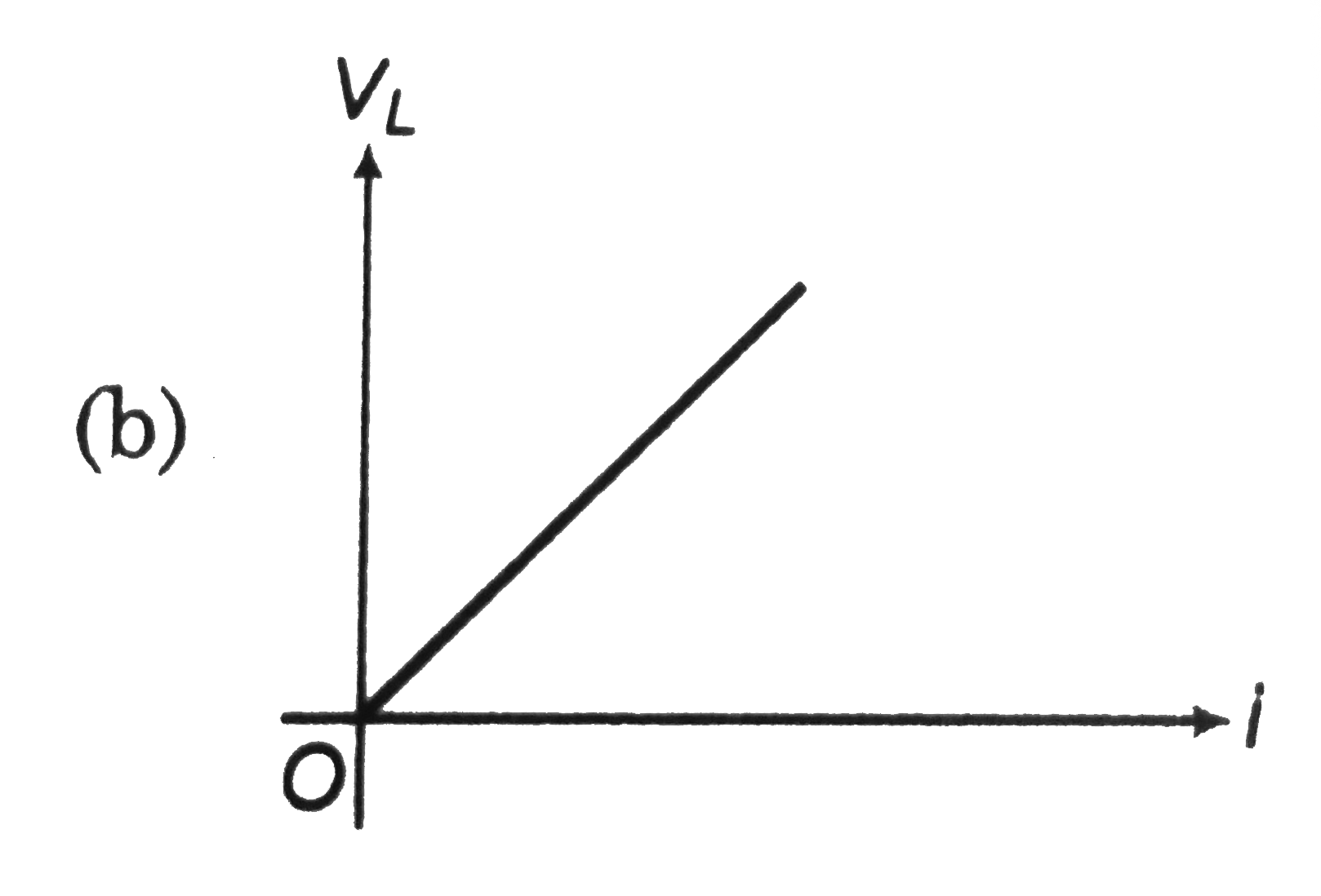 C
C D
D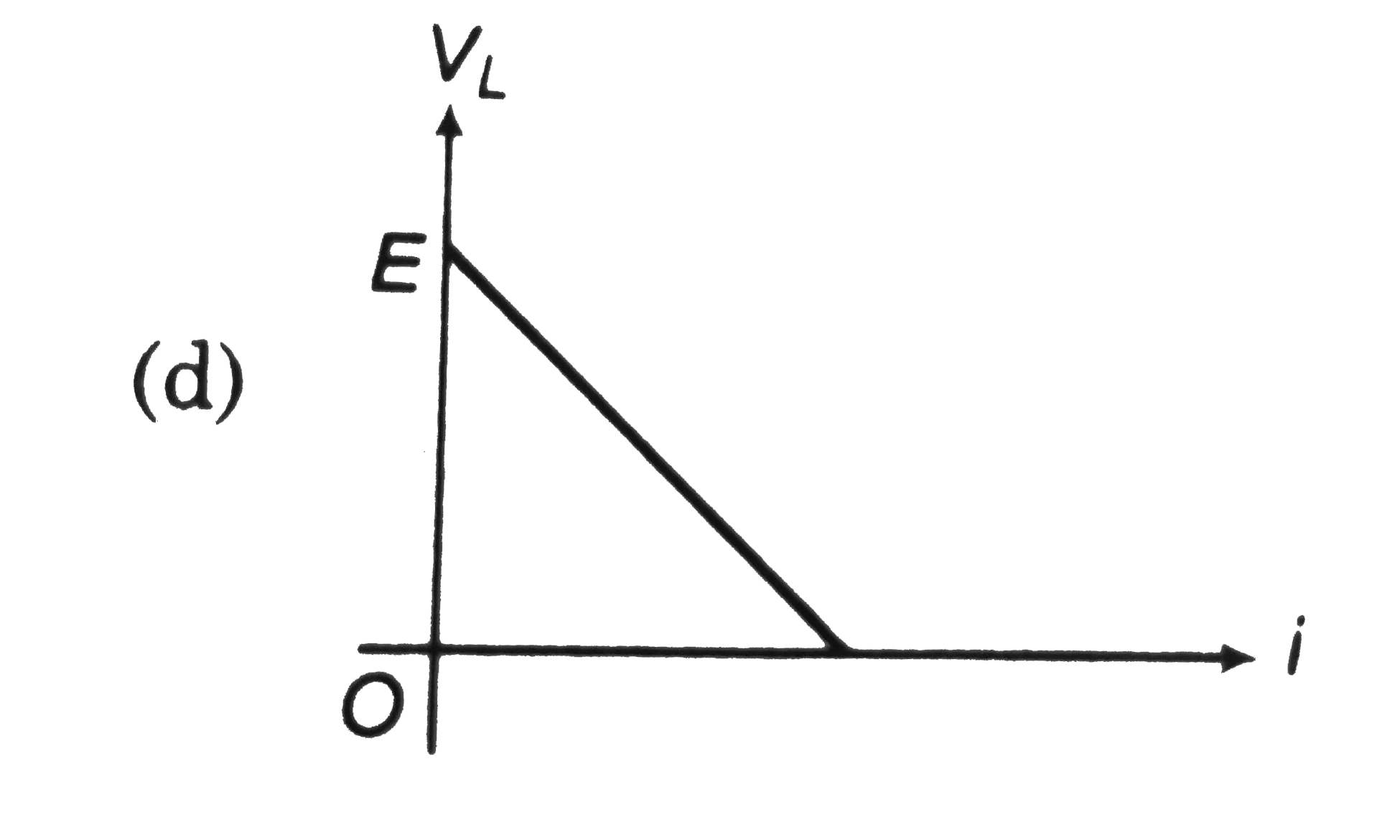
In an AC circuit , an alternating voltage e = 200sin 100t V is connected to a capacitor of capacity 1μF . The rms value of the current in the circuit is
A100 mAB200 mAC20 mAD10 mAIn the circuit shown if Fig. the switch S is closed at time t = 0. The current through the capacitor and inductor will be equal at time t equal (given R=√L/C
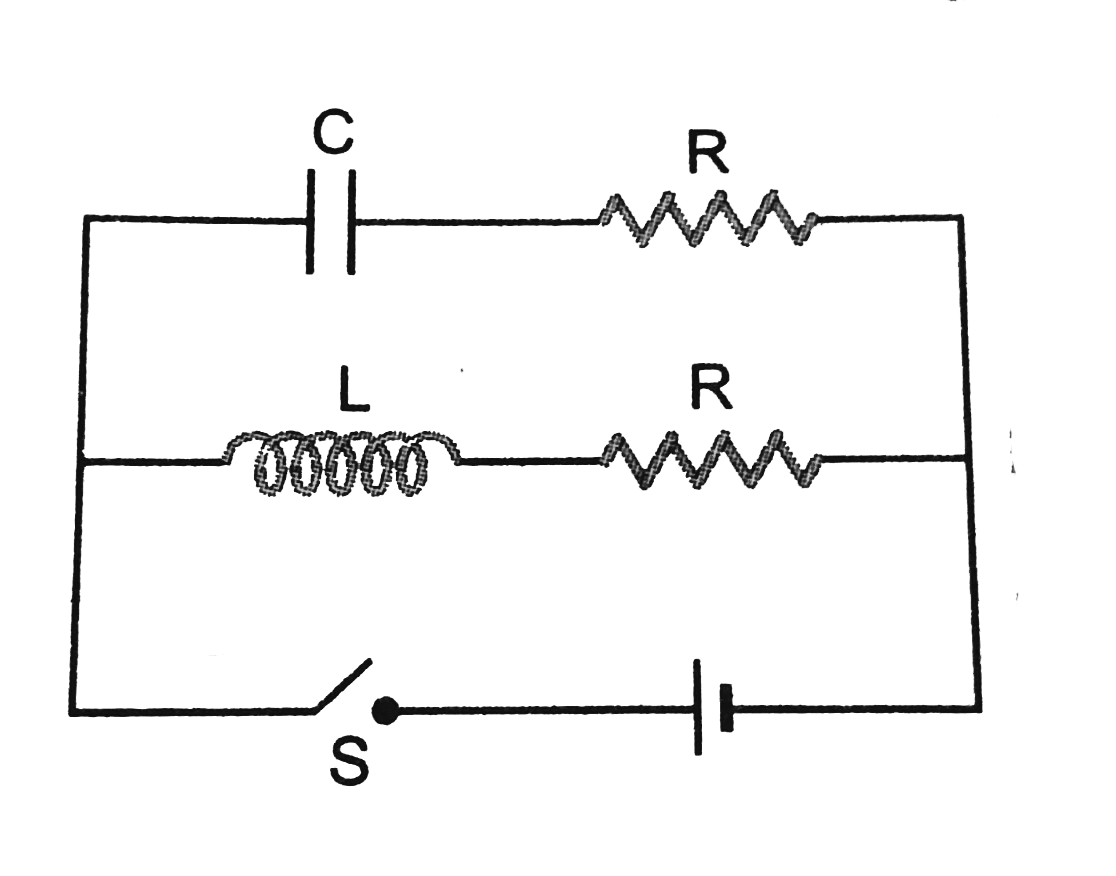 ARCBRCloge2C1RlogeDLR
ARCBRCloge2C1RlogeDLR
A 60μF capacitor is connected to a 110 V, 60 Hz a.c. supply Determine the r.m.s value of current in the circuit.
View SolutionA capactior of 1μF is connected ot an a.c. source of e.m.f E=250sin100πt. Write an equation for instantaneous current through the circuit and given reading of a.c. ammeter connected in the circuit.
View SolutionAn LC circuit oscillating at natural frequency conssts of an inductor of inductance 30 m H and a capacitor of capacitance 60μF. The maximum value of instantaneous charge on capacitor in the circuit is 200 μC . If I is the current in the circuit then answer the following :
(i) What is the value of dIdt when charge is 150 μC?
(ii) Calculate the value of I when charge is 200 μC .
(iii) Find the maximum value of I.
(iv) For what value of q I is half of its maximum value ?
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
View SolutionIn the circuit shown below the switch is closed at t=0. For 0<t<R(C1+C2), the current I1 in the capacitor C1 in terms of total current I is

View Solution
