If the current in the inner loop changes according to I=2t2 (Fig .), then find the current in the capacitor as a function of time.

M=μ02bπa2
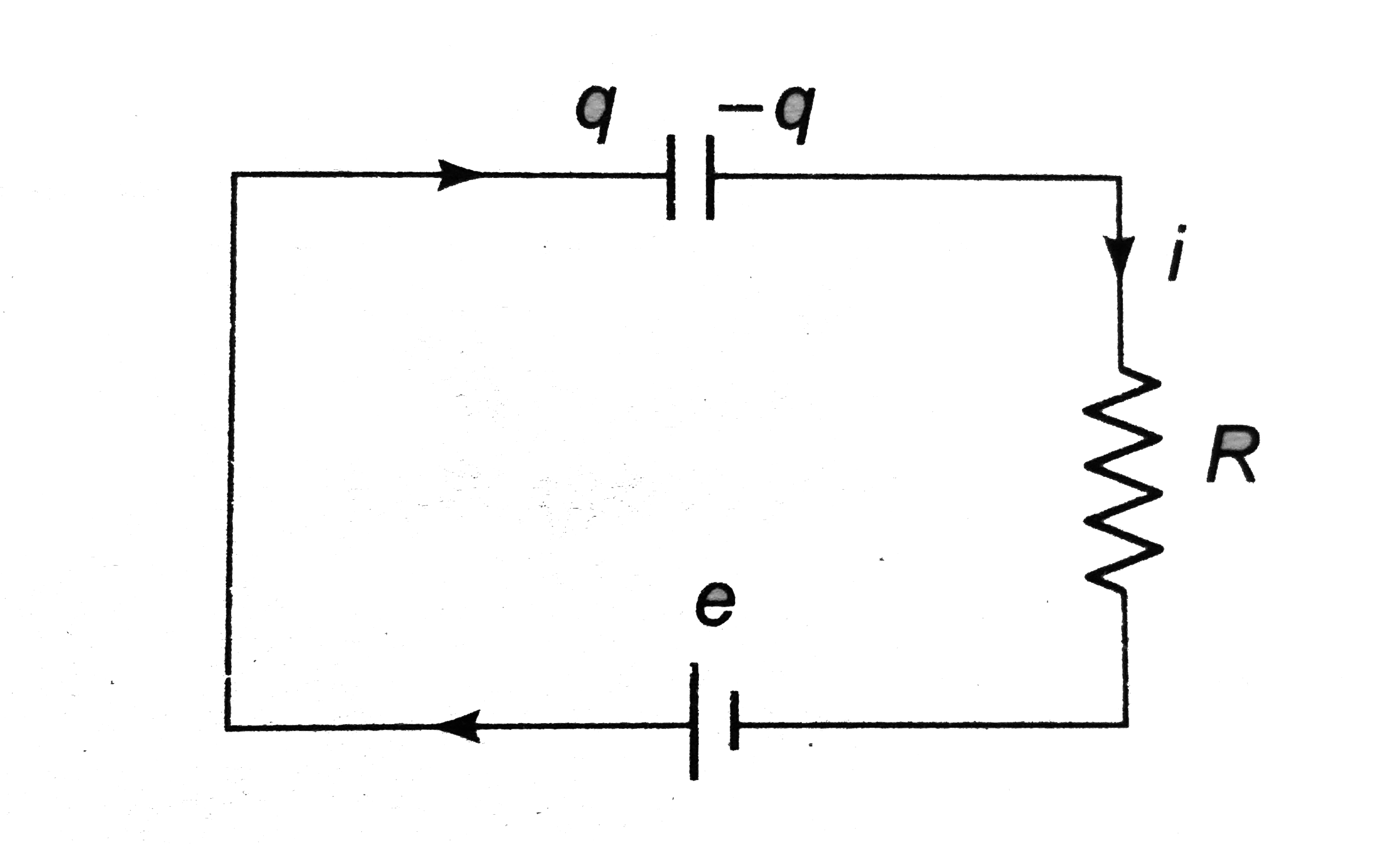
|emf induced in larger coil|=[(didt) in smaller coil]
e=μ02bπa2(4t)=2μ0πa2tb
Applying KVL,
+e−qC−iR=0⇒2μ0πa2tb−qC−iR=0
Differentiating w.r.t. time, we get
2μ0πa2b−iC−didtR=0=0
On solving, i=2μ0πa2Cb[1−e−t/RC]
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
If the current in the inner loop changes according to i=2t2 then, find the current in the capacitor as a function of time.

View SolutionIf the current in the ineer loop changes according to i=2t2 then, find the current in the capacitor as a function of time.

View SolutionFigure. shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop, if a capacitor of capacitance C is also connected in the larger loop as shows in Fig . , find the charge on the capacitor as a function of time.

View SolutionIf a capacitor of capacitance C is also connected in the larger loop as shows in Fig . , find the charge on the capactior as a function of time.

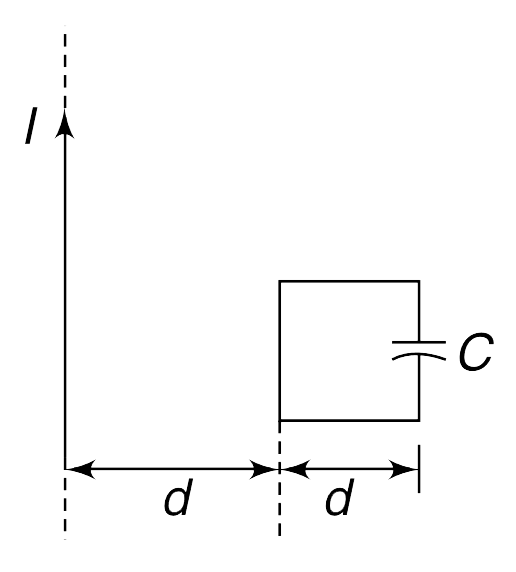
View SolutionA square loop of side length d has a capacitor of capacitance C and the resistance of the loop is R. In the plane of the loop there is a long straight current carrying wire having current I. The distance of the straight wire from the loop is d as shown in figure. The current in the straight wire is made to grow with time as I=αt where α=2As−1. Neglect self inductance of the loop.
(a) Find the charge on the capacitor as a function of time (t).
(b) Find the heat generated in the loop as a function of time.
(c) Who supplies energy for heat dissipation?
View SolutionIn Fig. 30-44, after switch S is closed at time t = 0, the emf of the source is automatically adjusted to maintain a constant current i through S. (a) Find the current through the inductor as a function of time. (b) At what time is the current through the resistor equal to the current through the inductor?

View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
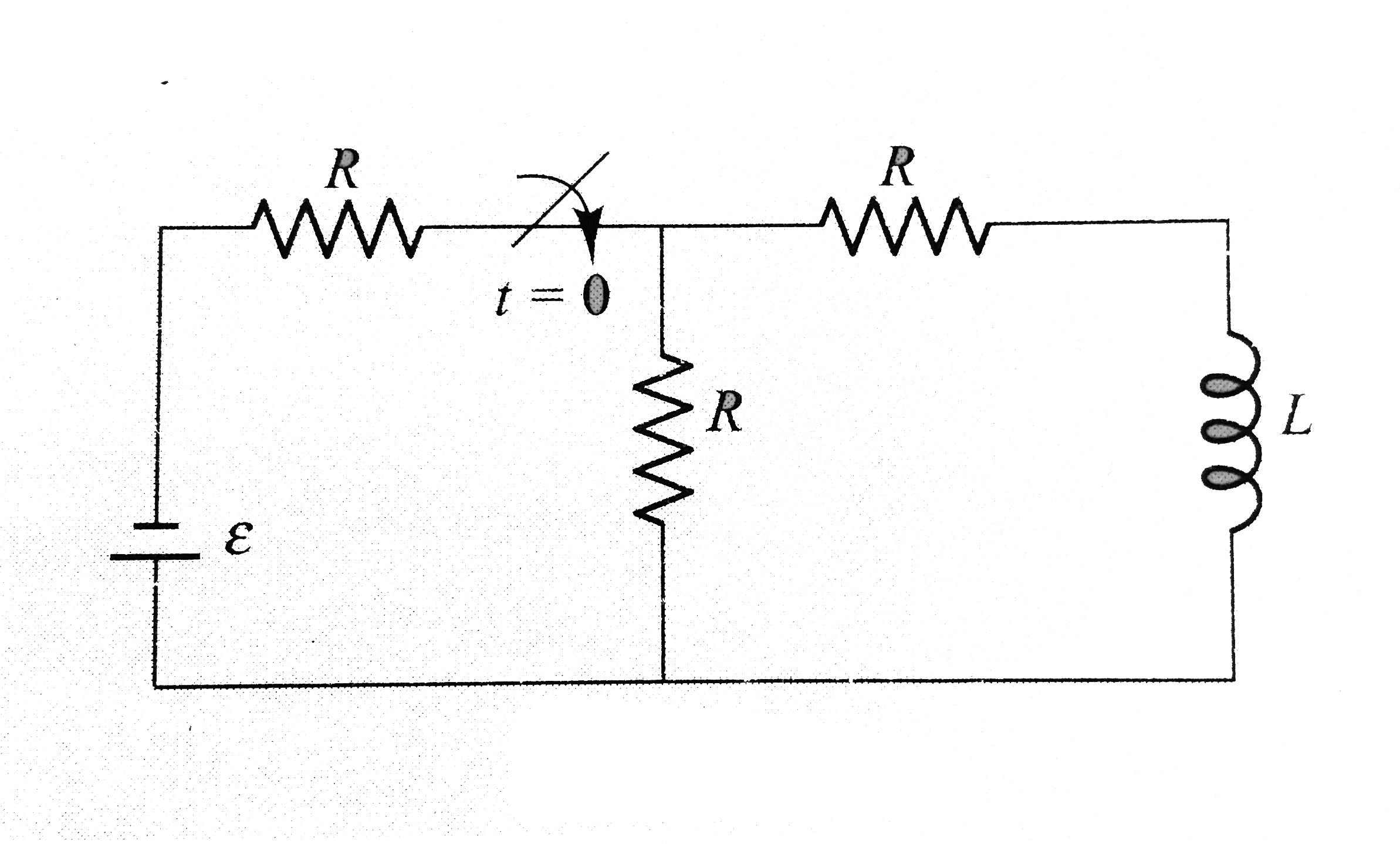
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
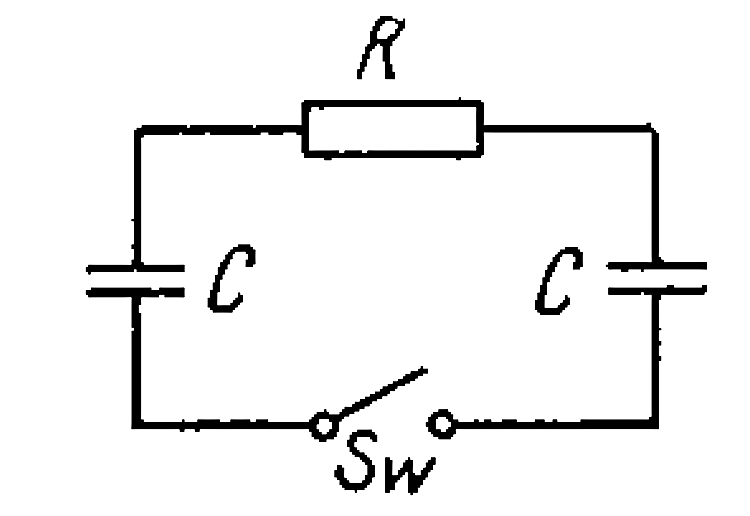
View SolutionIn a circuit shown in fig. the capacitance of each capacitor is equal to C and the resistance, to R One of the capacitor was connected to a voltage V0 and then at the moment t=0 was shorted by means of the swich Sw. Find:
(a) a current I in the circuit as a function of time t:
(b) the amount of generated heat provided a dependence I(t) is known.
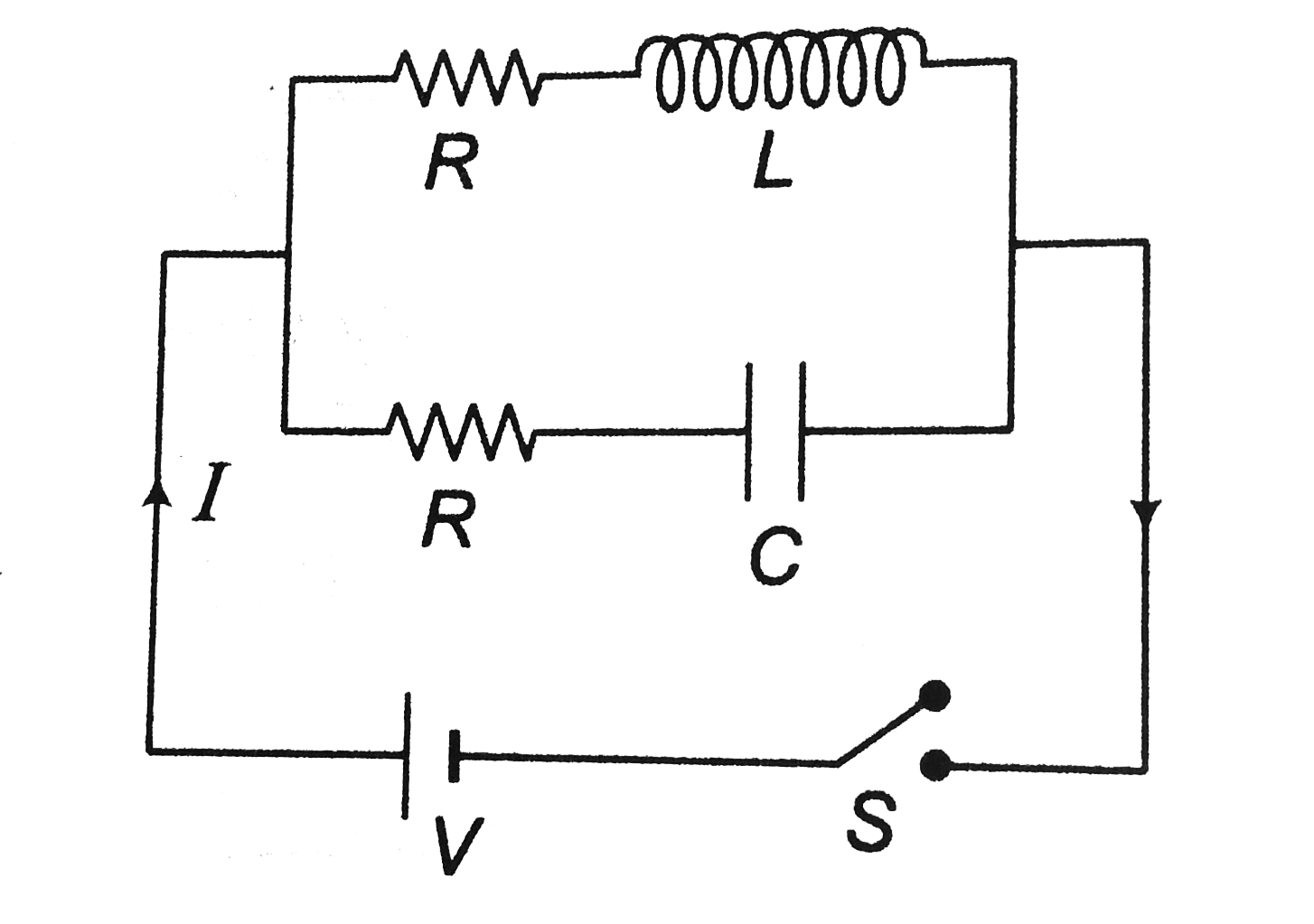
View SolutionIn the circuit diagram shown, initially there is no energy in the inductor and the capacitor, The switch is closed at t=0. Find the current I as a function of time if R=√L/C
View Solution
