If the current in the ineer loop changes according to i=2t2 then, find the current in the capacitor as a function of time.

M=μ02bπa2
|emf induced in larger coil |=m[(didt) in smaller coil]⇒e=μ02bπa2(4t)=2μ0πa2tb
Applying KVL:-
+e−qc−iR=0
2μ0πa2tb−qc−iR=0
differentiate wrt time:-
2μ0πa2b−ic−didtR=0
so solving it
i=2μ0πa2Cb[1−e−t/RC]
Similar Questions
If the current in the inner loop changes according to I=2t2 (Fig .), then find the current in the capacitor as a function of time.
 View Solution
View SolutionFind the current in the loop
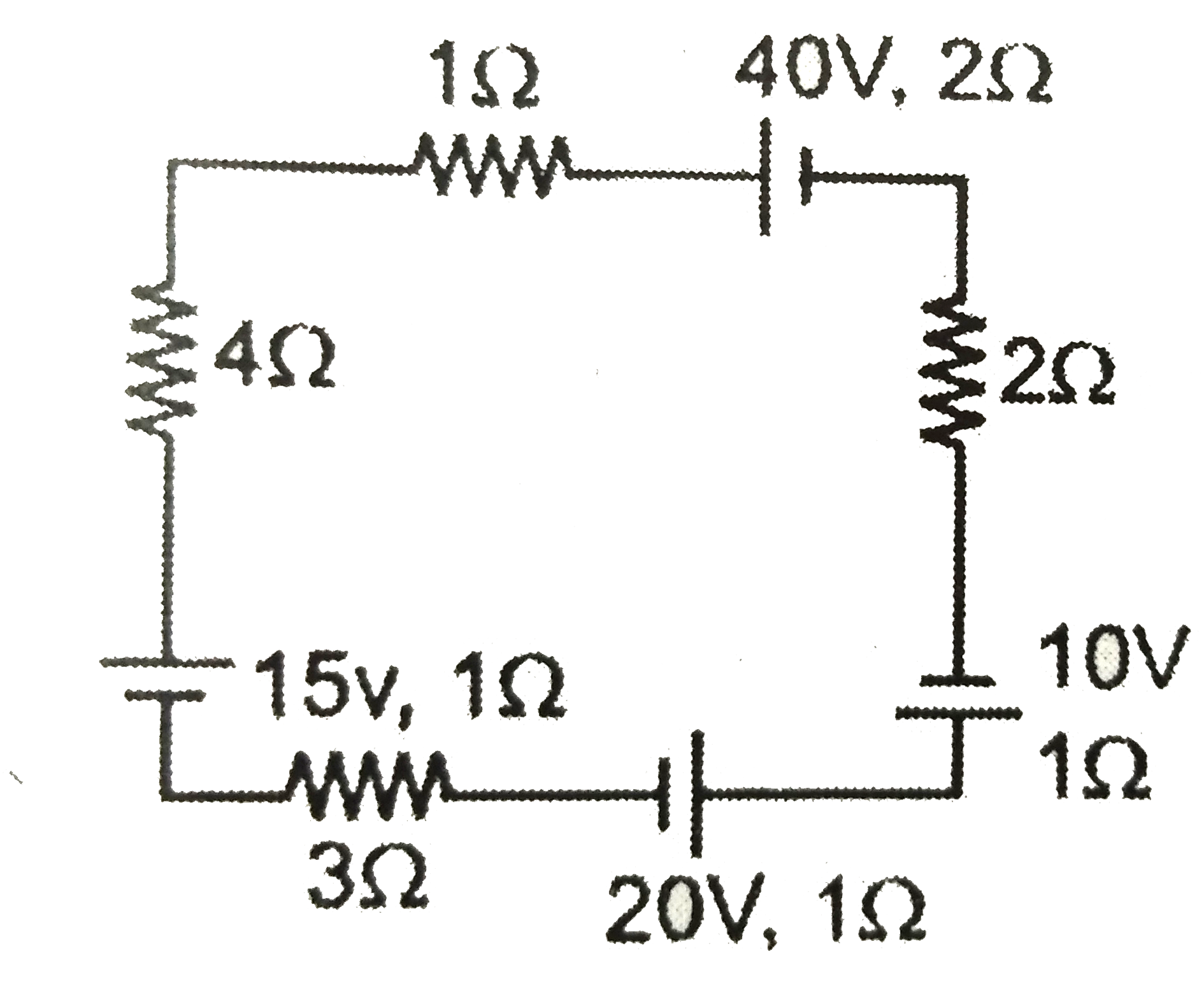 View Solution
View SolutionFind the current in the loop.
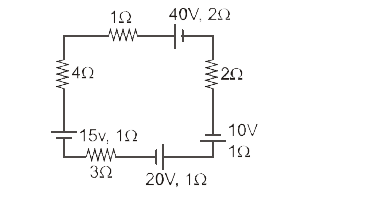 View Solution
View SolutionFind the current in the loop.
 View Solution
View SolutionIf q=2t2+3, find current at t=2 sec ?
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
 View Solution
View SolutionFigure. shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop,
a. find the mutual inductance of the two coils,
b. find the emf induced in the larger coil,
c. if the resistance of the larger loop is R, find the current in it as a function of time.
 View Solution
View SolutionFigure shows tow concentric coplanar coils with radii a and b (a<<b). A current i=2t flows in the smaller loop. Neglecting self inductance of larger loop

(a) Find the mutual inductance of two coils.
(b) Find the emf induced in the larger coil
(c) If the resistance of the larger loop is R find the current in it as a function of time.View SolutionA square loop of side length d has a capacitor of capacitance C and the resistance of the loop is R. In the plane of the loop there is a long straight current carrying wire having current I. The distance of the straight wire from the loop is d as shown in figure. The current in the straight wire is made to grow with time as I=αt where α=2As−1. Neglect self inductance of the loop.
(a) Find the charge on the capacitor as a function of time (t).
(b) Find the heat generated in the loop as a function of time.
(c) Who supplies energy for heat dissipation?
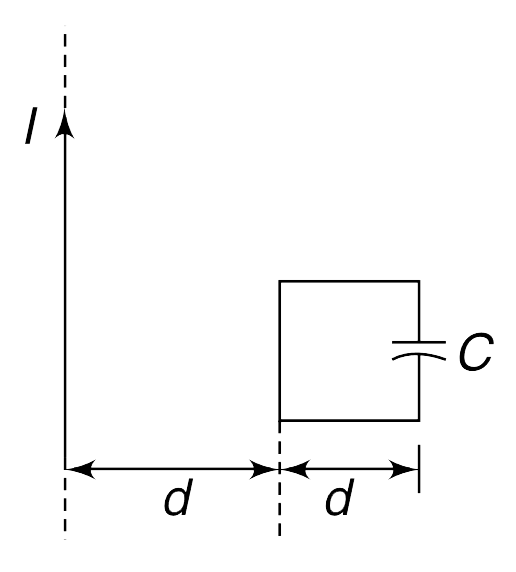 View Solution
View SolutionIn Fig. 30-44, after switch S is closed at time t = 0, the emf of the source is automatically adjusted to maintain a constant current i through S. (a) Find the current through the inductor as a function of time. (b) At what time is the current through the resistor equal to the current through the inductor?
 View Solution
View Solution

