An external magnetic field is decreased to zero, due to which a current is induced in a circular wire loop of radius r and resistance R placed in the field. This current will not become zero at the instant when B stops changing

A

At the instant when external magnetic field stops changing (t=0), the current in the loop is i0. The current in the loop as a function of time for t>0 is given by i0e−2Rt/μ0π.

B

For the same as in option (a), the current in the loop as a function of time t=0 is given by μ0iR2r.

C

The time in which current in loop decreases to 10−3i0 (from t=0) for R=100Ω and r=5cm is given by 3π21n101010s.

D

Fro the same as in option (c), the time in which current in loop decreases to 10−3i0 (from t=0) for R=100Ω and r−5cm is given by 3π2106s.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A, C

Flux linked with loop due to its own magnetic field.
ϕ=μ0i2r(πr2)=μ0πri2
emf induced = −dϕdt=e=−μ0πr2Rdidt
∫ii0didt=−∫t02Rμ0πr⋅dt
i=i0e−2RT/μ0πt
Now, 10−3i0=i0e−2Rtμ0πr
which gives t=3π21n101010s.

Updated on:21/07/2023
|
Class 12PHYSICSMOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • What will be magnetic field at centre of current carrying circular loop of radius R?

    Aμ0I4πR
    Bμ0I2πR
    Cμ0I2R
    Dzero

  • A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
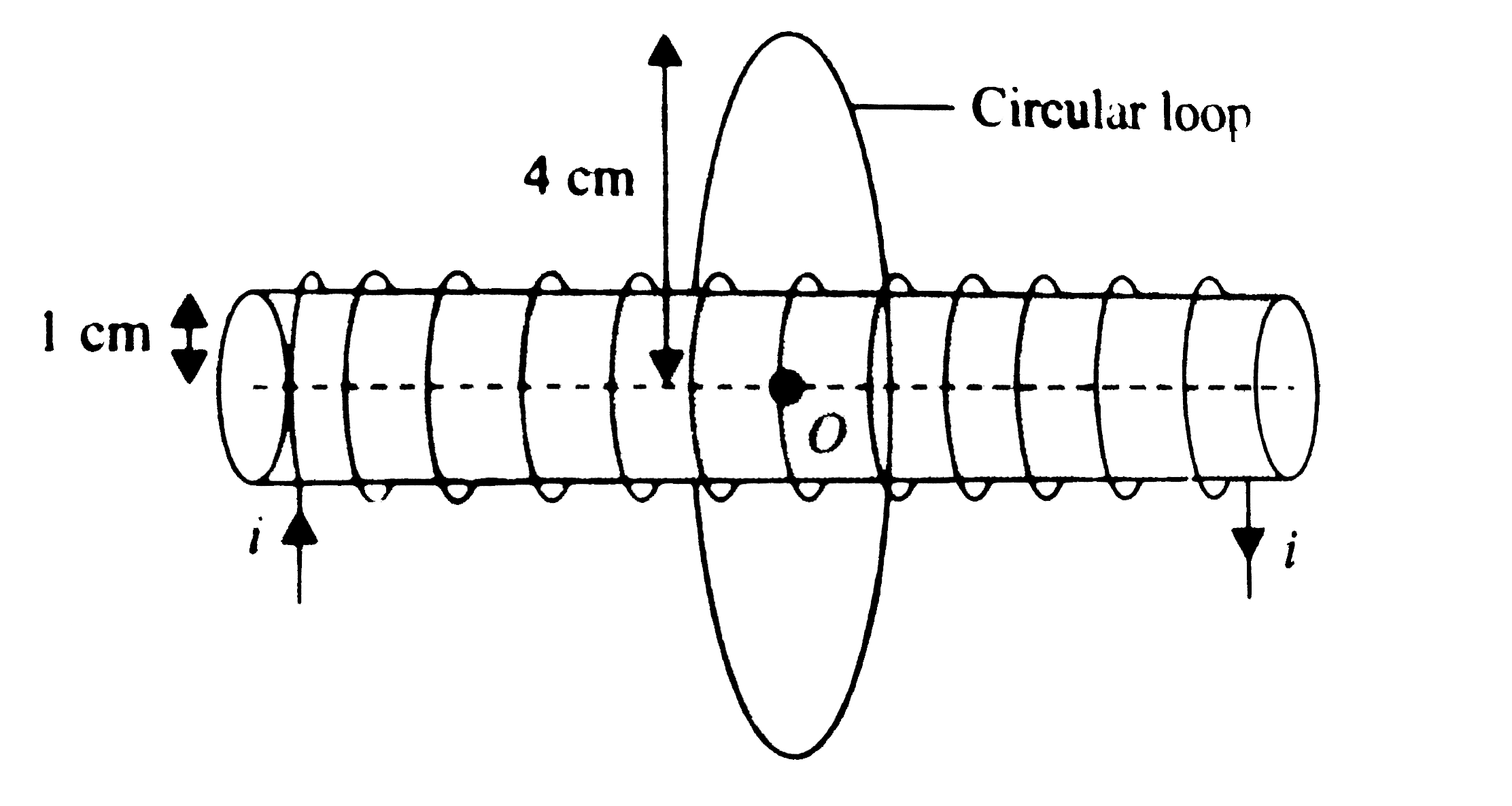
    ocr_image
    A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
    Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.

    A4.7×10−7Vm−1
    B3.82×10−6Vm−1
    C2.3×10−5Vm−1
    DNone of these

  • A current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
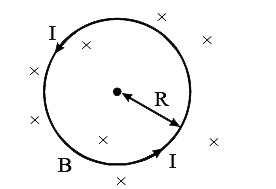    ocr_image

    ABIR
    B2πBIR
    CπBIR
    D2BIR