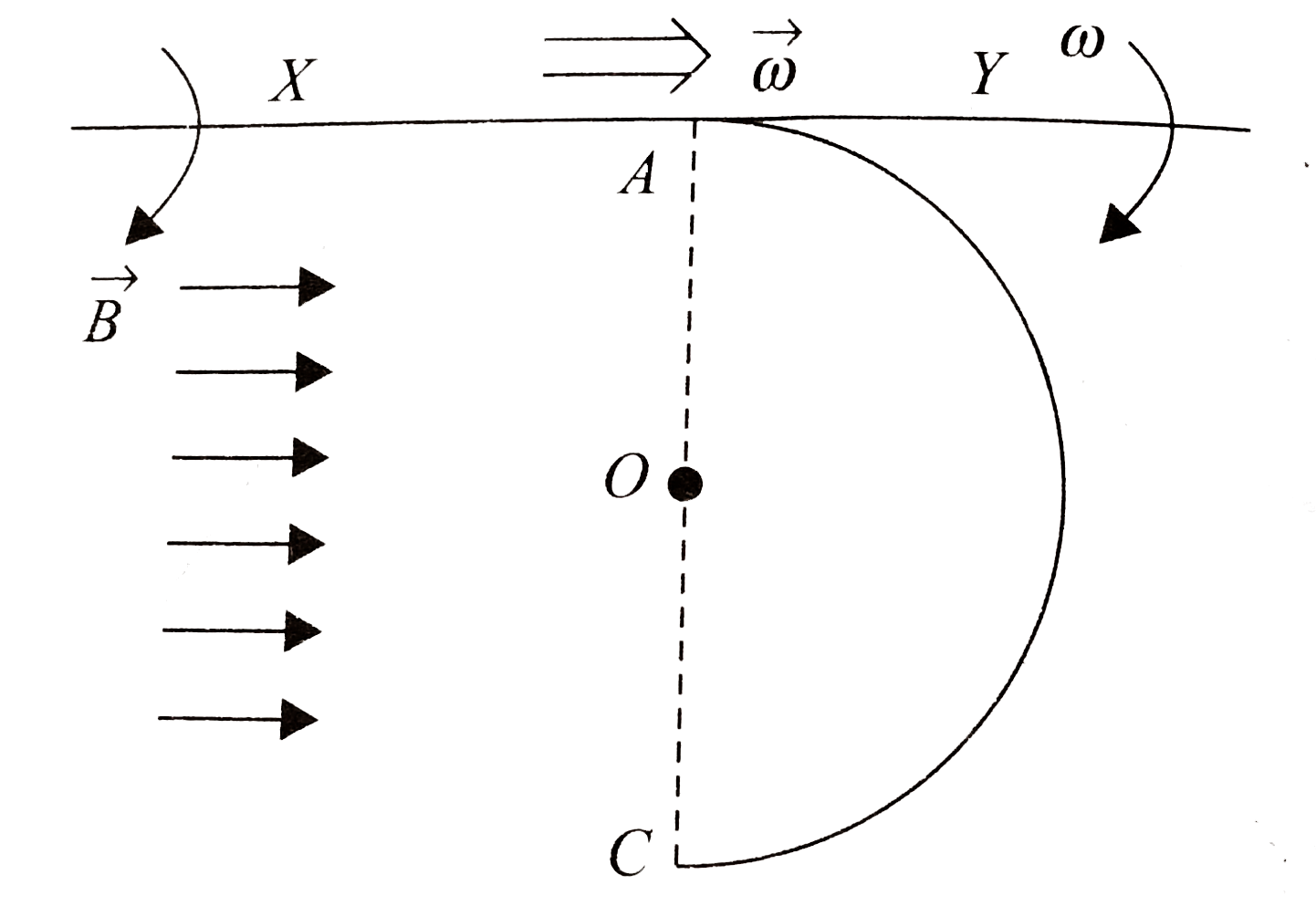
A thin wire AC shaped as a semi-circle of diameter d rotates with a constant angular frequency (ω) in a uniform magnetic field of indcution →B. The vector →ω is parallel to →B and the rotation axis XY passes through the end A of the wire and is perpendicular to the diameter AC (see Fig.). →B is directed left to right in the plane of the paper. The value of the line intergral I=∫→E⋅d→r taken along the wire form the point A to the point C will be ωBd2?. What interger should be inserted in place of question mark.
The correct Answer is:4
It is clear that the diameter AC traces out a circle as the given wire rotates about axis XY. The emf developed by induction between the ends A and C of the given semicircular wire is the sme as if a straight wire AC were rotating perpendicular to field B.
Hence flux linked =ϕB=B(12(AC)2θ)
where θ is the angle traced in time t.
By Faraday's law, the induced emf e=∮→E⋅d→l
But we also have , ∮E⋅dl=e=−dϕBdt
∮E⋅dr=−ddt(12(d)2θ)B
=−12d2B(dθdt)=−B2ωd2
But we desire only the ∫ACE⋅dr which will be 12 or ∮E⋅dr.
Hence ∮ACE⋅dr=−B2ωd2.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
A thin wire AC shaped as a semi-circle of diaameter d=20cm rotates with a constant angular velocity ω=100 rad/s in a unifrom magnetic field of induction B=5.0mT, with ω↑↑B. The rotation axis passes through the end A of the wire and is perpendicular to the diameter AC. Find the value of a line intergal ∫Edr along the wire from point A to C. Generalize the botained result.
View SolutionA copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View Solution
Knowledge Check
A conducting rod of length 2l is rotating with constant angular speed ω about is perpendicular bisector. A uniform magnetic field →B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
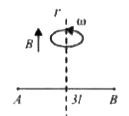 A12Bωl2B18Bωl2CZeroDBωl2
A12Bωl2B18Bωl2CZeroDBωl2When a 'J' shaped conducting rod rotating in its own plane with constant angular velocity omega, avout one of its end P, in a uniform magnetic field →B directed normally into the plane of paper) then magnetic of emf induced across it will be
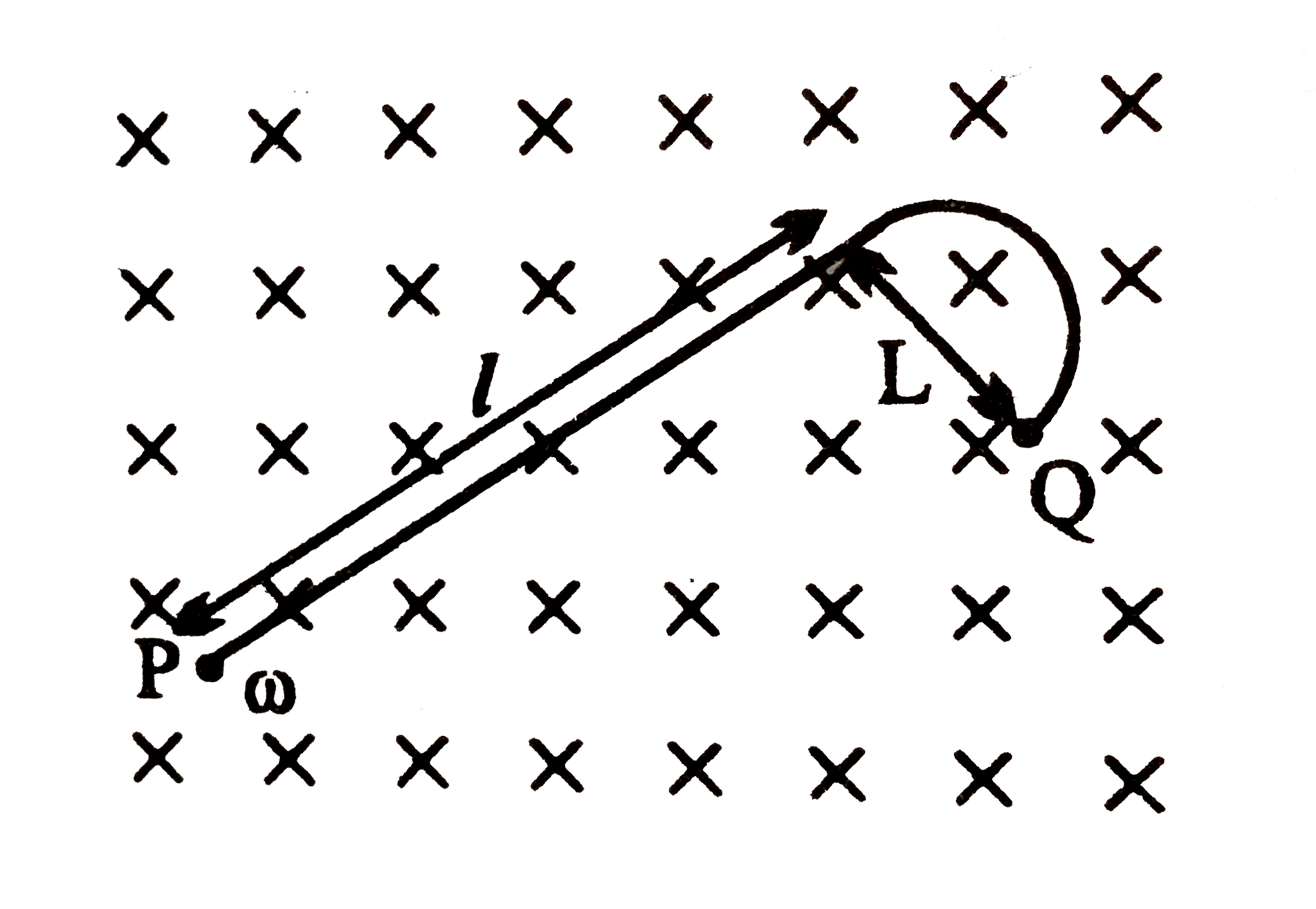 ABω√L2+l2B12BωL2C1Bω(L2+l2)D12Bωl2
ABω√L2+l2B12BωL2C1Bω(L2+l2)D12Bωl2
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
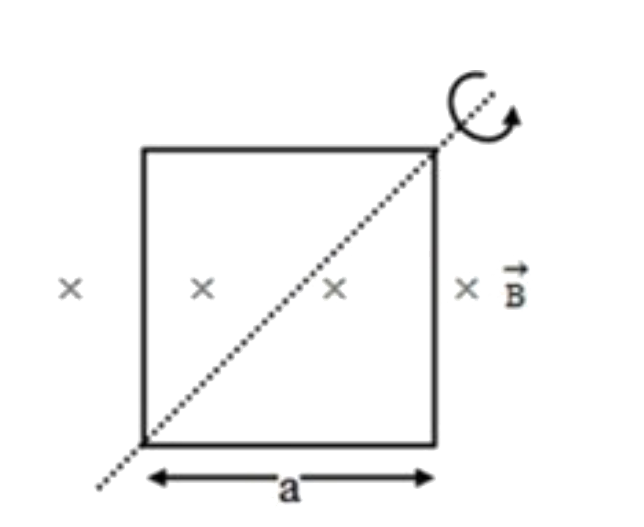
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is

View SolutionIf a vector →a is perpendicular to two non-collinear vector →b and →c , then →a is perpendicular to every vector in the plane of →b and →c .
View SolutionIf a vector →a is perpendicular to two non-collinear vector →b and →c , then →a is perpendicular to every vector in the plane of →b and →c .
View SolutionIf a vector →a is perpendicular to two non collinear vectors →b and →c, then →a is perpendicular to every vector in the plane of →b and →c
View Solution
