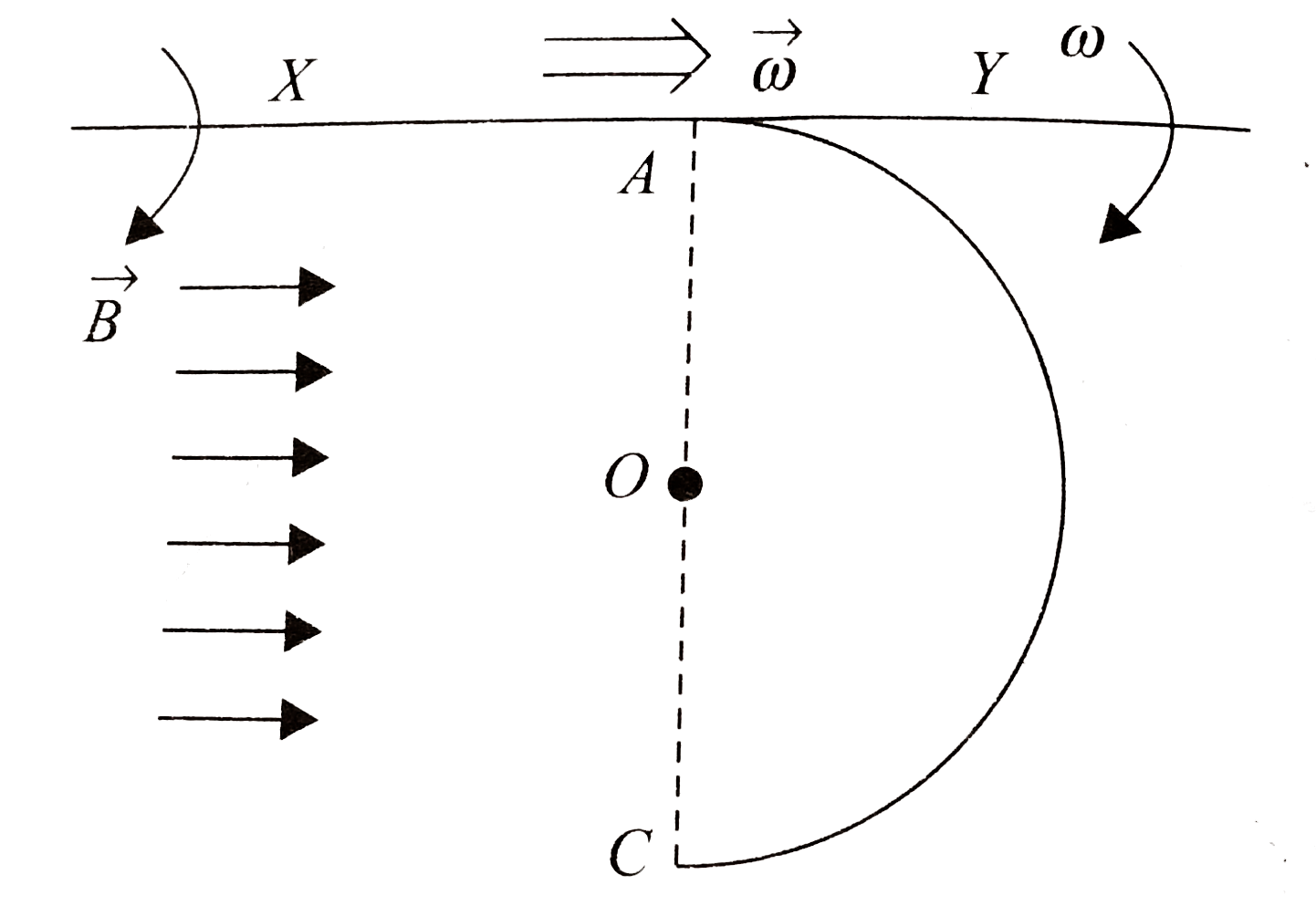
A thin wire AC shaped as a semi-circle of diaameter d=20cm rotates with a constant angular velocity ω=100 rad/s in a unifrom magnetic field of induction B=5.0mT, with ω↑↑B. The rotation axis passes through the end A of the wire and is perpendicular to the diameter AC. Find the value of a line intergal ∫Edr along the wire from point A to C. Generalize the botained result.
By definition,
→E=−(→v×→B)
So, ∫CA→E.d.→r=∫CA−(→v×→B).d→r=∫d0−vBdr
But, v=ωr, where r is the perpendicular distance of the point from A.
Hence, ∫CA→E.d.→r=∫d0−ωbBrdr=−12ωBd2=−10mV
This result can be gencralized to a wire AC of orbitary planner shape. We have
∫CA→E.d.→r=−∫CA(→v×→B).dr=−∫CA((ω×→r)×→B).d→r
=−∫CA(→B.→r.→ω−→B.→ω.→r).d→r
=−12Bωd2,
d being Ac and →r being measured from A.

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A thin wire AC shaped as a semi-circle of diameter d rotates with a constant angular frequency (ω) in a uniform magnetic field of indcution →B. The vector →ω is parallel to →B and the rotation axis XY passes through the end A of the wire and is perpendicular to the diameter AC (see Fig.). →B is directed left to right in the plane of the paper. The value of the line intergral I=∫→E⋅d→r taken along the wire form the point A to the point C will be ωBd2?. What interger should be inserted in place of question mark.
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View Solution
Knowledge Check
In the above problem, if the coil rotates with a constant angular velocity ω, the emf induced in it
A(a) is zeroB(b) changes non-linearly with timeC(c ) has a constant value =BanωD(d ) has a maximum value =BanωWhen a rod of length l is rotated with angular velocity of ω in a perpendicular field of induction B , about one end , the emf across its ends is
ABl2ωBBl2ω2CBlωDBlω2A wire shaped as a semicircle of radius a, is rotating about an acis PQ with a constant angular velocity ω=1√LC, with the help of an external agent. A uniform magnetic field B exists in space and is directed into the plane of the figure. (circuit part remains at rest) (left part is at rest)
 AThe rms value of current in the circuit is πBa2R√2LCBThe rms value of current in the circuit is πBa22R√2LCCThe maximum energy stored in the capacitor is π2B2a48R2CDThe maximum power delivered by the external agent is π2B2a44LCR
AThe rms value of current in the circuit is πBa2R√2LCBThe rms value of current in the circuit is πBa22R√2LCCThe maximum energy stored in the capacitor is π2B2a48R2CDThe maximum power delivered by the external agent is π2B2a44LCR
A semicircular wire of radius R= 20 cm rotates in its own plance about one end with angular velocity w=10rad/s in unifornm magnetic field B=5 mT perpendicular into the plane of the wire gtFind the voltage developend between the ends of the wire
View SolutionA copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
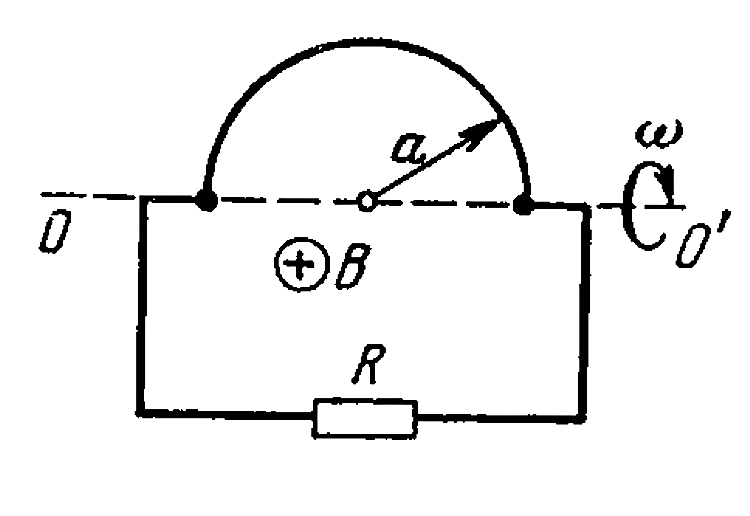
View SolutionA wire shaped as a semi-circle of radius a rotates about sn sxis OO' with an angular velocity ω in a unifrom magnetic field of induction B' (Fig). The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to R. NEglecting the magnetic field of the induced current, find the meand amount of thermal power being generated in the loop fueing a rotation period.
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA circular disc of radius 20 cm is rotating with a constant angular speed of 2.0rad/s in a uniform magnetic field of 0.2 T. Find the e.m.f. induced between the centre and rim of the disc. Given magnetic field is along the axis of rotation of disc.
View Solution
