An ideal gas (CpCv=γ) is taken through a process in which the pressure and volume vary as (p=aVb. Find the value of b for which the specific heat capacity in the process is zero.
(CpCv)=γ , Cp−Cv=R, Cv=Cp=0
pdv=1(b+1)(Rdt)
implies 0=(b+1)CvdT+(RdT)
implies 1(b+1)=−CvR
implies b+1=−RCv=−(Cp−Cv)Cv
= −γ+1
implies b=−γ
Topper's Solved these Questions
Similar Questions
An ideal gas is taken through a process in which pressure and volume vary as P=kV2. Show that the molar heat capacity of the gas for the process is given by C=Cv+R3.
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p=kv. Show that the molar heat capacity of the gas for the process is given by (C=Cv+R2.
View Solution
Knowledge Check
A monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
A5R3B35RC75RDR4Figure shows a process on a gas in which pressure and volume both change. The molar heat capacity for this process is C.
AC=0BC=CvCC>CvDC<Cv
An ideal monoatomic gas is taken through a process PVa = const. The value of 'a' for whichspecific heat capacity of the gas is zero is :-
View SolutionAn ideal gas is taken through a process in which the process equation is given as P=kVα, where k and α are positive constants. Find the value of α for which in this process molar heat capacity becomes zero.
View SolutionAn ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
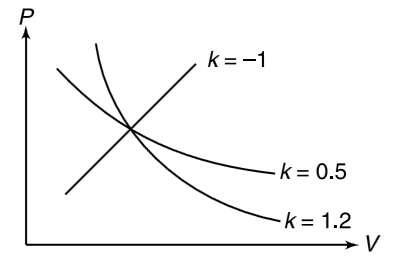
View SolutionFigure shows P versus V graph for various processes performed by an ideal gas. All the processes are polytropic following the process equation PVk= constant.
(i) Find the value of k for which the molar specific heat of the gas for the process is CP+CV2. Does any of the graph given in figure represent this process?
(ii) Find the value of k for which the molar specific heat of the gas is CV+CP. Assume that gas is mono atomic. Draw approximately the P versus V graph for this process in the graph given above.
View SolutionFor an ideal gas the ratio of specific heats is CpCv=γ. The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View SolutionAn ideal gas is made to undergo a process T=T0eαV where T0 and α are constants. Find the molar specific heat capacity of the gas in the process if its molar specific heat capacity at constant volume is Cv. Express your answer as a function of volume (V).
View Solution
