
A block A of mass m is placed on a smooth horizontal platform P and between two elastic massless springs S1 and S2 fixed horizontally to two fixed vertical walls. The elastic constants of the two springs are equal to k and the equilibrium distance between the two springs both in relaxed states is d. The block is given a velocity v0 initially towards one of the springs and it then oscillated between the springs. The time period T of oscillations and the minimum separation dm of the spring will be
T=2(dv+π√mk),dm=d
T=2(dv+2π√mk),dm=d−v√mk
T=2(dv+2π√mk),dm=d−2v√mk
T=2π√mk,dm=d
The correct Answer is:A
The oscillation of the block will be periodic but not simple harmonic. The springs are only comressed but not extended since the block loses contact with either spring just in its relaxed state. The minimum distance between the springs will therefore be when both the springs are relaxed i.e., during the interval when the block moves between the springs.
Time taken by the block to move from one either spring is
t2=12[2π√mK]=π√mK
Hence the periodic time T of the oscillation of the block is T=2(t1+t2)
=2[dv+π√mK]
Also minimum distance between the springs=d.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective21videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
 View Solution
View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m=25kg on a smooth horizontal surface with a velocity →v=3ms−1 meets the spring of spring constant k=100N/m fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are.
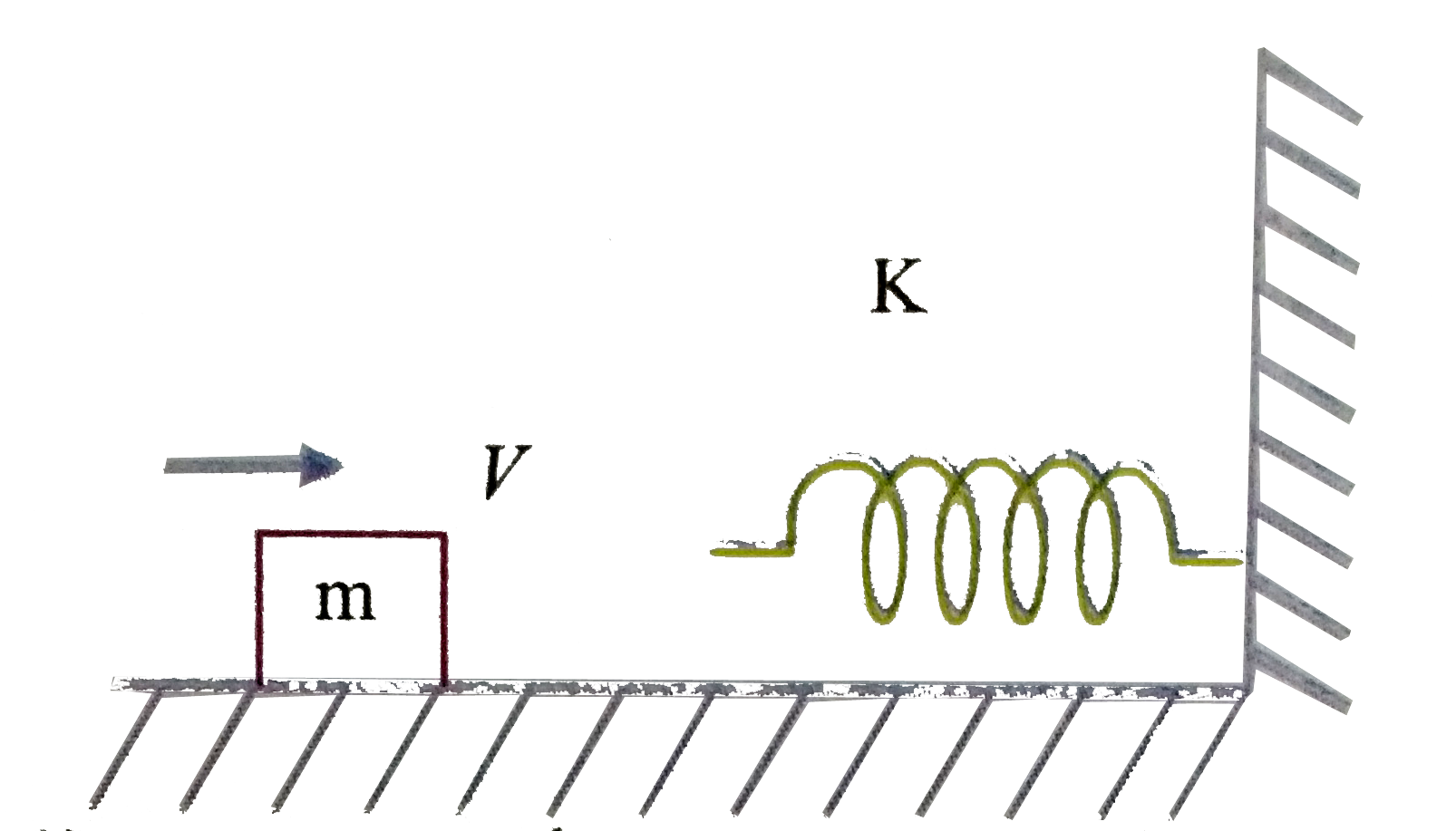 .A1.5m,−3ms−1B1.5m,0ms−1C1.0m,3ms−1D0.5m,2ms−1
.A1.5m,−3ms−1B1.5m,0ms−1C1.0m,3ms−1D0.5m,2ms−1 - Question 2 - Select One
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0 - Question 3 - Select One
A block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
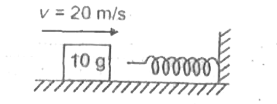 A2 mB0.2 mC20 mD43m
A2 mB0.2 mC20 mD43m
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :
 View Solution
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :
 View Solution
View SolutionA smooth wedge of mass m and angle of inclination 60∘ rests unattached between two springs of spring constant K and 4k on a smooth horizontal plane both springs in the unextended position the time period of small oscillation of the wedge (assuming that the springs are constrained to get compressed along their length) equals
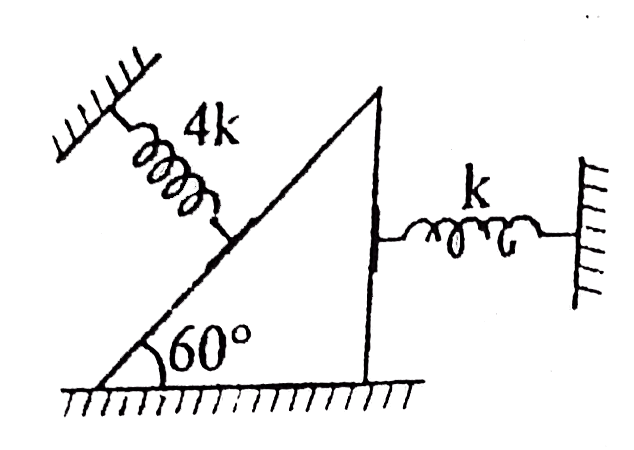 View Solution
View SolutionA block P of mass m is placed on horizontal frictionless plane. A second block of same mass m is placed on it and is connected to a spring of spring constant k, the two blocks are pulled by distance A. Block Q oscillates without slipping. What is the maximum value of frictional force between the two blocks.
 View Solution
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution

