In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A particle of mass m is released from height 4.5mg/k from 2m . The particle stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.
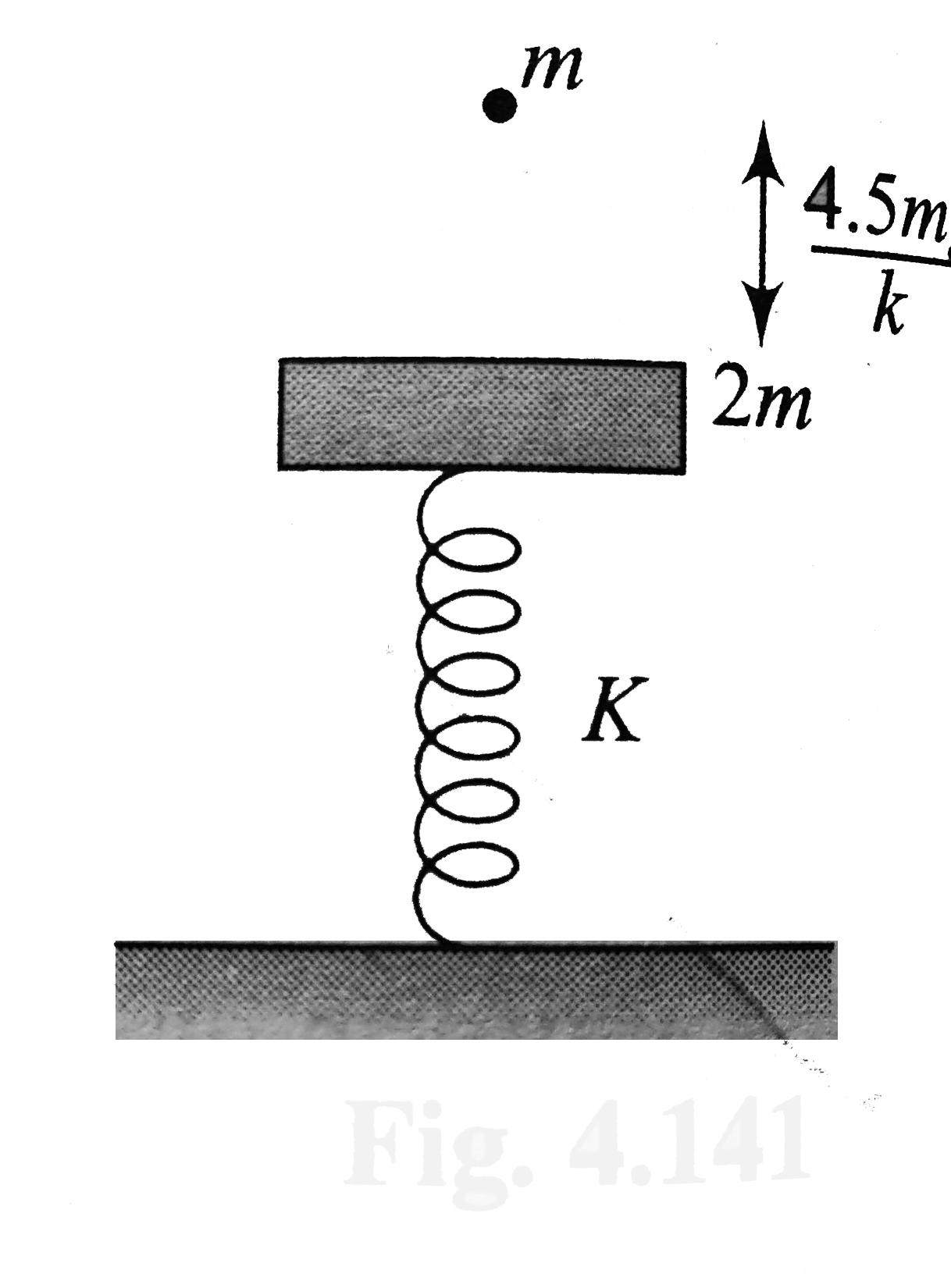
Velocity of the particle just before collision.
u=√2g×4.5mgK⇒u=3g√mK
Now it collides with the plate.
Now just after collision velocity (V) of the system of plate + particle'
mu=3mV⇒V=u3=g√mK
Now the system performs SHM with time period
T=2π√3mKω=√K3m and mean position as mgK
distance below the point of collision.
Let the equation of motion is
y=Asin(ωt+ϕ) .(i)
v=dydt=Aωcos(ωt+ϕ) ..(ii)
At t=0,y=mgK and v=g√mK
From eqs (i) and (ii) mgK=Asinϕ ..(iii)
A=2mgK ..(iv)
From Eqs. (iii) and (iv), ϕ=5πK y=2mgKsin(√K3mt+5π6)
Hence equation of SHM should be
y=−A=−2mgK=2mgKsin(√K2mt+5π6)
The plate will be at rest again when
y=−A=−2mgK=2mgKsin(√K3m+5π6)
⇒sin(√K3mt+5π6)=−1=sin(3π)2
⇒√K3mt+5π6=3π2⇒=2π3√3mK
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type2videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension33videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A partical of mass m is released from height 4.5mg/k from 2m . The partical stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.
 View Solution
View SolutionIn the figure shown mass 2m is at rest and in equilibrium. A particle of mass m is released from height 4.5mgk from palte. The particle sticks to the plate. Neglecting the duration of collision. Starting form the when the particles sticks to plate to the time when the spring is in maximum compression for the first time is 2π√mak then find a.
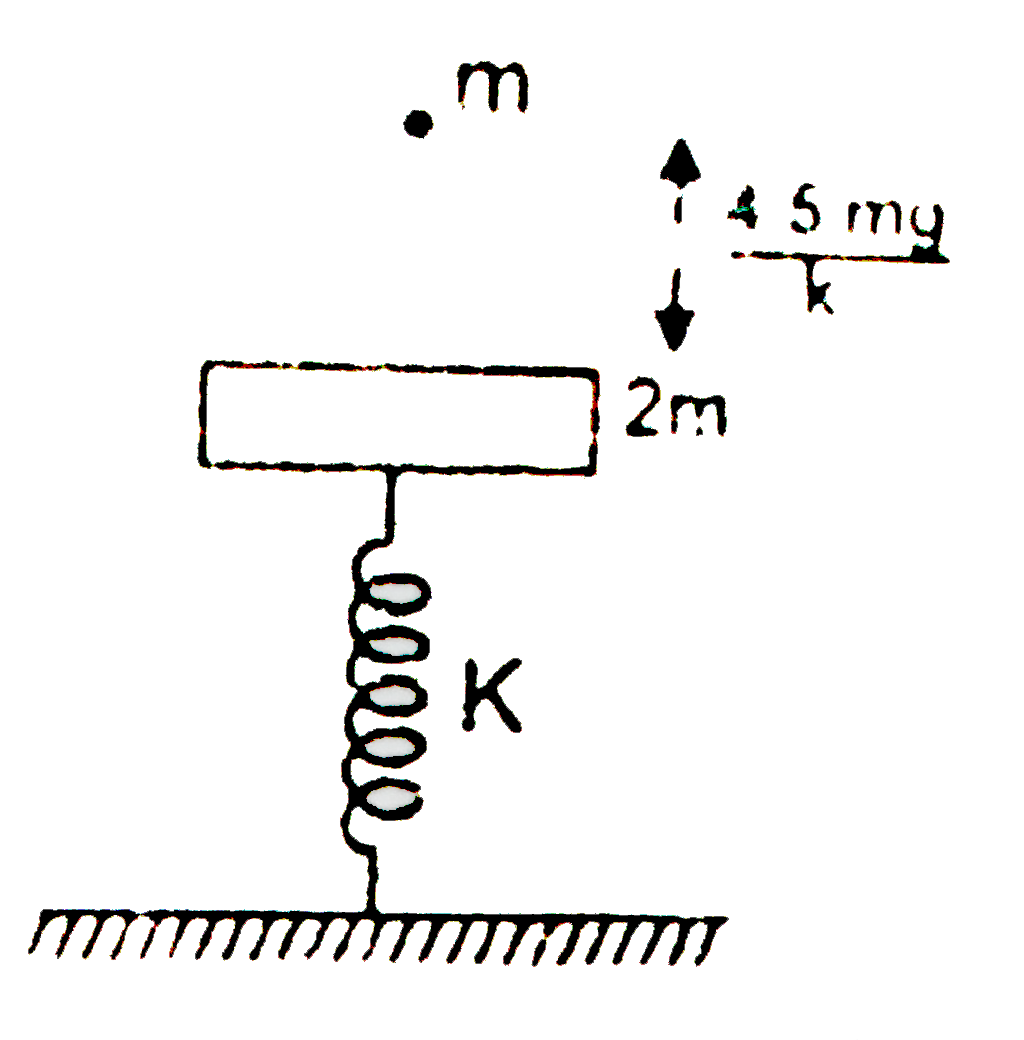 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is released from rest and follows a particle as a function of time?
 A
A B
B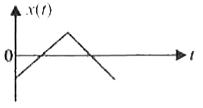 C
C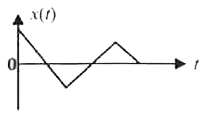 D
D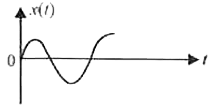
- Question 2 - Select One
A block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
A2B3C4D1 - Question 3 - Select One
A 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)
 AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
The block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
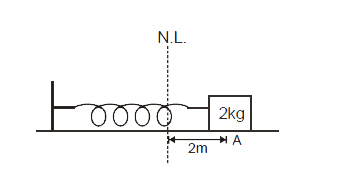 View Solution
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
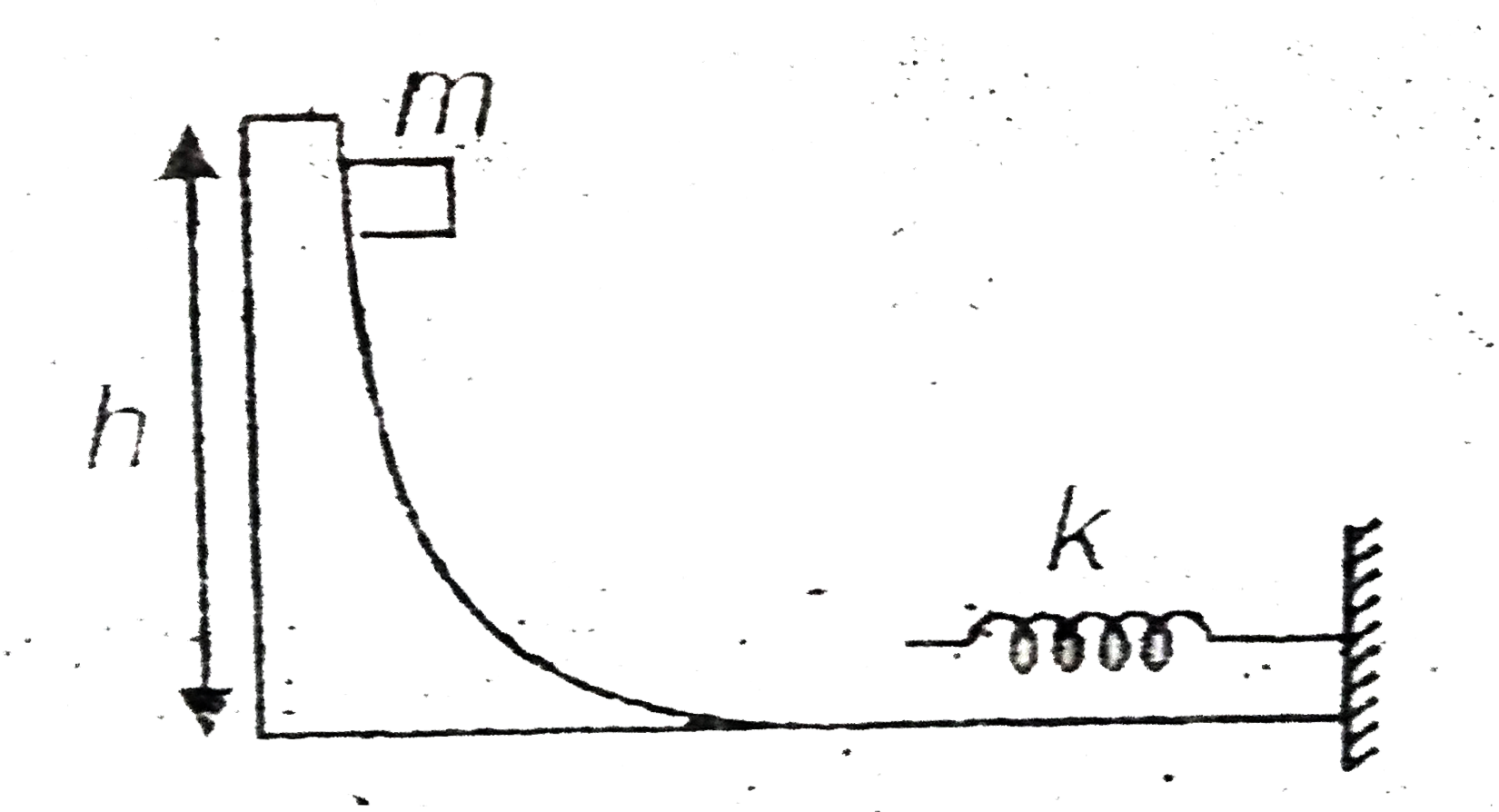 View Solution
View SolutionA block of mass 200 g is suspended by a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g=10m/s2.
 View Solution
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
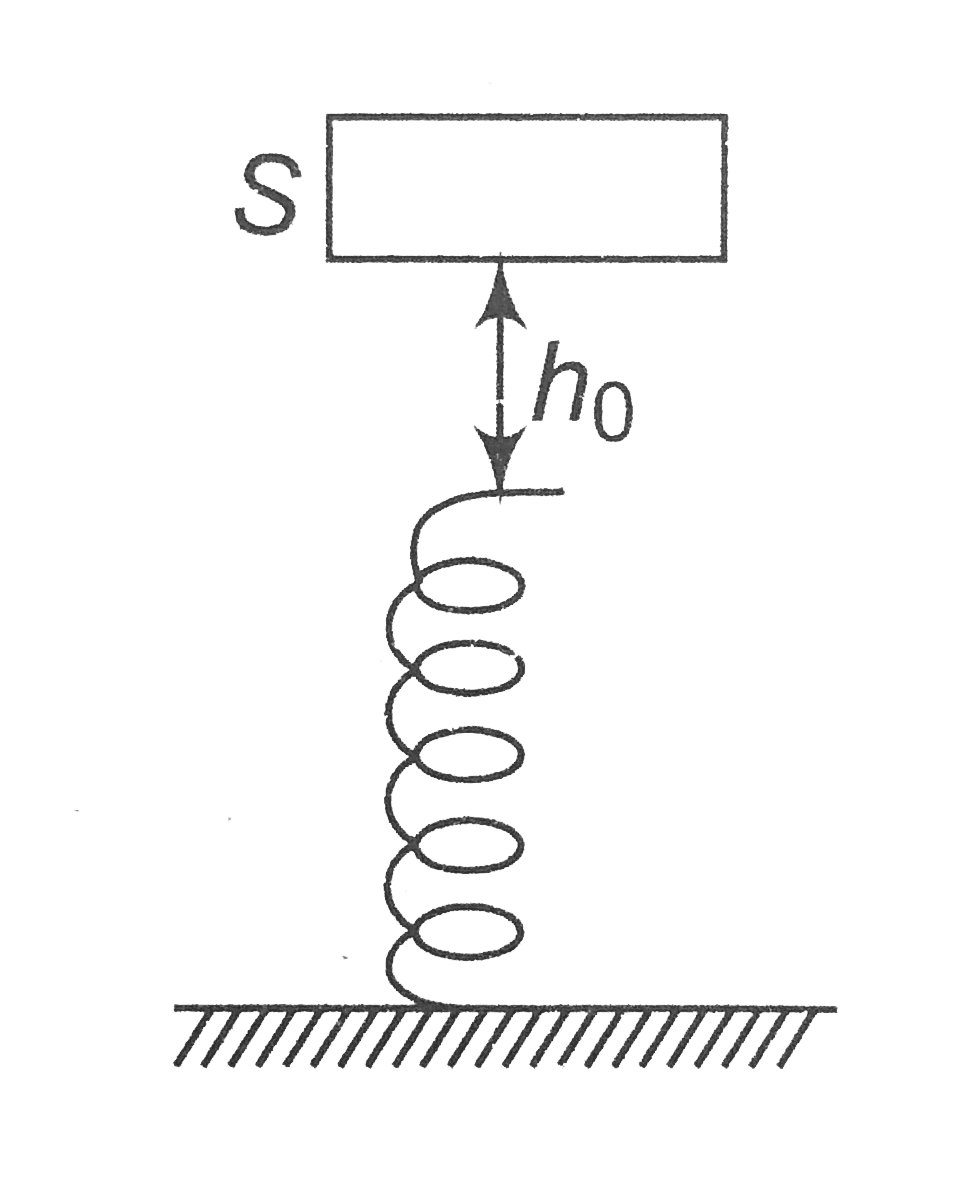 View Solution
View Solution

