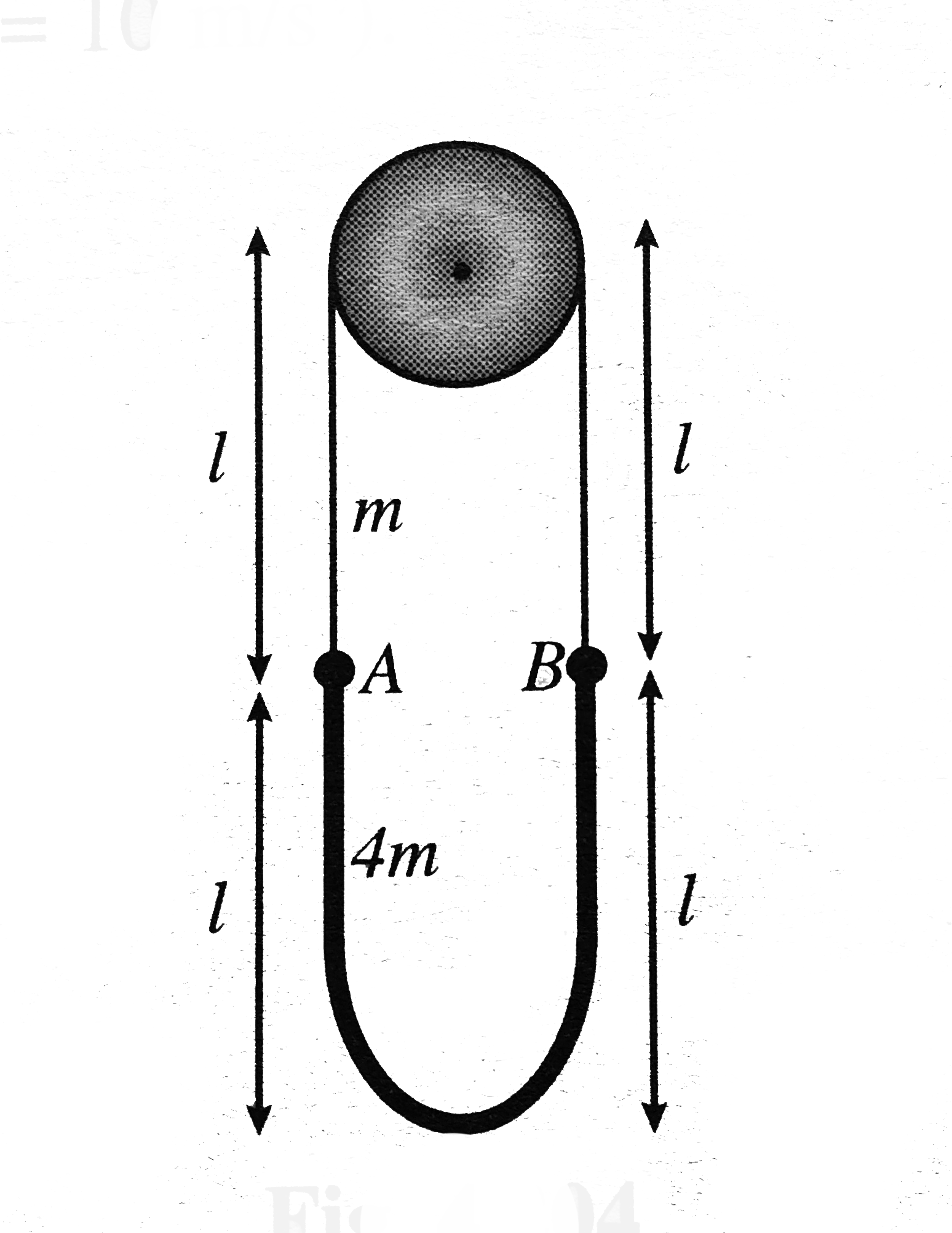
Two uniform ropes having linear mass densities m and 4m are joined to form a closed loop. The loop is hanging over a fixed frictionless small pulley with the lighter rope above as shown in the fig. (in the figure equilibrium position is shown). Now if point A (joint) is slightly displaced in downward direction and released, it is found that the loop performs SHM with the period of oscillation equal to N. Find the value of N (take l=150m4π2,g=10ms2).
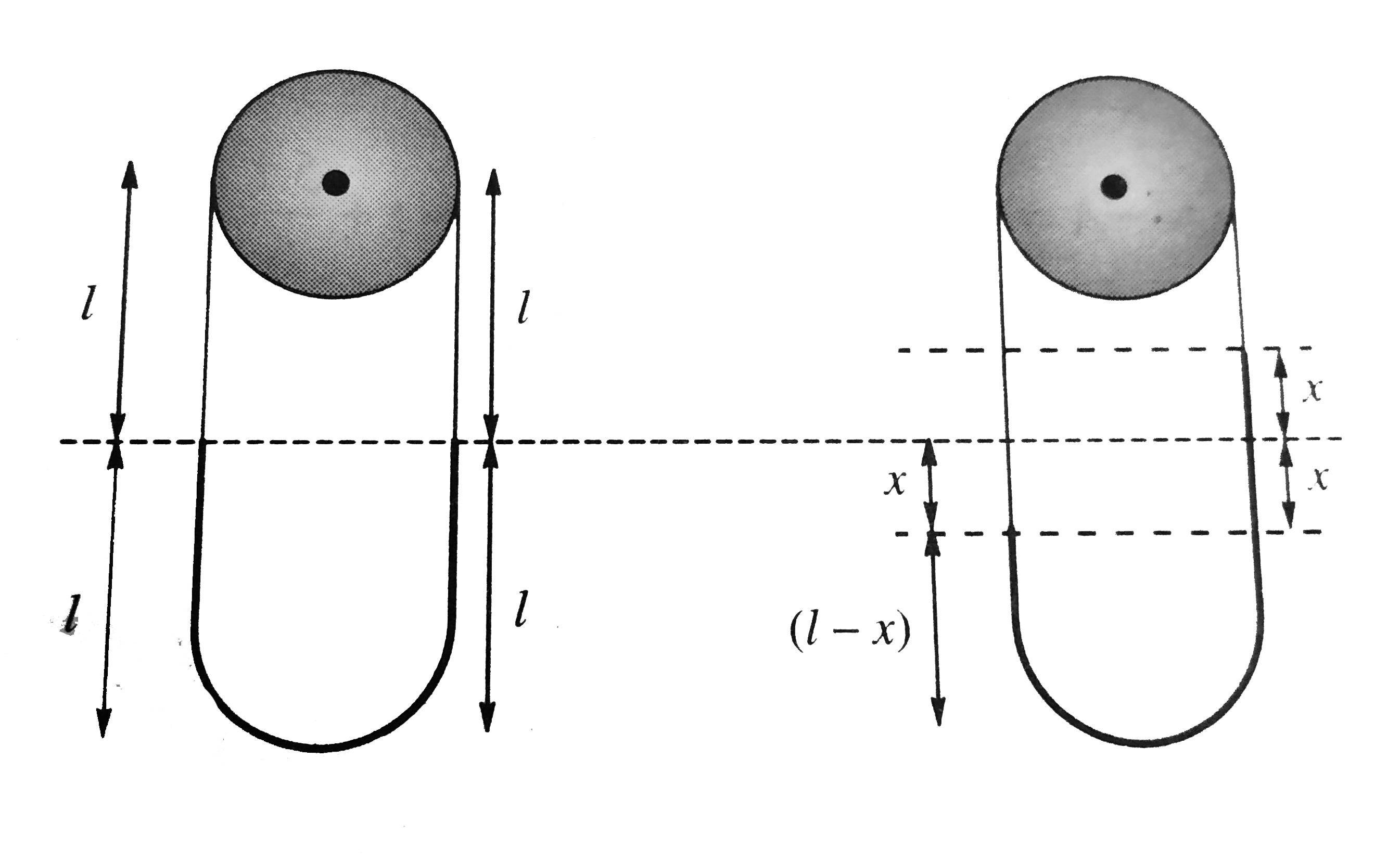
Let point B is displace in the downwards direction by x. Net imbalance forces =mtotal.a
[4mg(l+x)+mg(l−x)−{4m(l−x)g+m(l+m)g}]
=(4m×2l+m×2l)a
a=−(3g5l)x
ω=√mg5l⇒T=2π√5l3g=5s
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Two blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
View SolutionA charged particle of mass m having charge q remains in equilibrium at height d above a fixed charge Q. Now the charged particle is slightly displaced along the line joining the charges, show that it will executes S.H.M. and find the time period of oscillation.
View Solution
Knowledge Check
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)A block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionA uniform plank of length l and mass m is balanced on a fixed semi-circular plate of radius R as shown in the figure. If the plank is tilted slightly from its equilibrium position, and released, prove that it will execute S.H.M find the period of its oscillation.
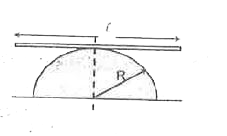
View SolutionConsider a situation shown in the figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute S.H.M. calculate the time period.

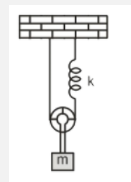
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is
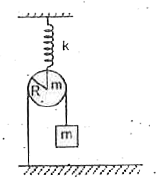
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
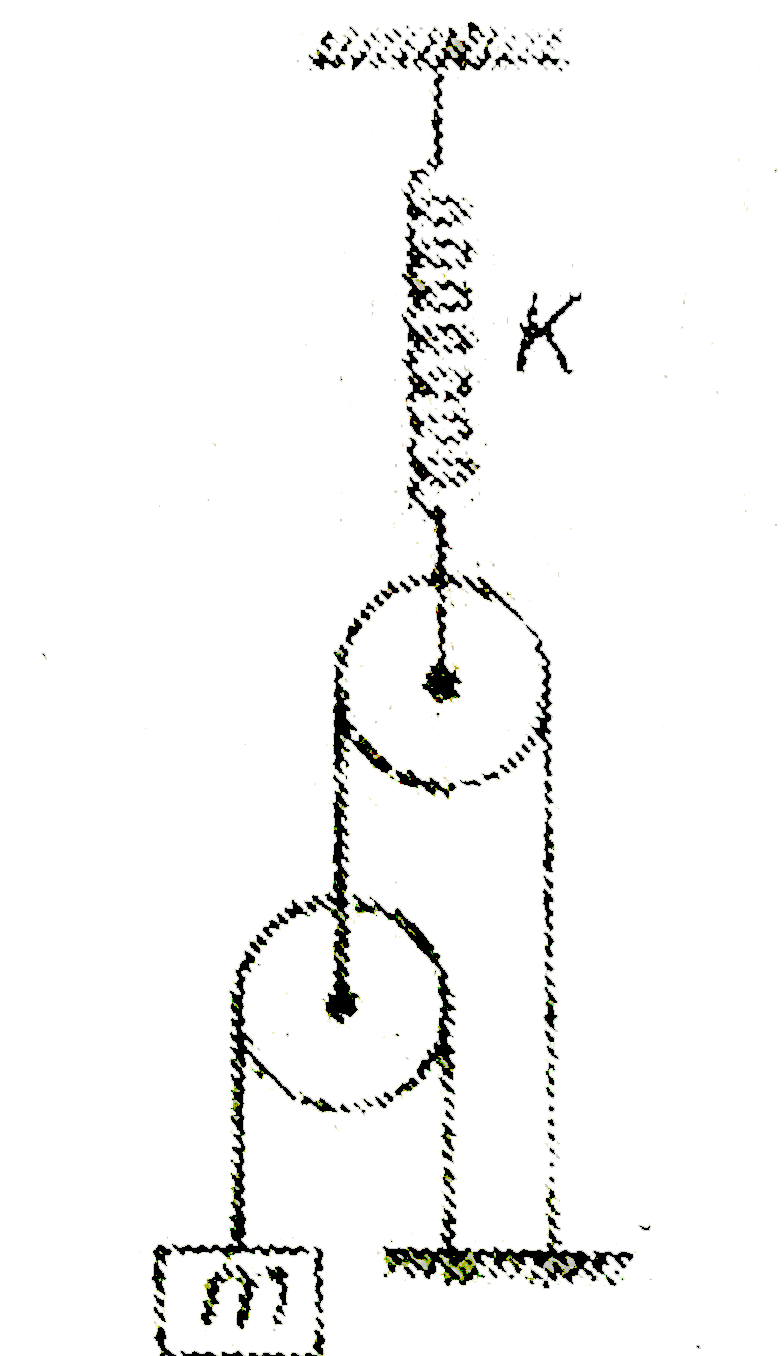
View Solution
