A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is u. If a small transverse disturbance is produced at a point of the loop, with what speed (relative to the string) will this disturbance travel on the string ?

Text Solution

Verified by Experts

m=mass per unit length of the string.
R=Radius of the loop
w=angular velocity
V=Linear velocity of the string

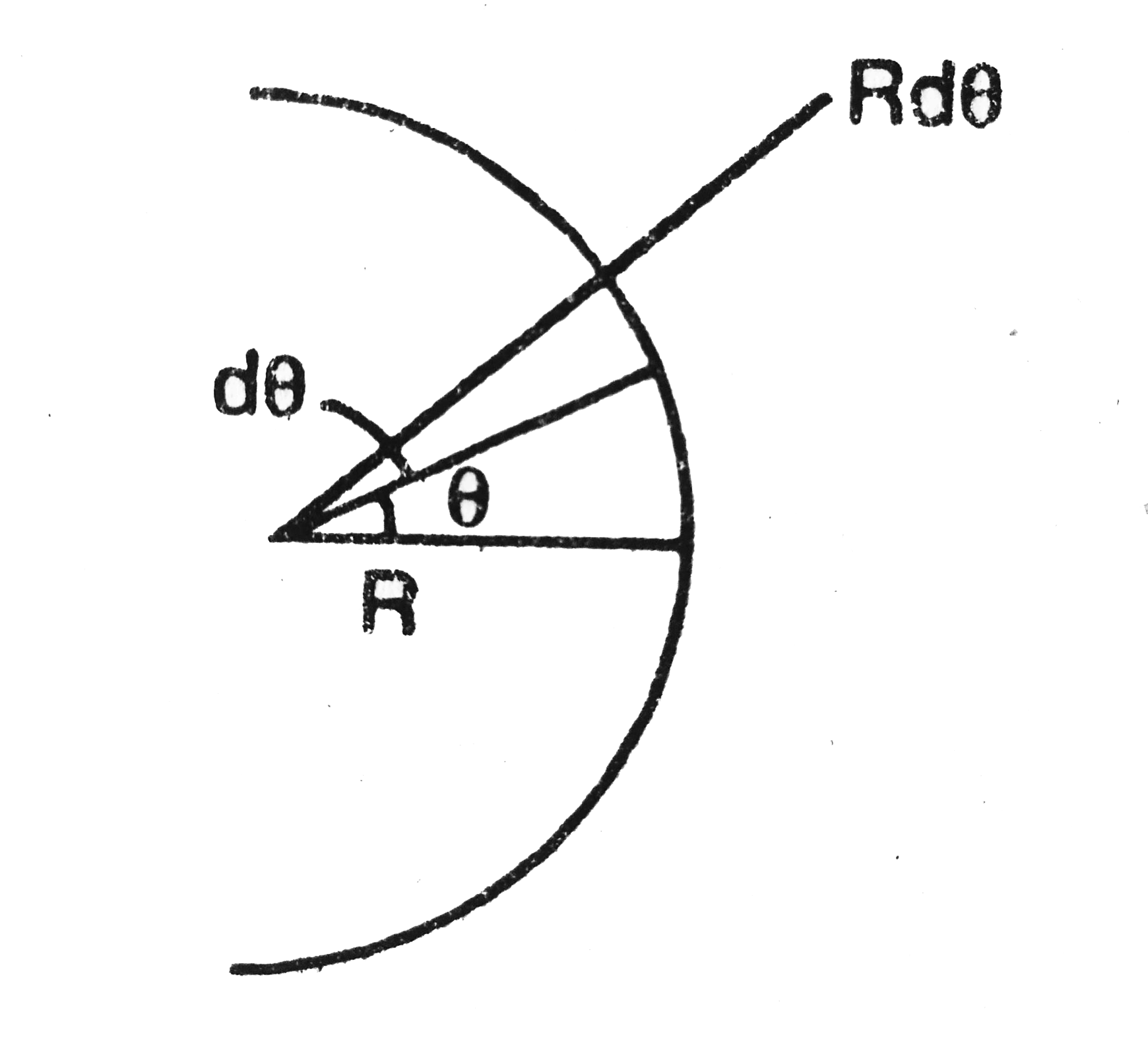
consider one half of the string as shown in ure.
The hal loop experiences centrifugl force at every point, away from centre, which ils balanced by tension 2T.
Consider an elemennt of angular part $d t h η$ at angle $θ . c o n s r a \neg h e r e \leq m e n t s y m m e t r i c \to t h i s . C e n r if u g a l f or c e exp e r i e n c e b y t h e e \leq m e n t$ =(mRdtheta)w^2R $$ (......Length of element =Rdtheta, mass =mRdtheta)
Resolving in to rectangular components, net force on the two symmetirc elements,
dF=2mR^2dthetaw^2sintheta $ [H or i z o n t a l c o m p o \neq n t s c n c e l s e a c h o t h e r] s o, \to t a l$ F=int_0^(pi/2)2mR^2omega^2sithetadtheta $$ =2mR^2omega^2[-costheta] $$ =2mR^2w^2 $$ Again 2T=2mr^2w^2 $$ rarr T=mR^2w^2 $ v e l o c i t y o f t r a n s v e r s e v i b r a t i o n $ V=sqrt((T/m)) $$ =sqrt((mR^2omega^I2)=omegaR=V

A string of mass M as a circular loop rotates abot its axis on a frictionless horizontal plane at a uniform rate so that the tangential plane at a uniform rate so that the tangential speed of any particle of the string is $v$ . If a small transverse disturbance is produced at a point of the loop, then speed (relative to the string) of disturbance on the string is
A $v \sqrt{\frac{M}{2}}$
B $\sqrt{2} v$
C $v$
D $\frac{v}{\sqrt{2}}$
A loop of a string of mass per unit length $μ$ and radius R is rotated about an axis passing through centre perpendicular to the plane with an angular velocityco. A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance for a stationary observer is :
A $ω R$
B $2 ω R$
C $3 ω R$
DZero
A loop of a string of mass length $μ$ and redius R is rotated about an axis passing through centre perpendicular to the plane with an angular velocity $ω$ .A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance observer is
A $ω R$
B $2 ω R$
C $3 ω R$
DZero