The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.

Determine the tension in the string.
25/3N
25/7N
5N
25/9N
The correct Answer is:d
The waves is travelling along the positivex-axis
∴y=Asin[kx−ωt+ϕ]
at x=0,y=Asin[−ωt+ϕ]
Also, at t=0,y=Asinϕ=A/2,
sinϕ=1/2
⇒ϕ=(π/6),(5π/6),…
and at t=0.05s,y=Asin(−ω20+ϕ)=0
or, −ω20+ϕ=0,π,2π,...
For t=0.05s and x=1m,
y=Asin(k−ω20+ϕ)=0
since, λ=2m
∴π−ω20+ϕ=0,π,2π,...
from Eqs. (i),(ii) and (ii), we get
ϕ=π/6
ϕ−ω20=0
ω=10π3
f=ω2π=53Hz
velocity of wave is
V=λf=(2)(5/3)=10/3m/s
Maximum velocity of the particle is
Vmax=oemgaA)10π/3))(10x10−3)=π/30m/s
Tension in the string is
T=μV2=(0.25)(10/3)2=25/9N.
the equation of the wave is
y=10sin[πx−(10/3)πt+(π/6)]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning6videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A piano string having a mass per unit length equal to 5.00×103kg/m is under a tension of 1350N, Find the speed with which a wave travels on this string.
View SolutionTwo strings A and B are connected together end to end as shown in the figure. The ratio of mass per unit length μBμA=4. The tension in the string is same. A travelling wave is coming from the string A towards string B. if the fraction of the power of the incident wave that goes in sting B is n9 the value of n is:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
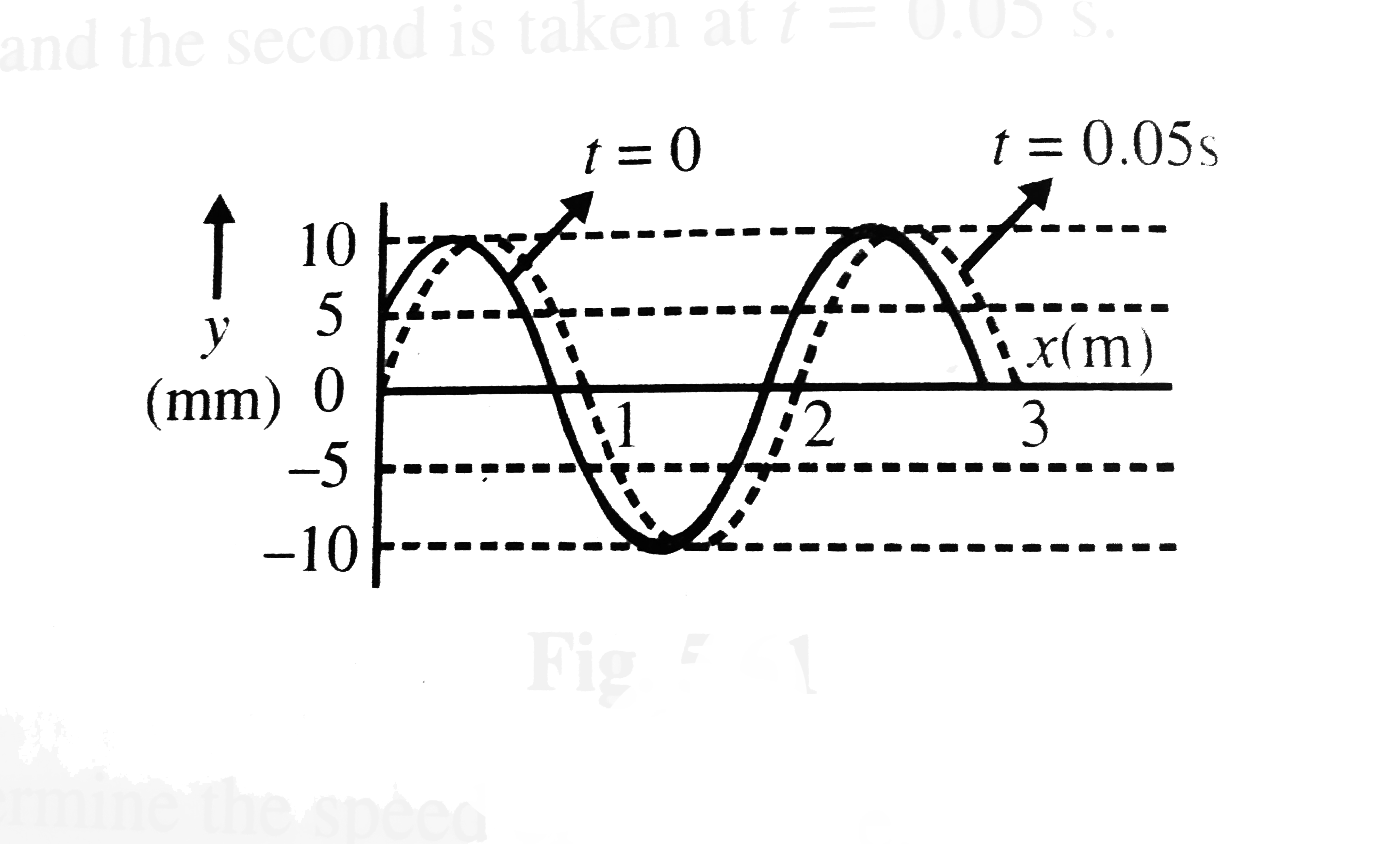
Determine the equation of the wave.Ay10sin2πx−10/3πtπ/6Byπ10sinππx−π10/3ππtπππ/3ππCyπ10sinππx−π10/3ππtπππ/6ππDyπ10sinππx−π5/3ππtπππ/3ππ - Question 2 - Select One
The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
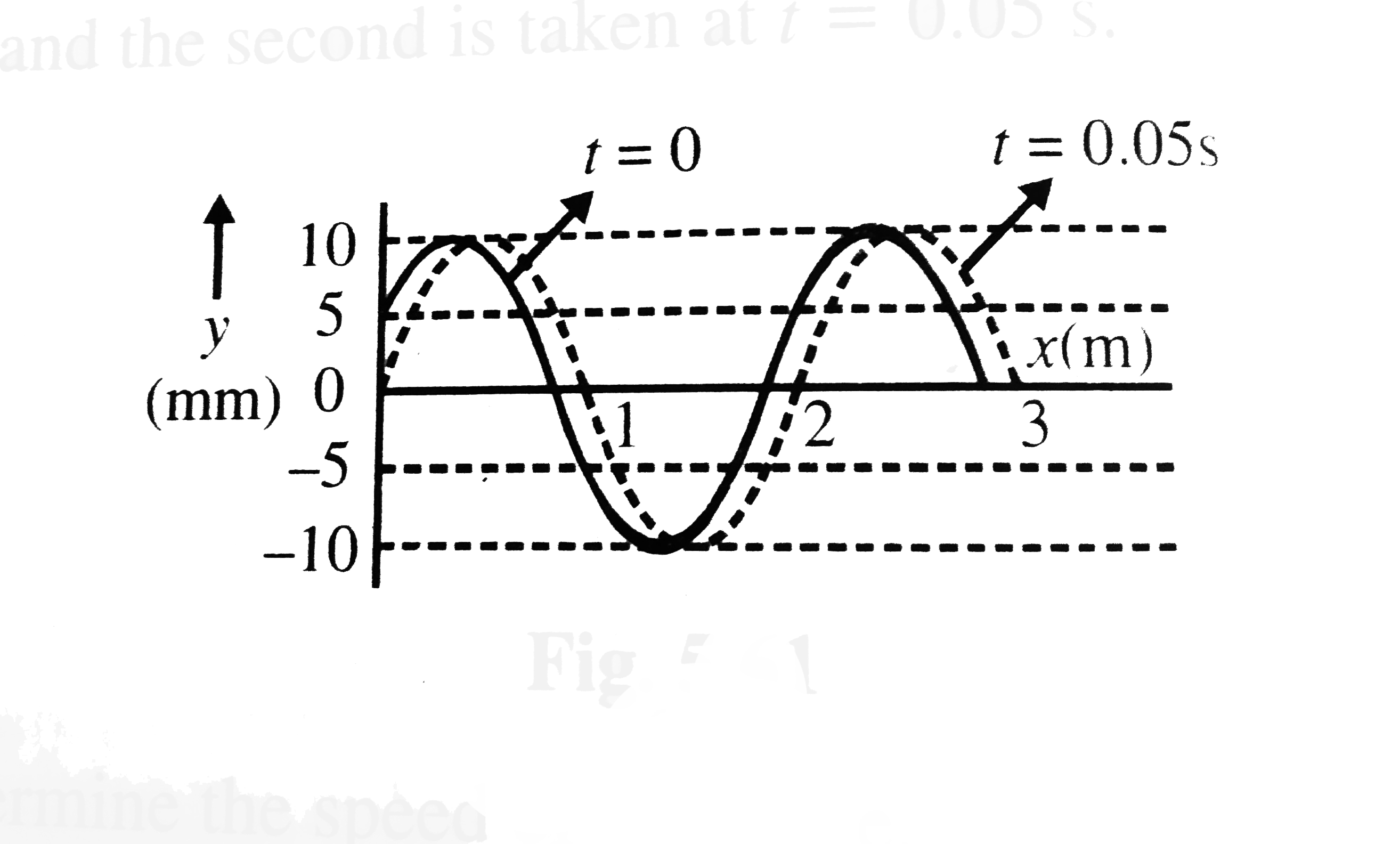
Determine the frequency of the wave.A5/3HzB10/3m/sC5HzD10Hz - Question 3 - Select One
The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
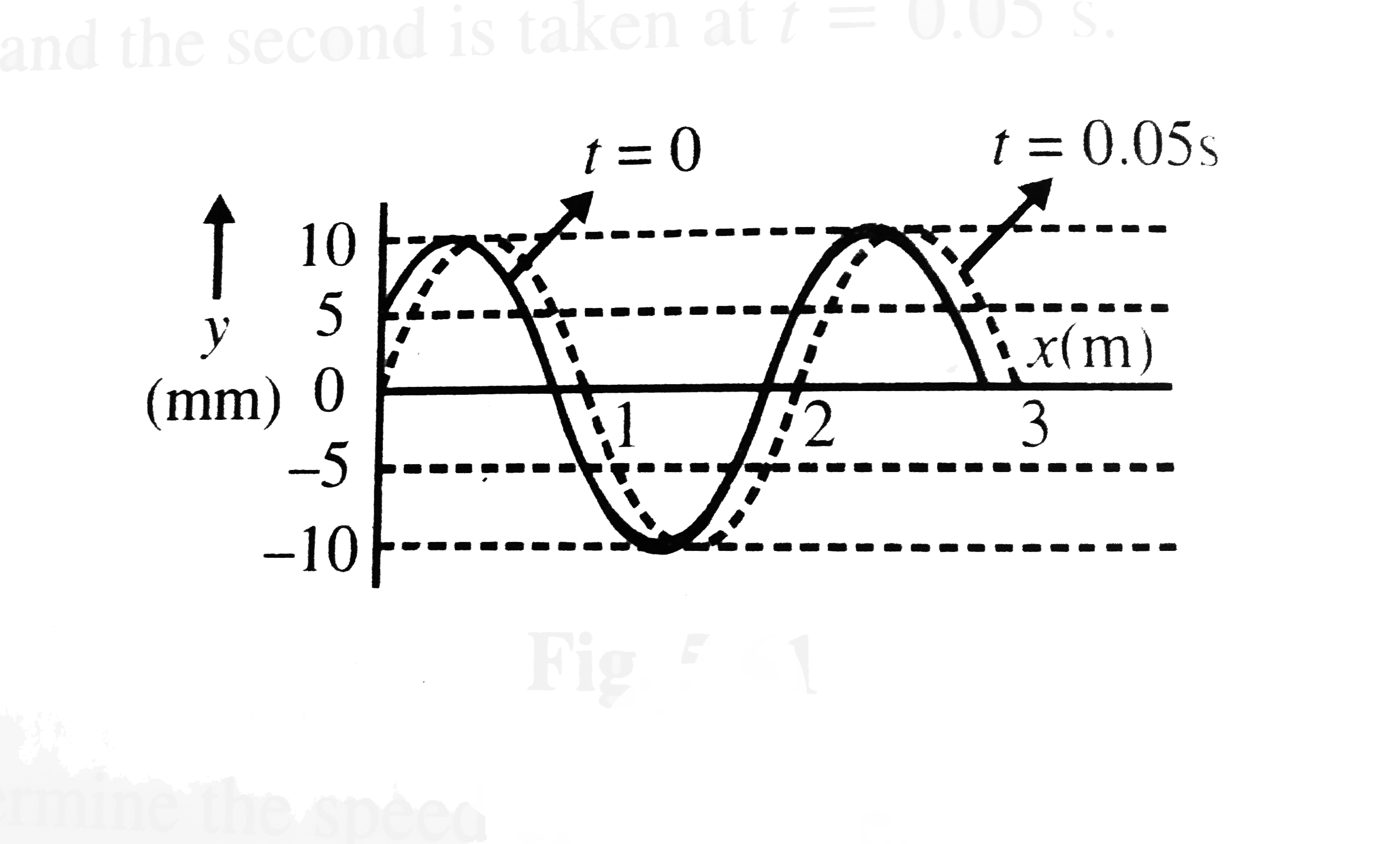
Determine the speed of the wave.A20/3m/sB10/3m/sC20m/sD10m/s
The transverse displacement of a string (clamped at its two ends ) is given by
y(x,t)=0.06sin(2π3)xcos(120πt)
wherer x ,y are in m and t ini s. The length of the string is 1.5m and its mass is 3×10−2 kg. Answer the following: (i) Does the function represent a travelling or a stationary wave ?
(ii) Interpret the wave as a superimposition of two waves travelling in opposite directions. What are the wavelength, frequency and speed of propagation of each wave ?
(iii) Determing the tension in the string.View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
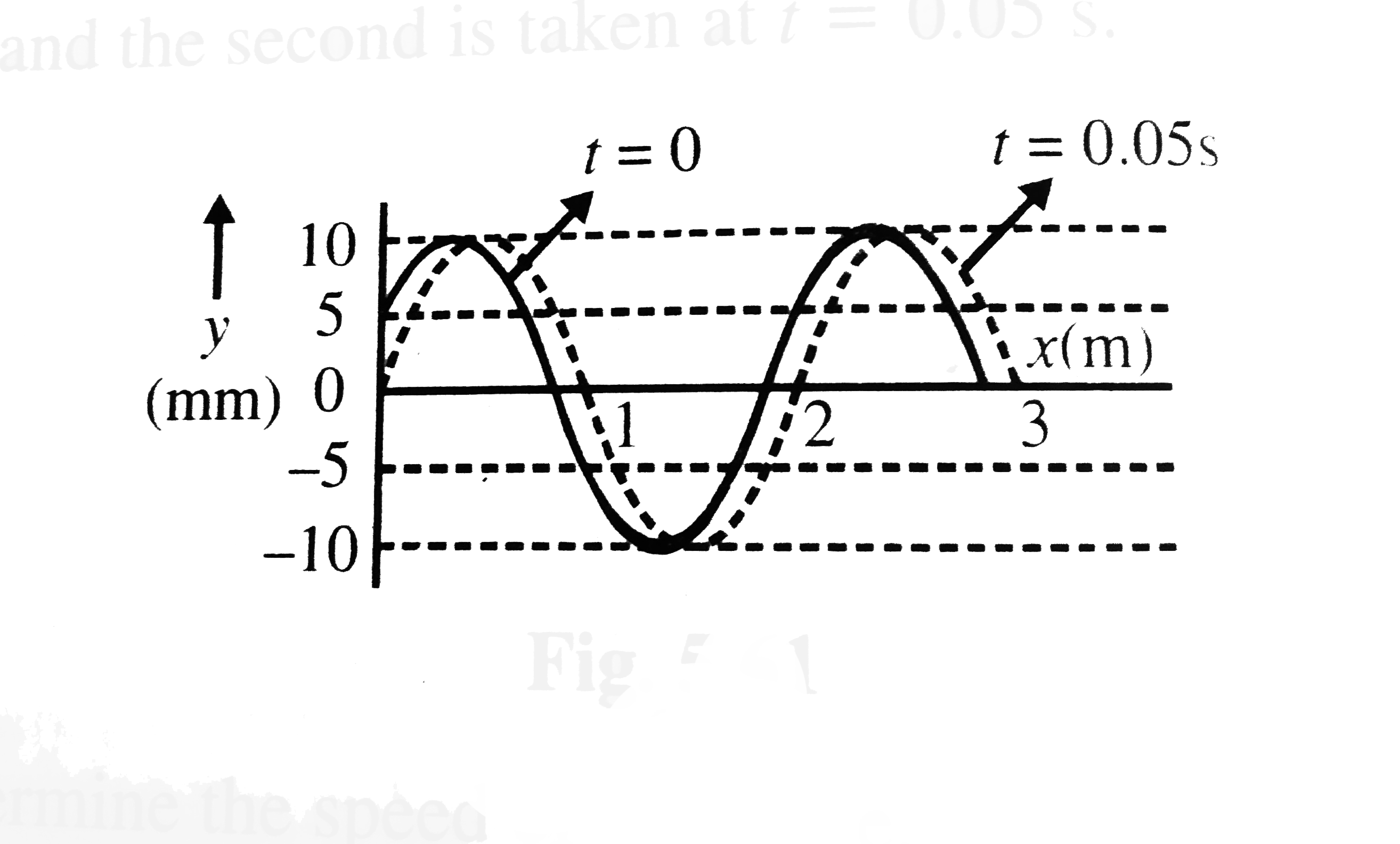
Determine the maximum speed of the particle.View SolutionA transverse periodic wave on a string with a linear mass density of 0.200kg/m is described by the following equation
y=0.05sin(420t−21.0x)
where x and y are in metres and t is in seconds. Tension in the string isView SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA transverse periodic wave on a string with a linear mass density of 0.200 kg/m is described by the following equation y=0.05sin(420t−21.0x)
where x and y are in metres and t is in seconds.The tension in the string is equal to :View Solution

