The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
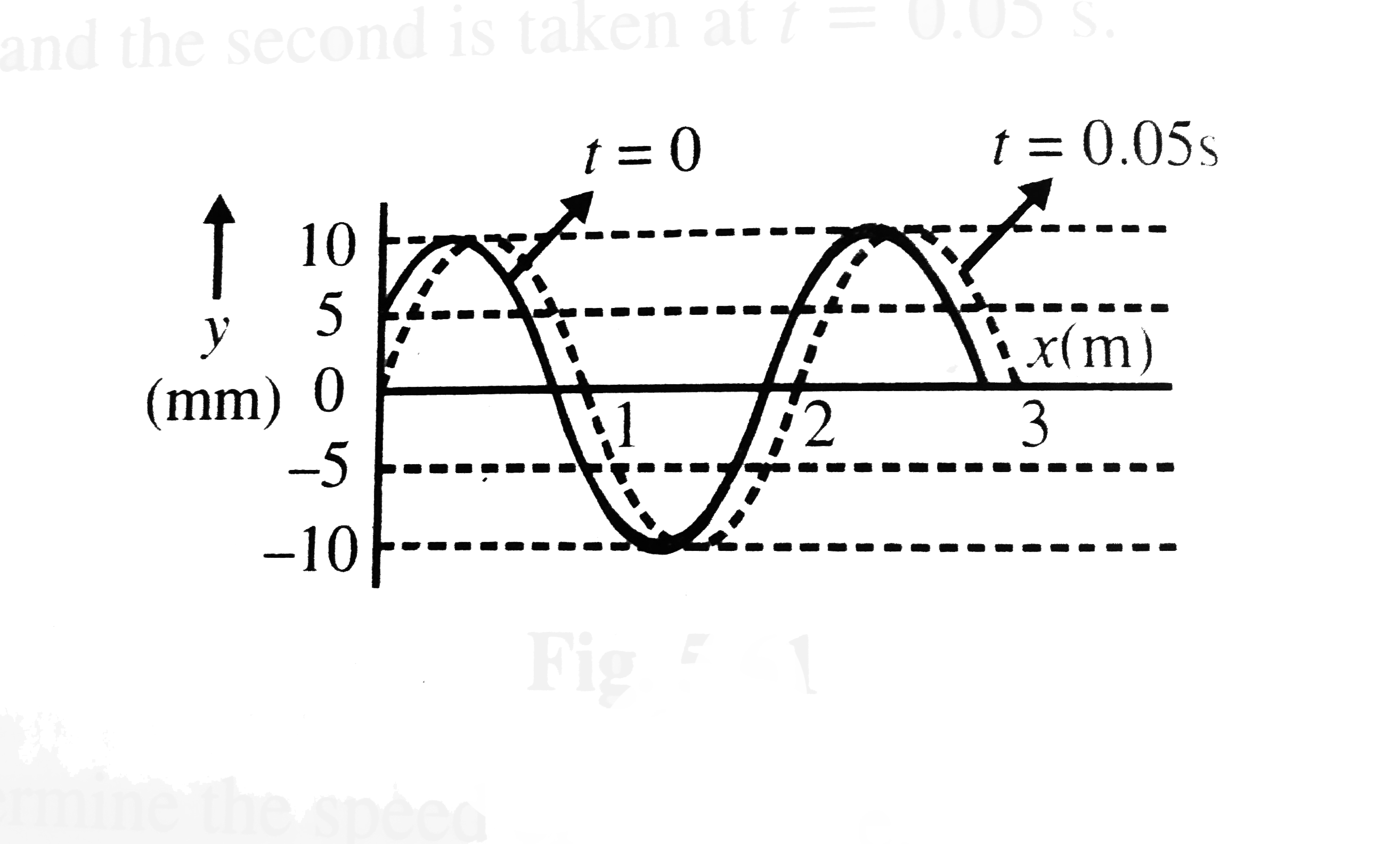
Determine the equation of the wave.
y10sin2πx−10/3πtπ/6
yπ10sinππx−π10/3ππtπππ/3ππ
yπ10sinππx−π10/3ππtπππ/6ππ
yπ10sinππx−π5/3ππtπππ/3ππ
The correct Answer is:c
The waves is travelling along the positivex-axis
∴y=Asin[kx−ωt+ϕ]
at x=0,y=Asin[−ωt+ϕ]
Also, at t=0,y=Asinϕ=A/2,
sinϕ=1/2
⇒ϕ=(π/6),(5π/6),…
and at t=0.05s,y=Asin(−ω20+ϕ)=0
or, −ω20+ϕ=0,π,2π,...
For t=0.05s and x=1m,
y=Asin(k−ω20+ϕ)=0
since, λ=2m
∴π−ω20+ϕ=0,π,2π,...
from Eqs. (i),(ii) and (ii), we get
ϕ=π/6
ϕ−ω20=0
ω=10π3
f=ω2π=53Hz
velocity of wave is
V=λf=(2)(5/3)=10/3m/s
Maximum velocity of the particle is
Vmax=oemgaA)10π/3))(10x10−3)=π/30m/s
Tension in the string is
T=μV2=(0.25)(10/3)2=25/9N.
the equation of the wave is
y=10sin[πx−(10/3)πt+(π/6)]
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning
6 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Two sine waves of same frequency and amplitude, travel on a stretched string in opposite directions. Speed of each wave is 10 cm/s. These two waves superimpose to form a standing wave pattern on the string. The maximum amplitude in the standing wave pattern is 0.5 mm. The figure shows the snapshot of the string at t = 0.Write the equation of the two travelling waves.

View SolutionShows a snapshot of a sinusoidal travelling wave taken at t=0.3s. The wavelength is 7.5 cm and amplitude is 2 cm. if the crest P was at x=0 at t=0, write the equation of travelling wave.
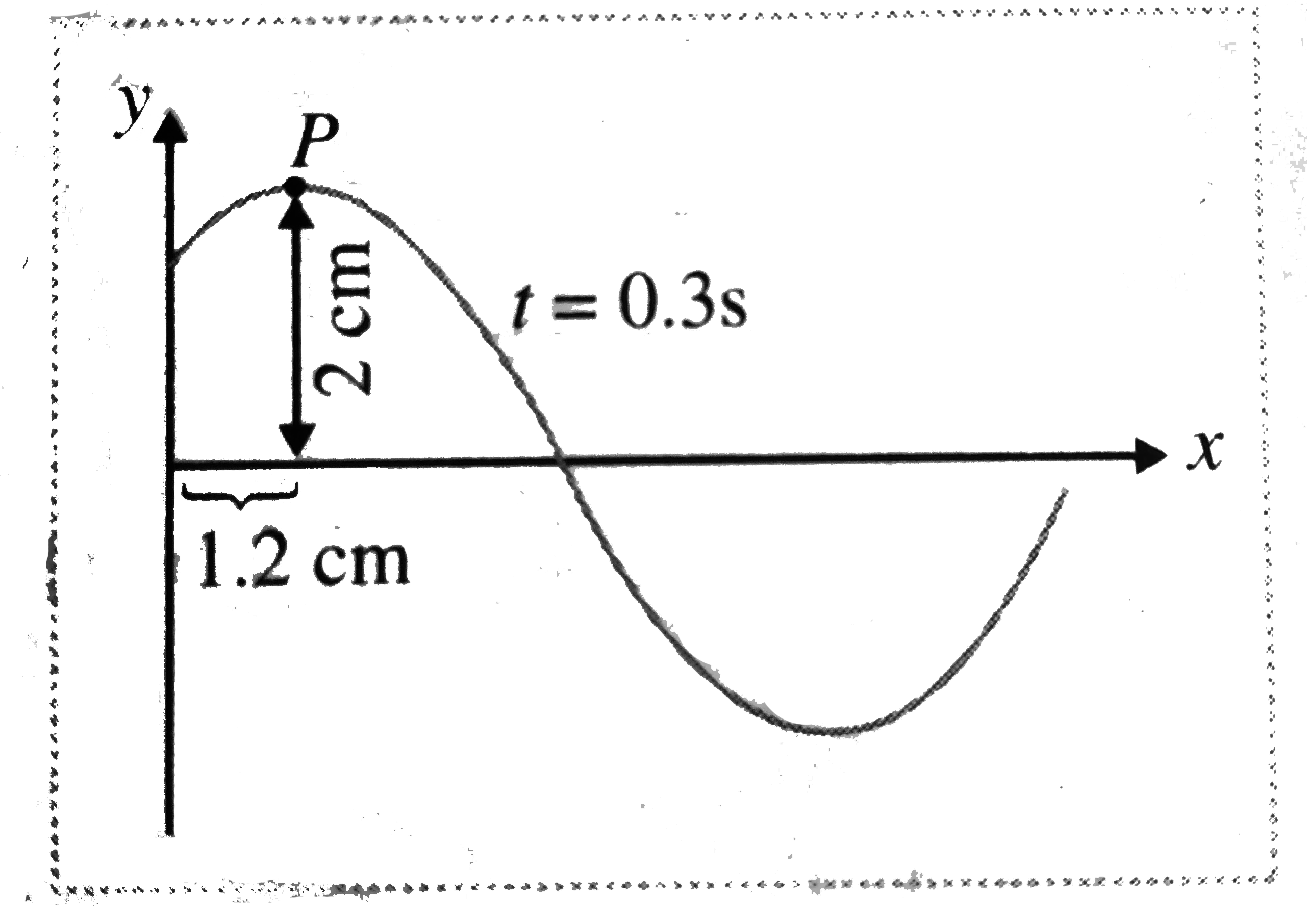
View Solution
Knowledge Check
The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
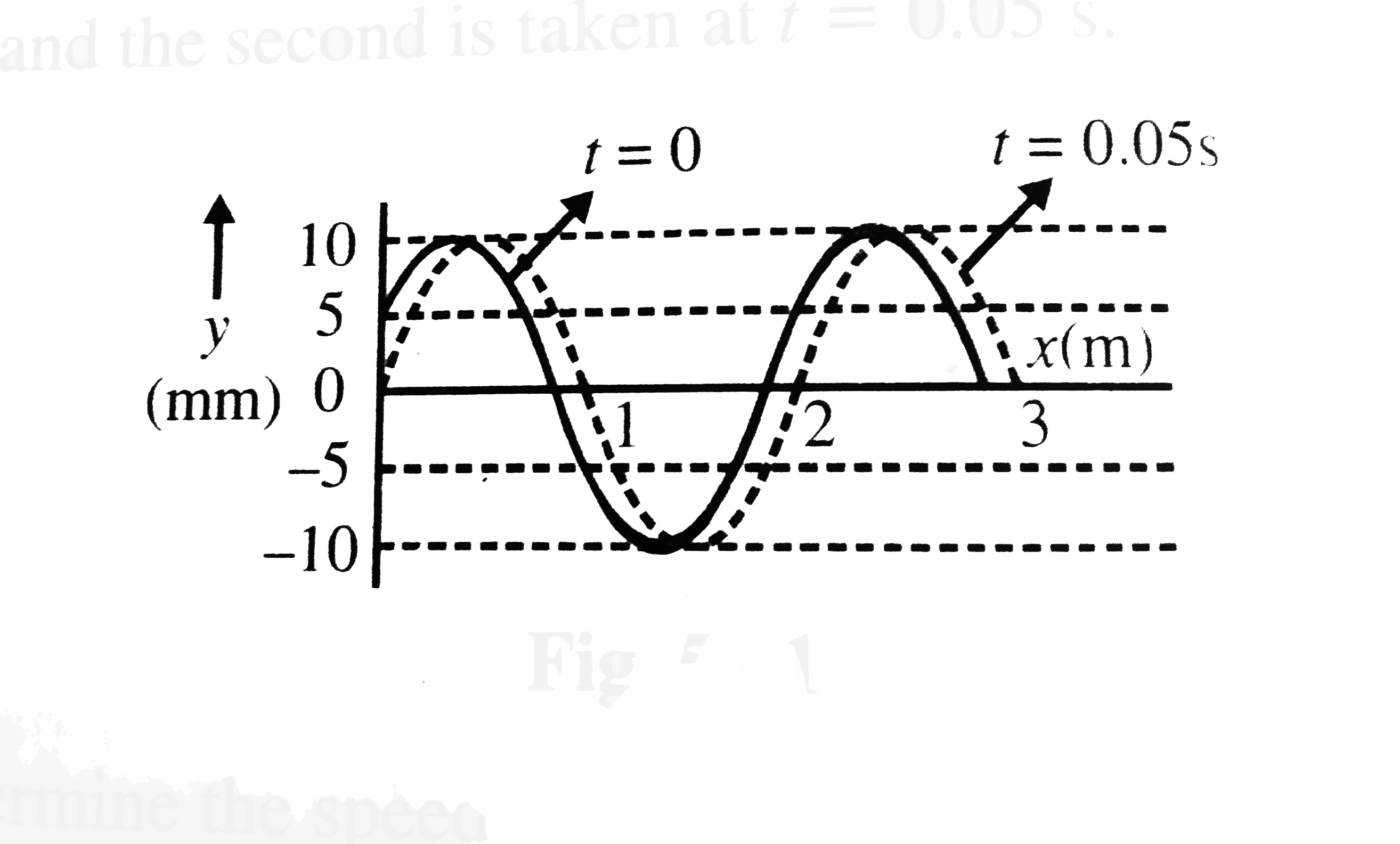
Determine the frequency of the wave.A5/3HzB10/3m/sC5HzD10HzThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
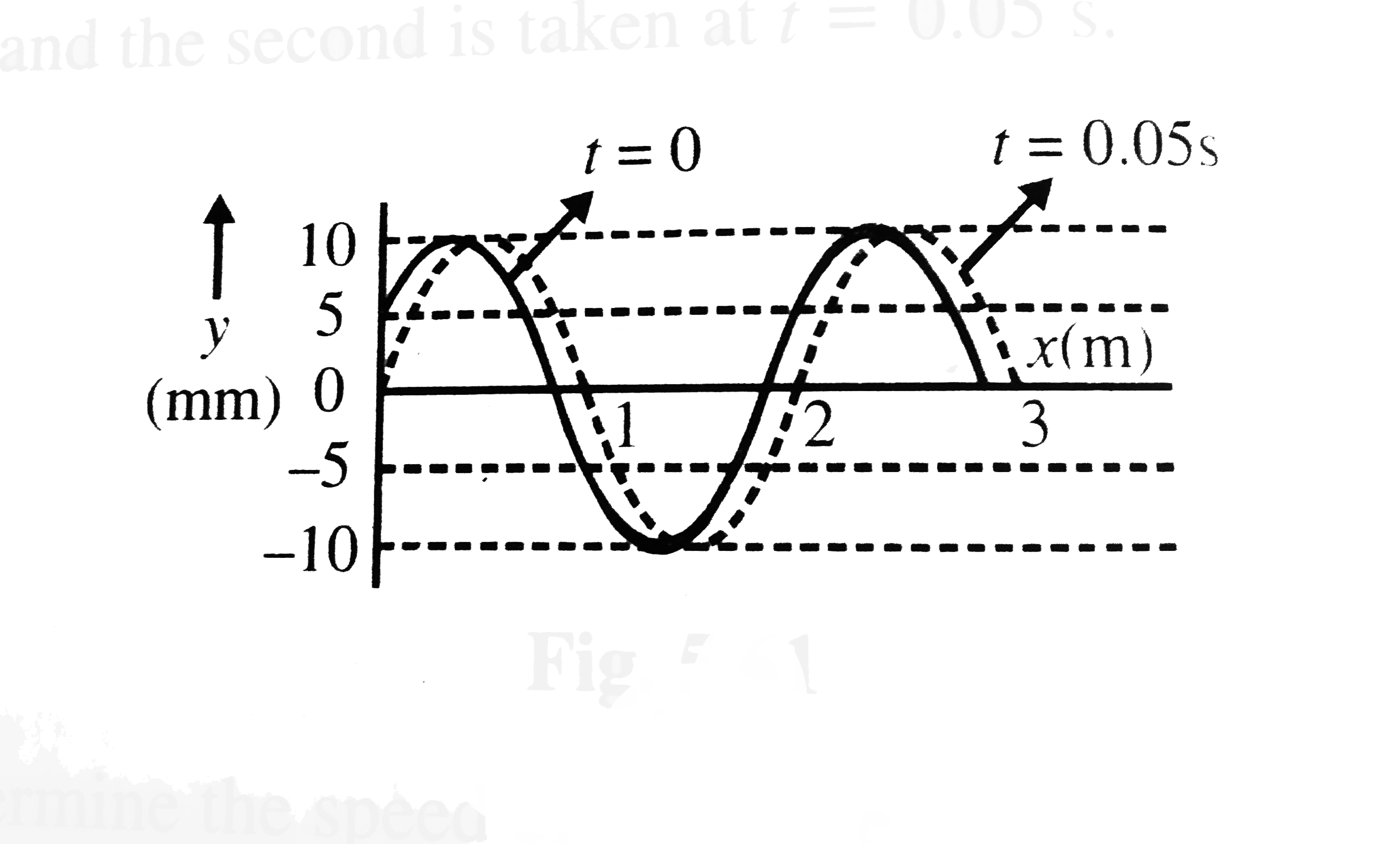
Determine the speed of the wave.A20/3m/sB10/3m/sC20m/sD10m/sThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
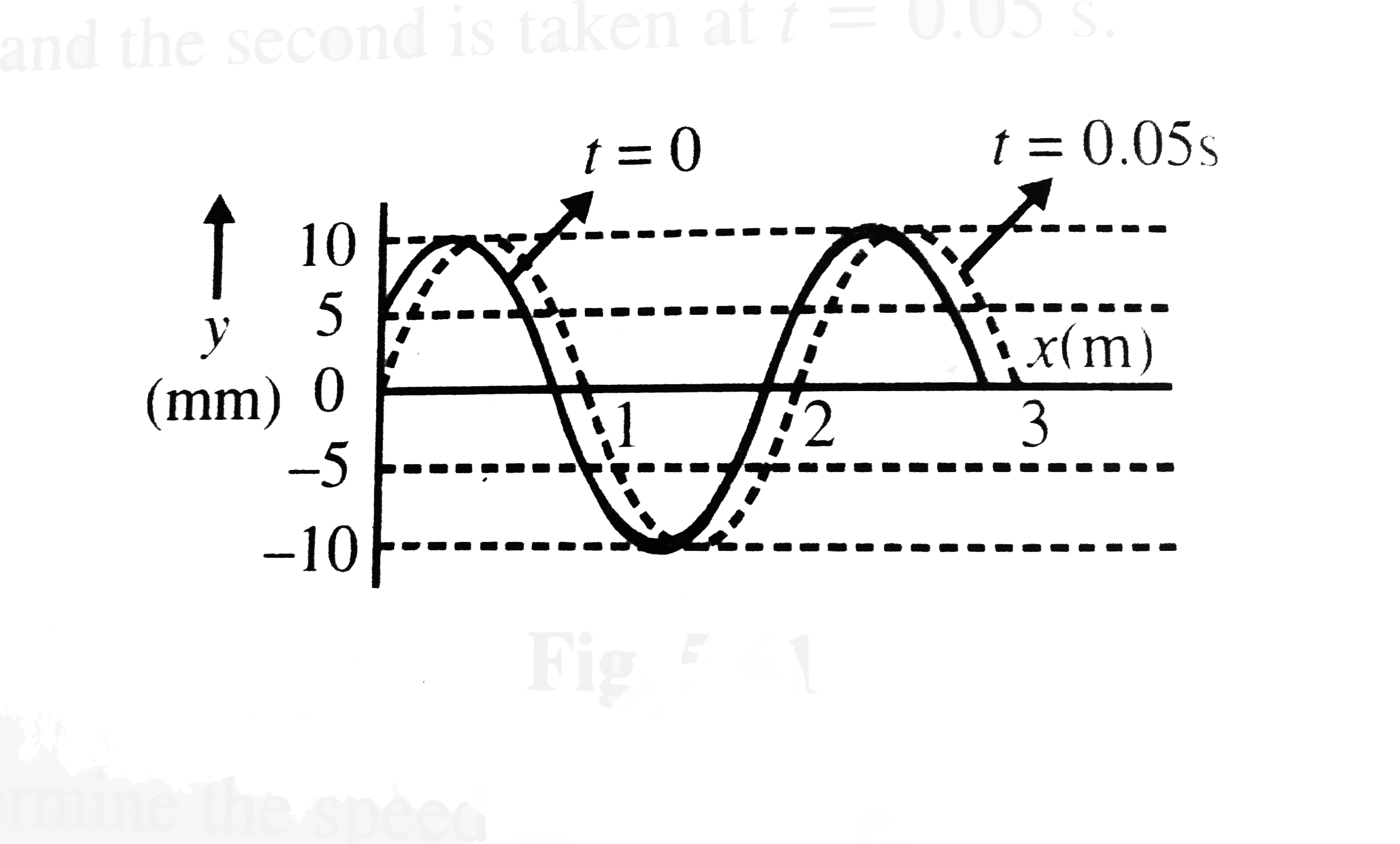
Determine the tension in the string.A25/3NB25/7NC5ND25/9N
A transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
View SolutionTwo strings A and B are connected together end to end as shown in the figure. The ratio of mass per unit length μBμA=4. The tension in the string is same. A travelling wave is coming from the string A towards string B. if the fraction of the power of the incident wave that goes in sting B is n9 the value of n is:

View SolutionThe equation of a trevelling wave In a uniform string of mass per unit length unit length μ is given as y=Asin(ω−kx).Find the total energy transferred through the origin in time interval from t = 0 to t=π/12ω.(You can use the formula in instantaneous power if you know)
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
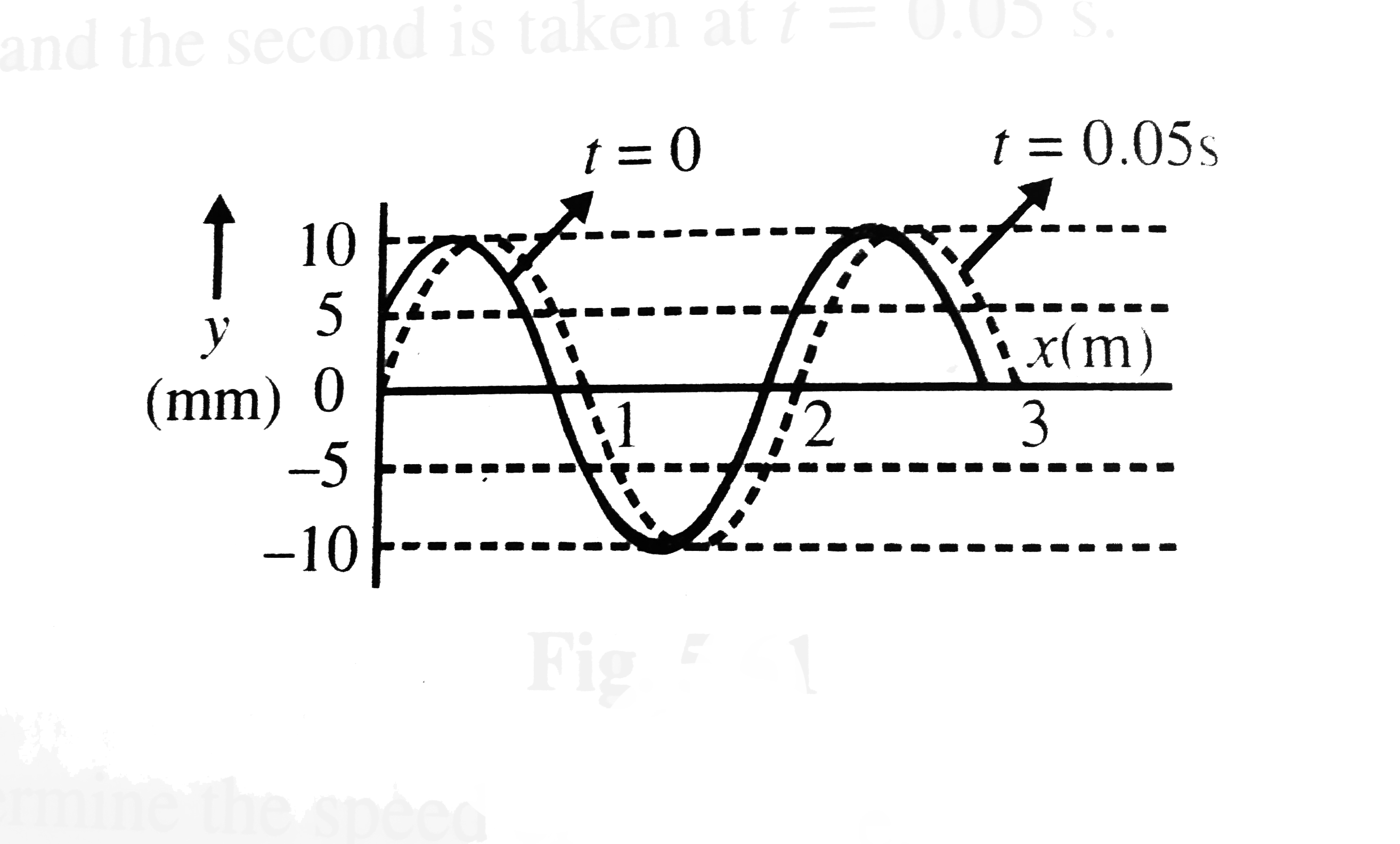
Determine the maximum speed of the particle.
View SolutionA string consists of two parts attached at x=0 , The right part of the string (x<0) has mass per unit length μr and the left part of the string (x<0) has mass per unit length μl The tension in the string is T. If a wave of units amplitude travels along the left part of the string,what is the amplitude of the wave that is transmitted to the right part of the string?
View Solution
