The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
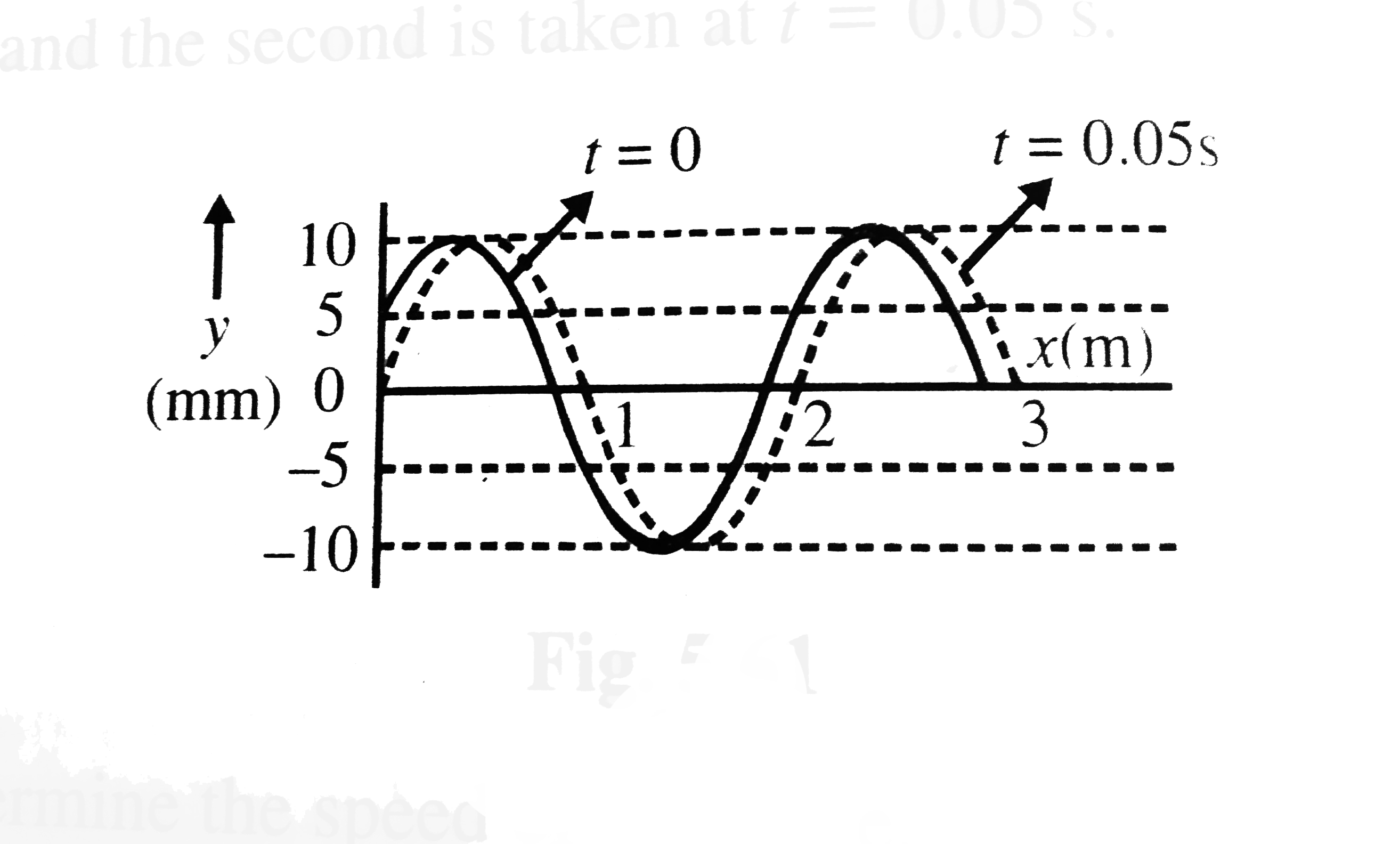
Determine the frequency of the wave.
5/3Hz
10/3m/s
5Hz
10Hz
The correct Answer is:a
The waves is travelling along the positivex-axis
∴y=Asin[kx−ωt+ϕ]
at x=0,y=Asin[−ωt+ϕ]
Also, at t=0,y=Asinϕ=A/2,
sinϕ=1/2
⇒ϕ=(π/6),(5π/6),…
and at t=0.05s,y=Asin(−ω20+ϕ)=0
or, −ω20+ϕ=0,π,2π,...
For t=0.05s and x=1m,
y=Asin(k−ω20+ϕ)=0
since, λ=2m
∴π−ω20+ϕ=0,π,2π,...
from Eqs. (i),(ii) and (ii), we get
ϕ=π/6
ϕ−ω20=0
ω=10π3
f=ω2π=53Hz
velocity of wave is
V=λf=(2)(5/3)=10/3m/s
Maximum velocity of the particle is
Vmax=oemgaA)10π/3))(10x10−3)=π/30m/s
Tension in the string is
T=μV2=(0.25)(10/3)2=25/9N.
the equation of the wave is
y=10sin[πx−(10/3)πt+(π/6)]
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning
6 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Two sine waves of same frequency and amplitude, travel on a stretched string in opposite directions. Speed of each wave is 10 cm/s. These two waves superimpose to form a standing wave pattern on the string. The maximum amplitude in the standing wave pattern is 0.5 mm. The figure shows the snapshot of the string at t = 0.Write the equation of the two travelling waves.

View SolutionTwo strings A and B are connected together end to end as shown in the figure. The ratio of mass per unit length μBμA=4. The tension in the string is same. A travelling wave is coming from the string A towards string B. if the fraction of the power of the incident wave that goes in sting B is n9 the value of n is:

View Solution
Knowledge Check
The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
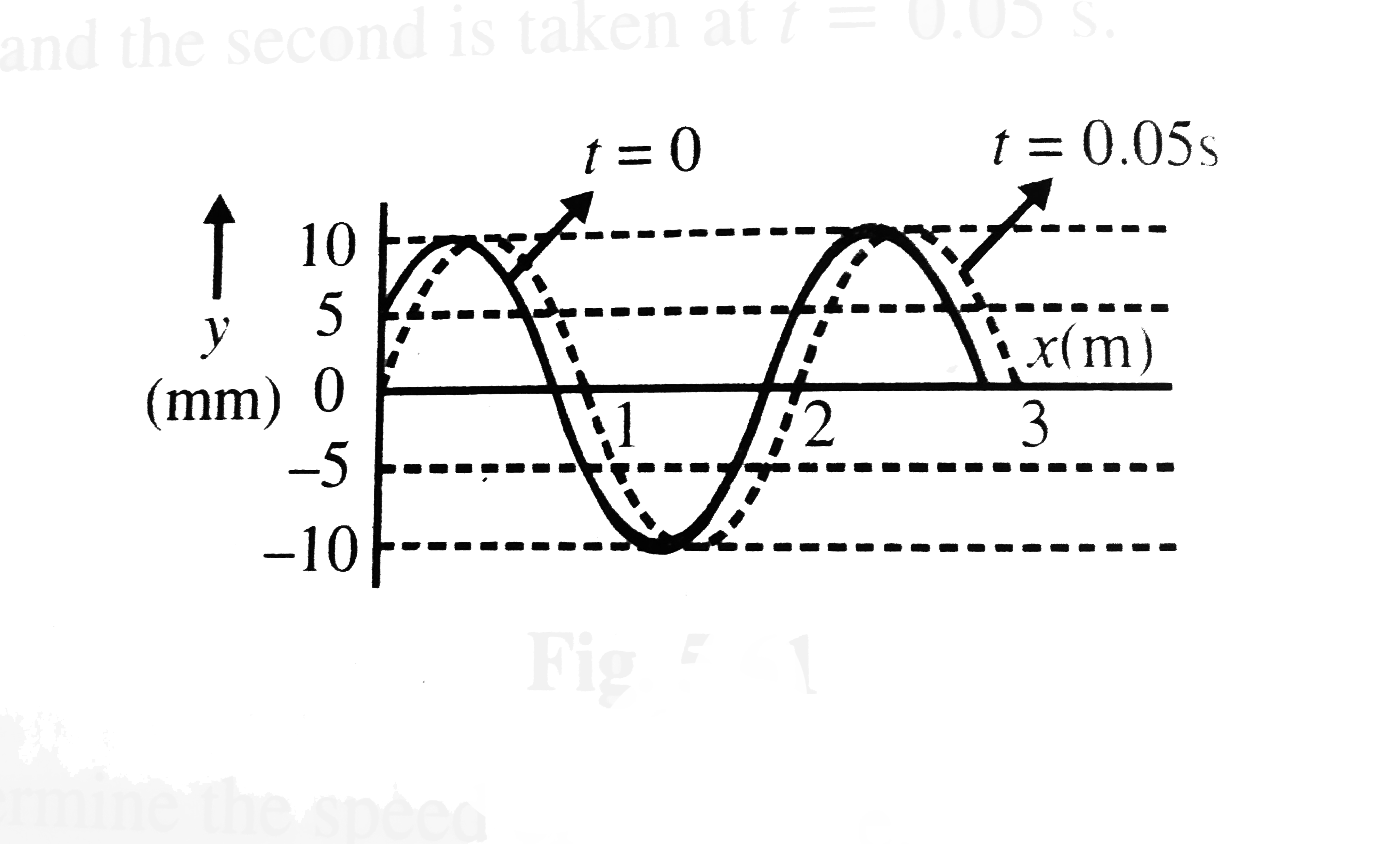
Determine the equation of the wave.Ay10sin2πx−10/3πtπ/6Byπ10sinππx−π10/3ππtπππ/3ππCyπ10sinππx−π10/3ππtπππ/6ππDyπ10sinππx−π5/3ππtπππ/3ππThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
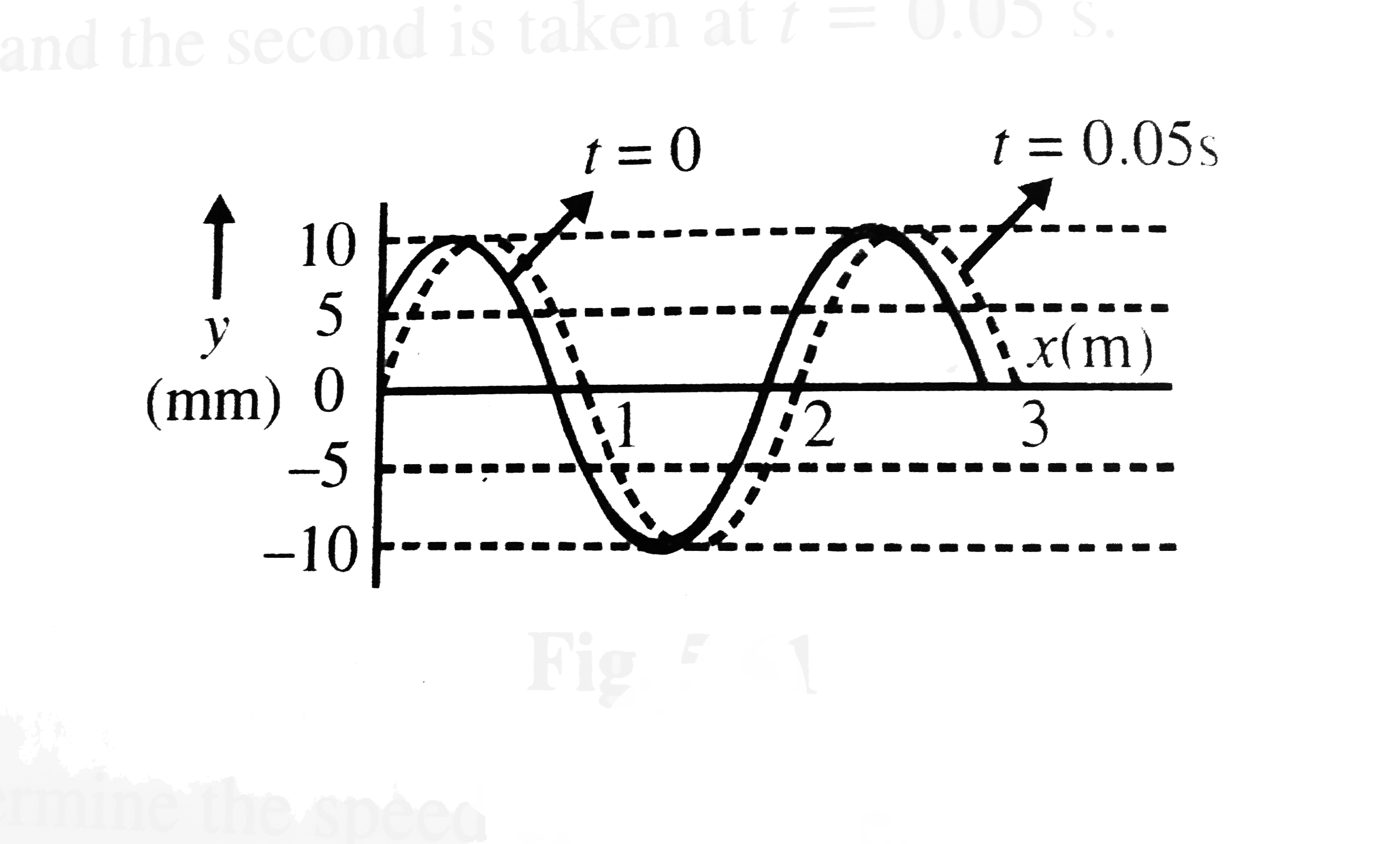
Determine the speed of the wave.A20/3m/sB10/3m/sC20m/sD10m/sThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.

Determine the tension in the string.A25/3NB25/7NC5ND25/9N
A wave travelling along a string is given by y(x,t)=20sin2π(t−0.003x) x, y are in cm and t is in seconds.
Find the amplitude, frequency, wavelength and velocity of the wave.
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
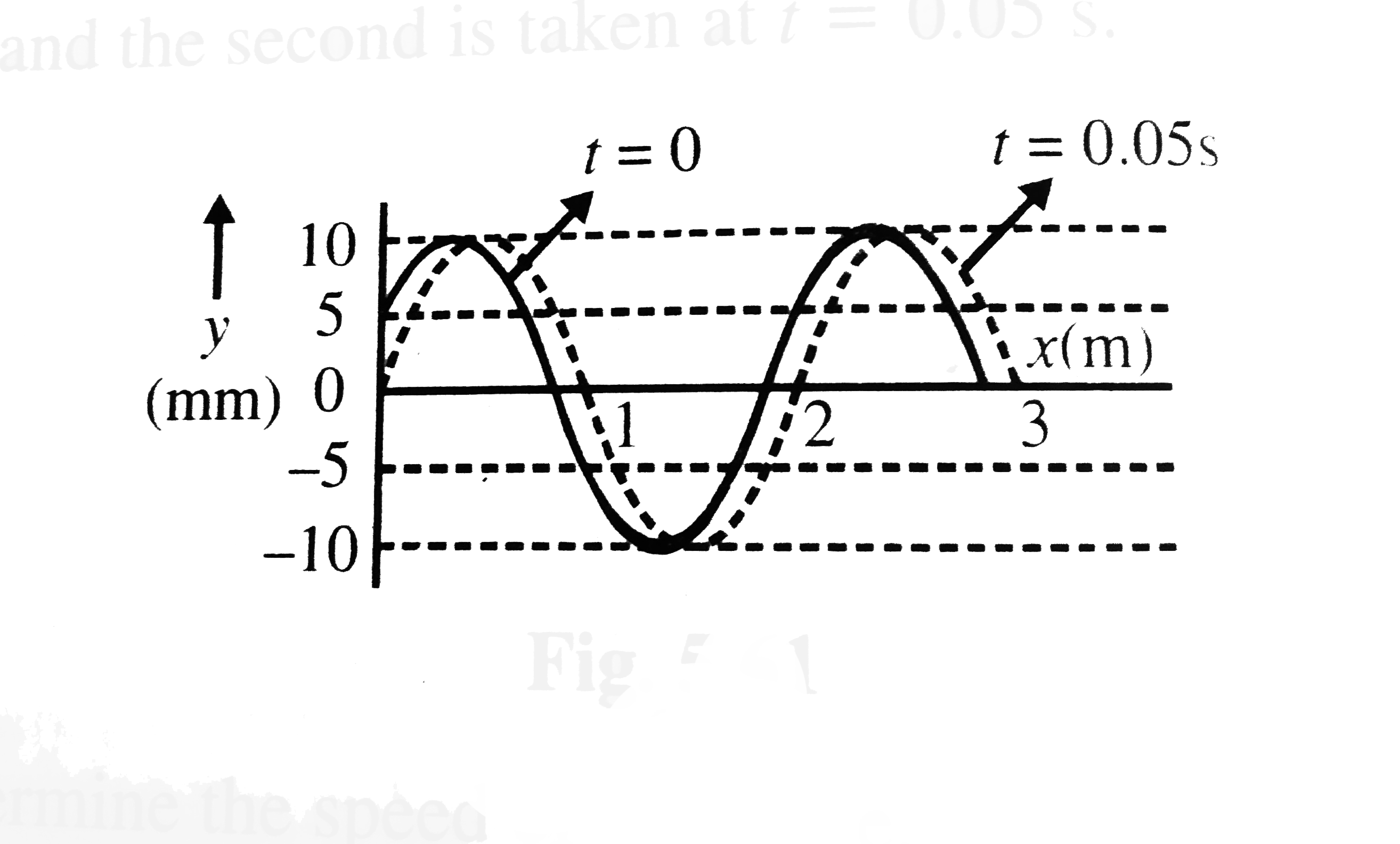
Determine the maximum speed of the particle.
View SolutionFrom a wave equation
y=0.5sin(2π3.2)(64t−x).
the frequency of the wave is
View SolutionA string consists of two parts attached at x=0 , The right part of the string (x<0) has mass per unit length μr and the left part of the string (x<0) has mass per unit length μl The tension in the string is T. If a wave of units amplitude travels along the left part of the string,what is the amplitude of the wave that is transmitted to the right part of the string?
View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,
View Solution
