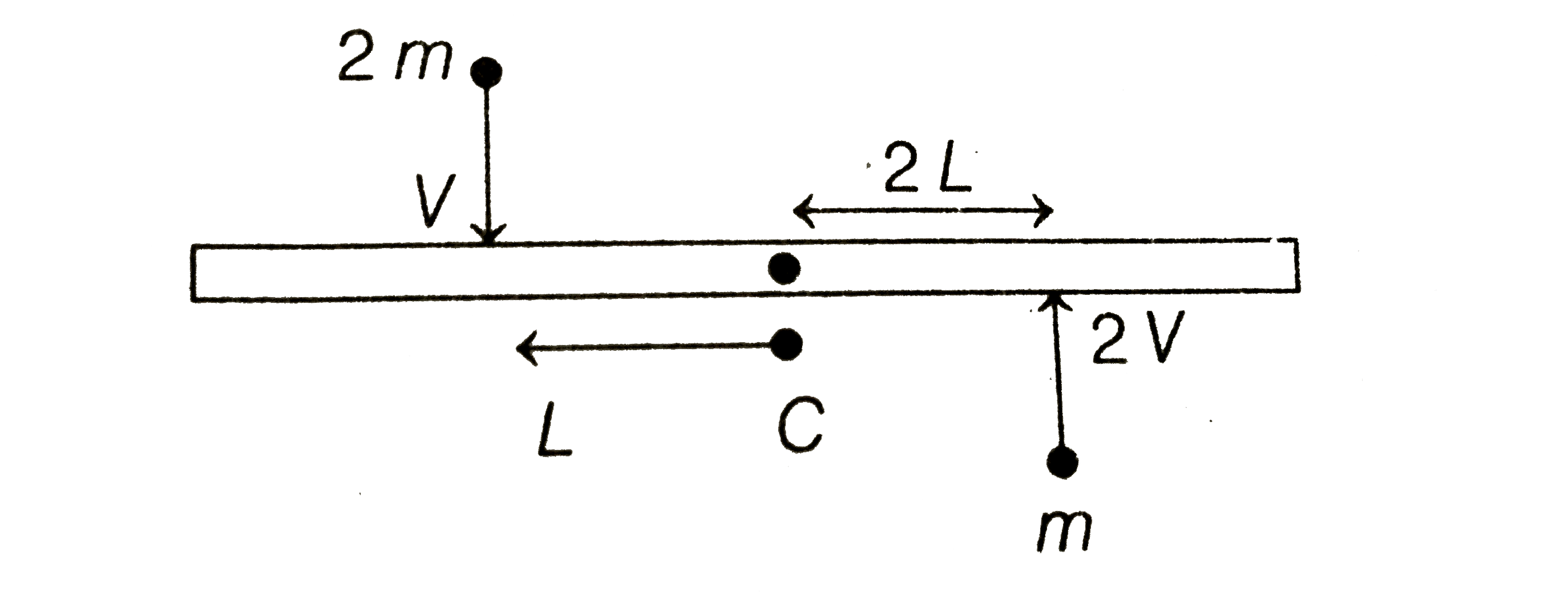
A uniform rod of length '6L' and mass '8 m' is pivoted at its centre 'C'. Two masses 'm' and '2m' with speed 2v, v as shown strikes the rod and stick to the rod. Initially the rod is at rest. Due to impact, if it rotates with angular velocity $' ω'$ then $' ω'$ will be

$\frac{v}{5 L}$

zero

$\frac{8 v}{6 L}$

$\frac{11 v}{3 L}$

Text Solution

Verified by Experts

The correct Answer is:A

A rod of length 6L and mass 8m is given in figure,

When two masses strike the rod, then angular momentum imparted to rod,
$L_{1} + L_{2} = 2 m v (L) + m (2 v) (2 L)$
= 6mvL
Now, after striking of masses to rod the angular momentum of comP,lete rod about the centre C,
$L_{r o d} I ω$
where, $ω$ = angular velocity of the rod
and I = moment of inertia of the rod.
The moment of inertia of rod
$I = \frac{M l^{2}}{12} = \frac{8 m {(6 L)}^{2}}{12} = 24 m L^{2}$
$∴$ M = 8m andl= 6L (given)
Now, moment of inertia of two masses after the striking to l rod,
$I = 2 m {(L)}^{2} = 2 m L^{2}$
and $I_{2} = m {(2 L)}^{2} = 4 m L^{2}$
$∴$ The net moment of the inertia about the centre of rod,
$I = 24 m L^{2} + 2 m L^{2} + 4 m L^{2}$
$! I = 30 m L^{2}$
By putting this value in Eq. (i), we get
$L_{r o d} = 30 M L^{2} ω$
From the law of conservation of angular momentum,
$L_{1} + L_{2} = L_{rod}$
$! 6 m v L = 30 m L^{2} ω$
$! ω = \frac{v}{5 L}$
Hence, the anguler velocity of the rod is $\frac{v}{5 L}$

Updated on:21/07/2023

Class 12 PHYSICS MHTCET 2019 PAPER 1

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A uniform rod of length $L$ lies on a smooth horizontal table. The rod has a mass $M$ . A particle of mass $m$ moving with speed $v$ strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass $C$ and the angular, velocity of the system about the centre of mass after the collision.
A $\frac{2 m v}{M + m}, \frac{3 M v}{(M + 2 m) L}$
B $\frac{M v}{M + m}, \frac{6 M v}{(M + 4 m) L}$
C $\frac{2 m v}{M + m}, \frac{3 M v}{(M + 4 m) L}$
D $\frac{m v}{M + m}, \frac{6 M v}{(M + 4 m) L}$
Question 2 - Select One
A uniform rod of length $L$ lies on a smooth horizontal table. The rod has a mass $M$ . A particle of mass $m$ moving with speed $v$ strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass $C$ of the system constituting 'the rod plus the particle'.
A $\frac{2 M v}{M - m}$
B $\frac{2 m v}{M + m}$
C $\frac{M v}{M + m}$
D $\frac{m v}{M + m}$
Question 3 - Select One
A uniform rod of length $L$ lies on a smooth horizontal table. The rod has a mass $M$ . A particle of mass $m$ moving with speed $v$ strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the angular momentum of the particle and of then about the centre of mass $C$ before the collision.
A $\frac{M^{2} m v l}{4 {(M + m)}^{2}}, \frac{m^{2} M v l}{4 (m + M)}$
B $\frac{M^{2} m v l}{2 {(M + m)}^{2}}, \frac{M^{2} M v l}{2 (m + M)}$
C $\frac{M^{2} m v l}{{(M + m)}^{2}}, \frac{m^{2} M v l}{(m + M)}$
D $\frac{2 M^{2} m v l}{{(M + m)}^{2}}, 2 \frac{m^{2} M v l}{(m + M)}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-MHTCET 2019 PAPER 1-PHYSICS

Home
Ask Doubt
Profile

A uniform rod of length '6L' and mass '8 m' is pivoted at its centre 'C'. Two masses 'm' and '2m' with speed 2v, v as shown strikes the rod and stick to the rod. Initially the rod is at rest. Due to impact, if it rotates with angular velocity 'ω' then 'ω' will be

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-MHTCET 2019 PAPER 1-PHYSICS

A uniform rod of length '6L' and mass '8 m' is pivoted at its centre 'C'. Two masses 'm' and '2m' with speed 2v, v as shown strikes the rod and stick to the rod. Initially the rod is at rest. Due to impact, if it rotates with angular velocity $' ω'$ then $' ω'$ will be