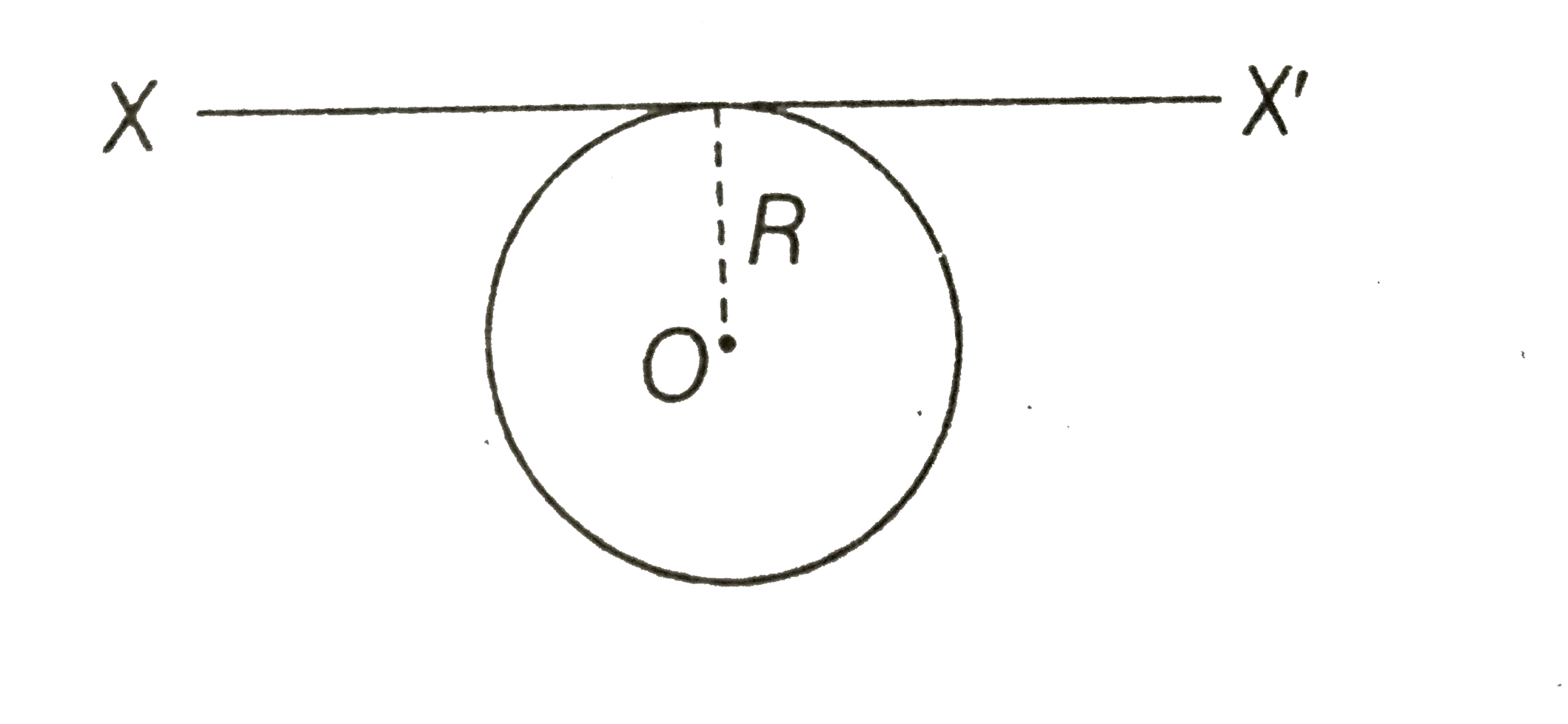
A thin metal wire of length 'L' and uniform linear mass density 'p' is bent into a circular coil with 'O' as centre. The moment of inertia of a coil about the axis XX' is
3pL38π2
pL34π2
3pL34π2
pL38π2
The correct Answer is:A
Moment of inertia of a thin circular coil
I=MR22
Now moment of inertia of a ring about axis XX' as in figure below,

IXX'=MR22+MR2=32MR2 ..(i)
(Using theorem of parallel axis)
Given, L = length of wire of ring
and p = linear mass density
Then, mass of the ring = linear density × length
!M=pL
and L=2πR
!R=L2π ...(iii)
Now, putting the value from Eqs. (ii) and (iii) in (i), we get
IXX'=32(pL)L24π2!3pL38π2
Hence, option a is correct.
Topper's Solved these Questions
Similar Questions
A thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
View SolutionA uniform wire of length l and mass M is bent in the shape of a semicircle of radius r as shown in figure. Calculate moment of intertia about the axis XX'
View Solution
Knowledge Check
A thin wire of length L and uniform linear mass density p is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
 ApL38π2BpL316π2C5pL316π2D3pL38π2
ApL38π2BpL316π2C5pL316π2D3pL38π2A thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is :
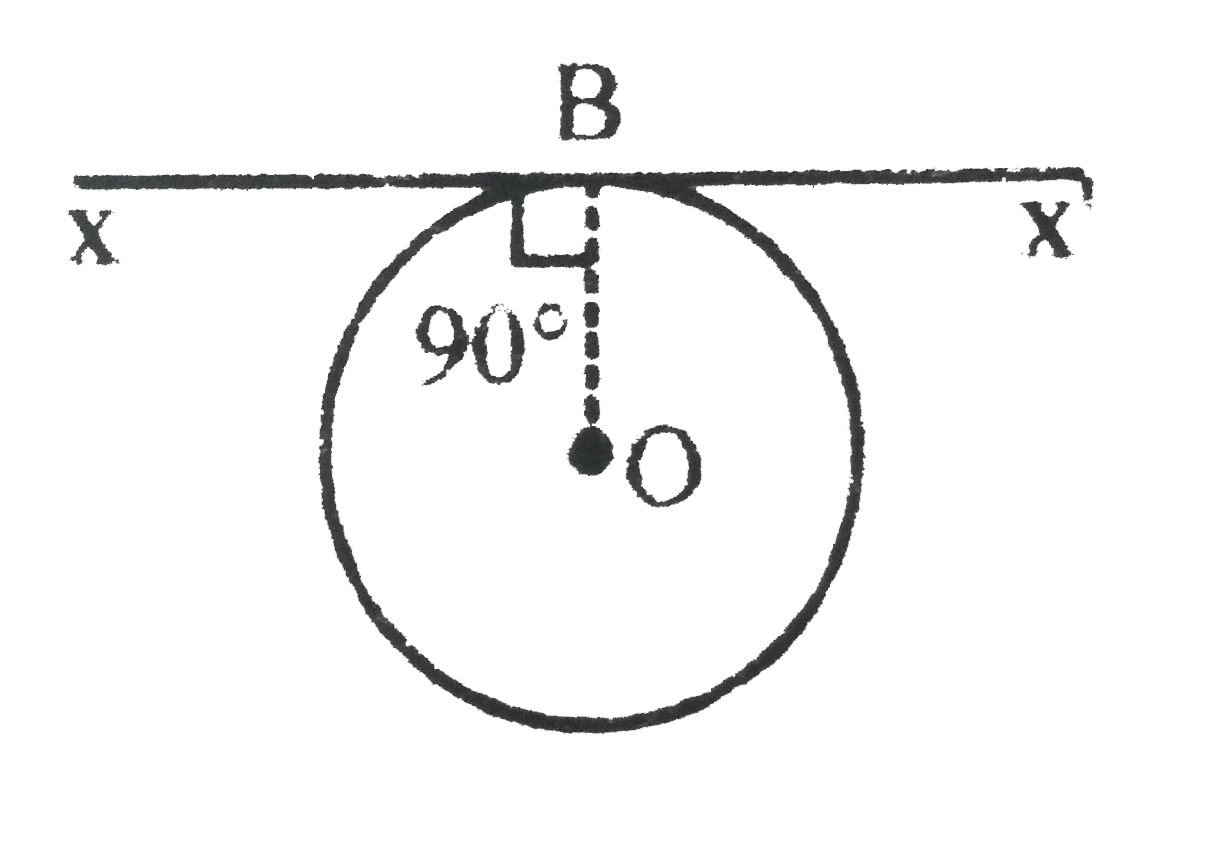 .AρL38π2BρL316π2C5ρL316π2D3ρL38π2
.AρL38π2BρL316π2C5ρL316π2D3ρL38π2A thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is :
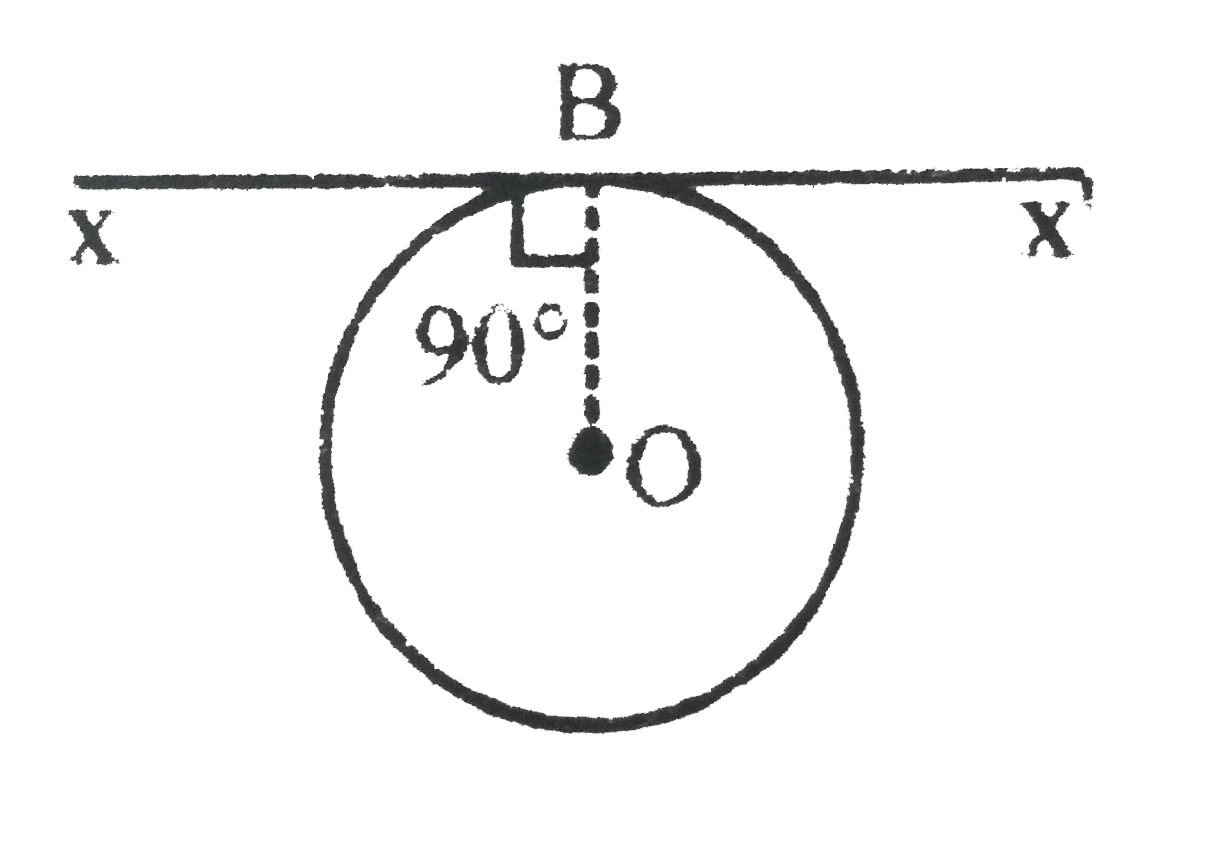 .AρL3/8π2BρL3/16π2C5ρL3/16π2D3ρL3/8π2.
.AρL3/8π2BρL3/16π2C5ρL3/16π2D3ρL3/8π2.
A thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is A cubical block of side L rests on a rough horizontal surface with coefficient of friction sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
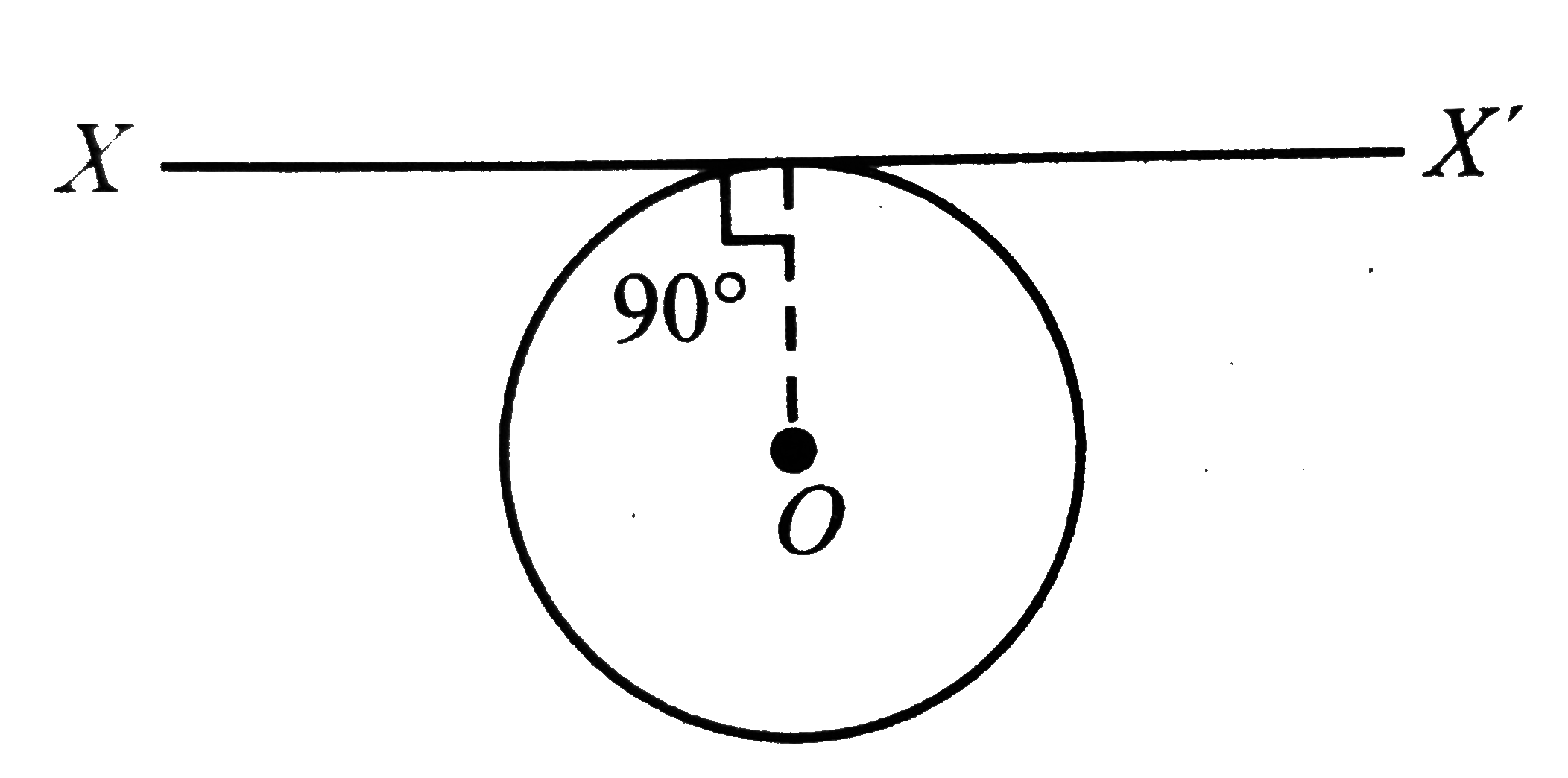
View SolutionA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown in the figure. What is the moment of inertia of the loop anout the axis XX'?
View SolutionA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is :
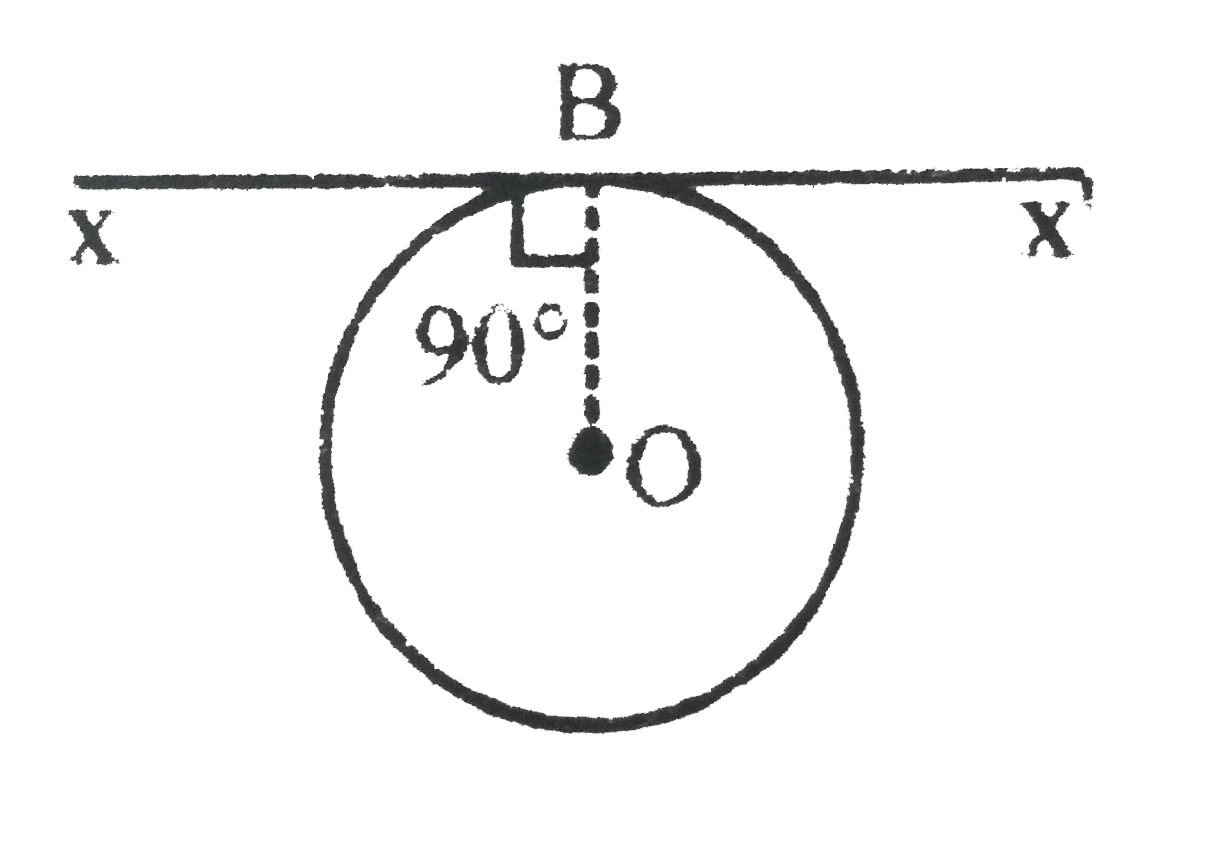 .
.
View SolutionA wire of mass 'm' and length 'l' is bent in the form of a circular ring. The moment of inertia of the ring about its axis is-
View SolutionA wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
View Solution
