Find the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
Baxis=μ04π.nAIr3
Baxis=μ04π.2nIAr3
Baxis=μ04π.2nIAr3
Baxis=μ04π.nIAr3
The correct Answer is:B
As we know that the magnetic field on the axis of a circular current carrying loop,
B=μ0nla22(r2+a2)3/2 ….(i)
where , I = current through the coil , a = radius of a circular loop, r = distance of point from the centre along the axis and n = number of turns in the coil.
Area of the coil , A= πa2
!a2=Aπ ...( ii)
and it r>>a then, (r2+a2)3/2≈r3 ...(iii)
From Eqs. (i), (ii) and (iii), we get
B=(μ0nl2r3)Aπ×22
!B=2μ0nlA4πr3
So, option (b) is correct.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic field at the centre of current carrying coil is
Aμ0ni2rBμ02πnirCμ0ni4rDμ0niThe magnetic moment of a circular coil carrying current is
ADirectly proportional to the length of the wire in the coilBInversely proportional to the length of the wire in the coilCDirectly proportional to the square of the length of the wire in the coilDInversely proportional to the square of the length of the wire in the coilA flat circular coil, carrying a current, has a magnetic moment μ
Aμ has only magnitude, it does not have directionBThe direction of μ is along the normal to the plane of the coilCThe direction of μ depends on the direction of the current flowDThe direction of μ does not change if the current in the coil is reversed
Magnetic field induction at the centre of a circular coil shown in the figure is
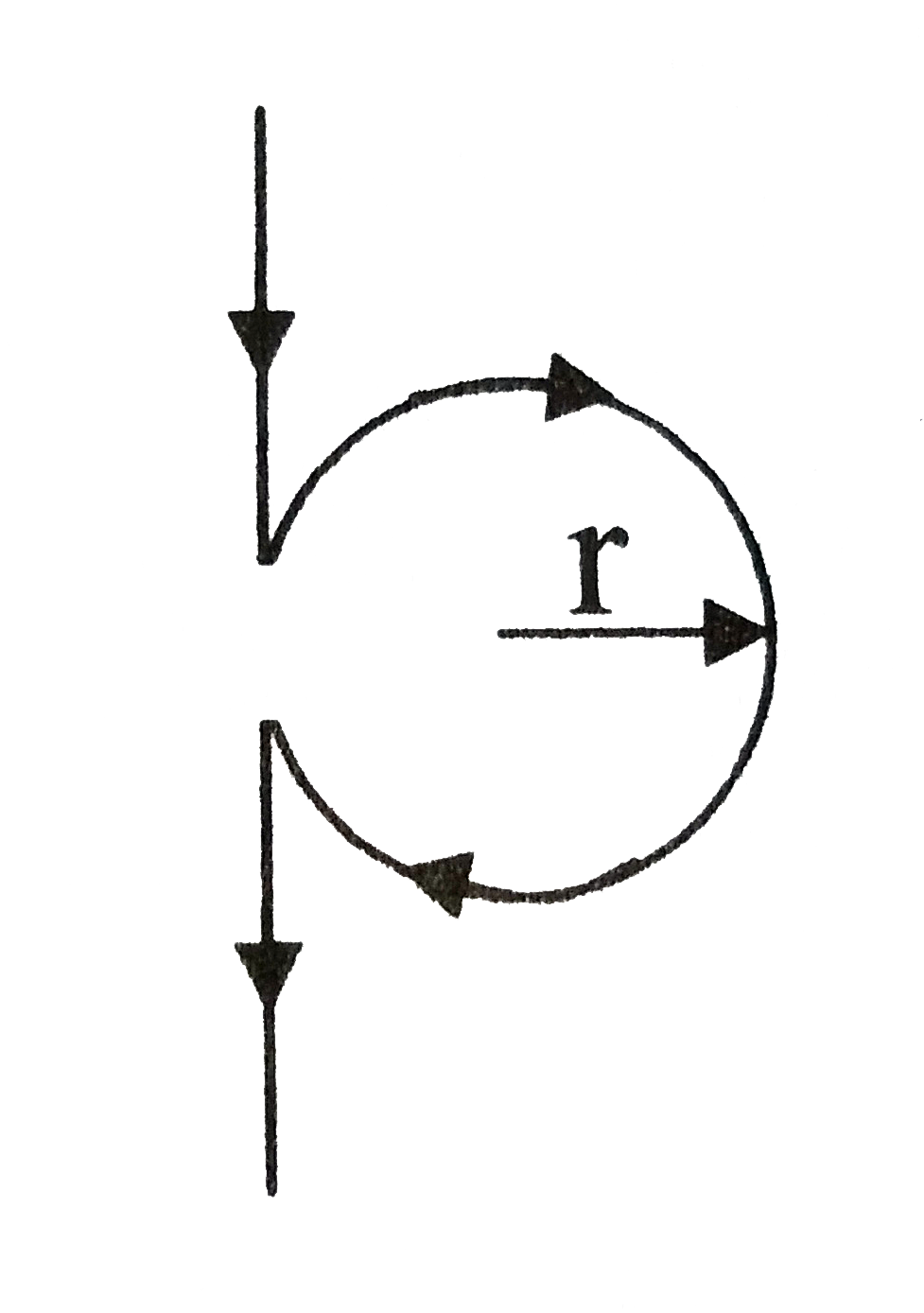
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUsing Biot - Savart's law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is

View SolutionThe magnetic induction at a point on the axis of a circular current carrying coil at a distance equal to the radius of coil carrying a current of 0.5 A is
View Solution
