A body is thrown vertically upwards. If air resistance is to be taken into account, then the time during which the body rises is.
Equal to the time of fall
Less than the time of fall
Greater than the time of fall
Twice the time of fall
The correct Answer is:B
To solve the problem of a body thrown vertically upwards considering air resistance, we can follow these steps:
Step 1: Understand the Forces Acting on the Body
When a body is thrown upwards, two forces act on it:
1. The gravitational force (downward) which is equal to mg.
2. The air resistance (also downward) which we will denote as Fa and is assumed to be constant for this problem.
Step 2: Write the Equation of Motion
The net force acting on the body when it is moving upwards is:
Fnet=−mg−Fa
This gives us the acceleration a of the body as:
a=−g−a
where a is the magnitude of air resistance per unit mass.
Step 3: Use Kinematic Equations
The initial velocity of the body is u, and we want to find the time t1 taken to reach the maximum height where the final velocity v=0. Using the equation:
v=u+at
At maximum height, v=0:
0=u−(g+a)t1
Rearranging gives:
t1=ug+a
Step 4: Analyze the Time of Fall
When the body falls back down, the forces acting on it are:
1. Gravitational force (downward) mg.
2. Air resistance (upward) Fa.
The net acceleration during the fall is:
afall=g−a
The initial velocity for the fall is 0 (at the maximum height). We can use the same kinematic equation:
h=ut+12afallt22
Since u=0 for the fall, we have:
h=12(g−a)t22
Step 5: Calculate the Height
From the upward motion, we can find the height h:
h=u22(g+a)
Step 6: Set the Heights Equal
Since the height reached during the rise is equal to the height fallen, we can set the two height equations equal:
u22(g+a)=12(g−a)t22
Cancelling 12 gives:
u2g+a=(g−a)t22
Step 7: Solve for t2
Rearranging gives:
t22=u2(g+a)(g−a)
Taking the square root:
t2=u√(g+a)(g−a)
Step 8: Compare t1 and t2
Now we have:
- Time of rise: t1=ug+a
- Time of fall: t2=u√(g+a)(g−a)
To compare t1 and t2, we can analyze the ratios:
t2t1=(g+a)√(g+a)(g−a)
Since g+a>g−a, it follows that t2>t1.
Conclusion
Thus, the time during which the body rises t1 is less than the time during which it falls t2.
When a body is thrown upwards, two forces act on it:
1. The gravitational force (downward) which is equal to mg.
2. The air resistance (also downward) which we will denote as Fa and is assumed to be constant for this problem.
The net force acting on the body when it is moving upwards is:
Fnet=−mg−Fa
This gives us the acceleration a of the body as:
a=−g−a
where a is the magnitude of air resistance per unit mass.
The initial velocity of the body is u, and we want to find the time t1 taken to reach the maximum height where the final velocity v=0. Using the equation:
v=u+at
At maximum height, v=0:
0=u−(g+a)t1
Rearranging gives:
t1=ug+a
When the body falls back down, the forces acting on it are:
1. Gravitational force (downward) mg.
2. Air resistance (upward) Fa.
afall=g−a
The initial velocity for the fall is 0 (at the maximum height). We can use the same kinematic equation:
h=ut+12afallt22
Since u=0 for the fall, we have:
h=12(g−a)t22
From the upward motion, we can find the height h:
h=u22(g+a)
Since the height reached during the rise is equal to the height fallen, we can set the two height equations equal:
u22(g+a)=12(g−a)t22
Cancelling 12 gives:
u2g+a=(g−a)t22
Rearranging gives:
t22=u2(g+a)(g−a)
Taking the square root:
t2=u√(g+a)(g−a)
Now we have:
- Time of rise: t1=ug+a
- Time of fall: t2=u√(g+a)(g−a)
t2t1=(g+a)√(g+a)(g−a)
Since g+a>g−a, it follows that t2>t1.
Thus, the time during which the body rises t1 is less than the time during which it falls t2.
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:AIIMS Questions
Explore 20 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Chapter Test
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
(a) A ball is thrown vertically upward with speed 10m/s and it returns to the ground with speed 8m/s. Find the maximum height attained by the ball.
(b) A ball is thrown vertically upward and if air resistance is half of weight of the ball, find the ratio of time of ascent and time of descent.
(C) Two balls A and B(mA=2mB=2m) are thrown vertically upward. If air resistance is mg/2, find ratio of maximum height attained by them.
View SolutionA body is thrown vertically upwards which graph represents variation of velocity w.r.t time
View Solution
Knowledge Check
A ball is thrown vertically upwards .Assuming the air resistance to be constant and considerable :
Athe time of ascent < the time of descentBthe time of ascent the tine of descentCthe time of ascent = the time of descentDthe time of ascent > the time of descentA body is thrown vertically upwards and rises to a height of 10m. The velocity with which the body was thrown is (g - 9.8m/(s2)
A10m/sB20m/sC14m/sDnone of theseA body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A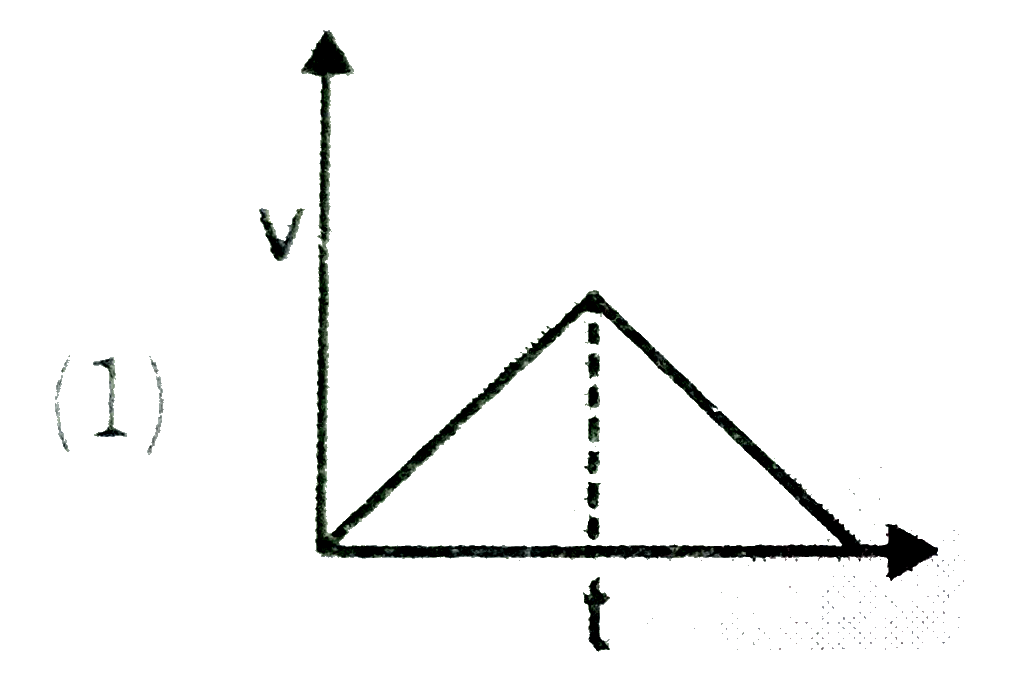 B
B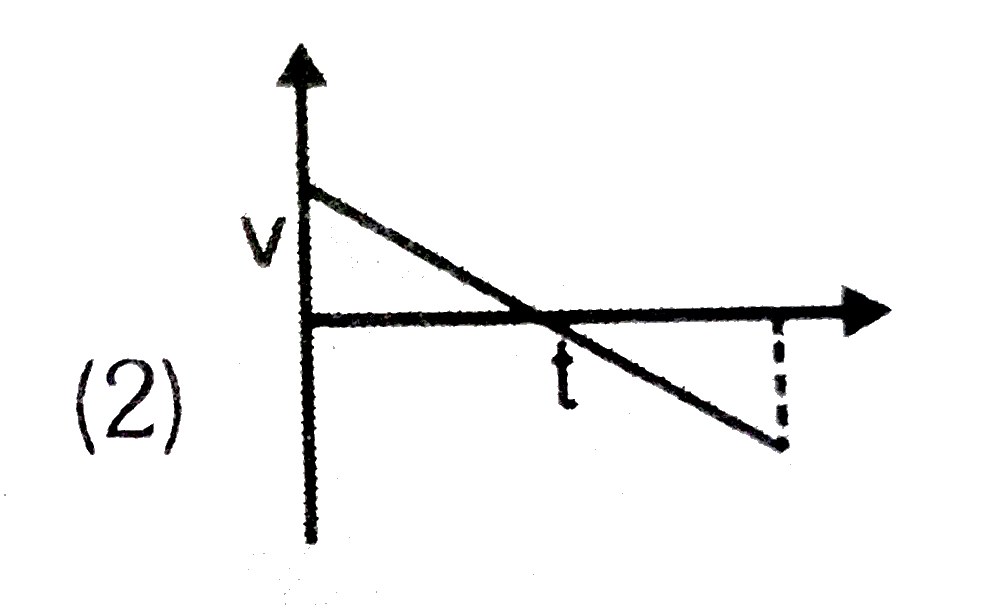 C
C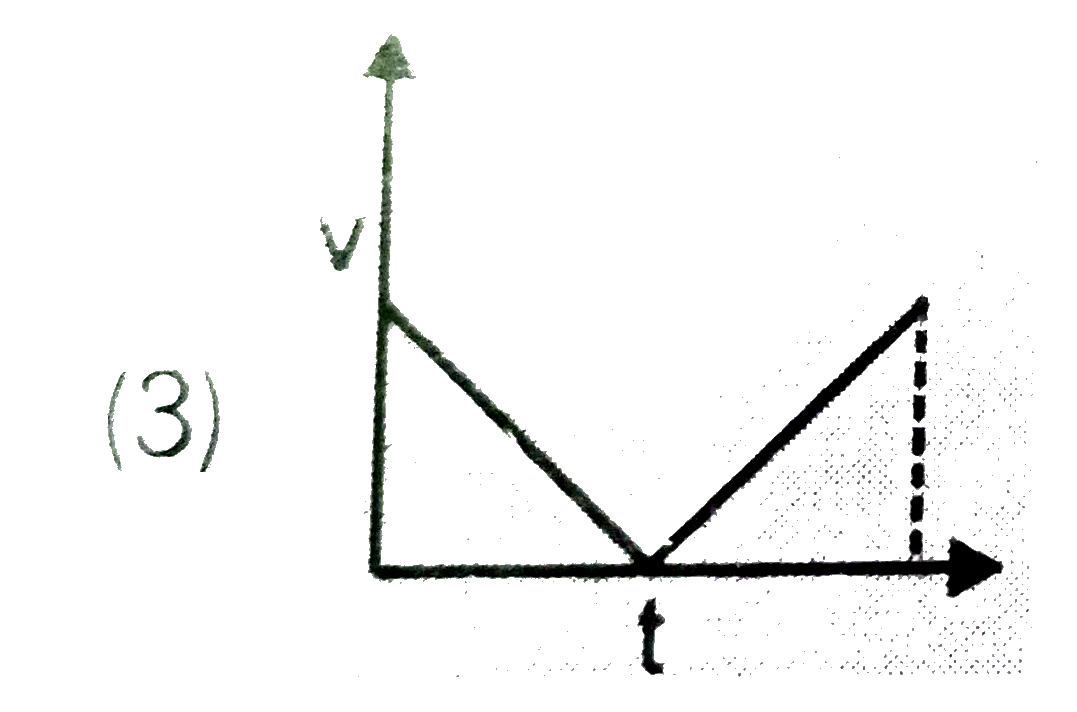 D
D
A body is thrown vertically upwards and then falls back on the ground. Its potential energy is maximum
View SolutionA body is thrown vertically upwards with a velocity u . Find the true statement from the following
View SolutionA body is thrown vertically upward with velocity u, the greatest height h to which it will rise is
View SolutionA body is thrown vertically upwards and takes 5 seconds to reach maximum height. The distance travelled by the body will be same in :-
View SolutionA ball is thrown vertically upwards from the ground. Work done by air resistance during its time of flight is
View Solution
