Five forces →F1,→F2,→F3,→F4 , and →F5 , are acting on a particle of mass 2.0kg so that is moving with 4m/s2 in east direction. If →F1 force is removed, then the acceleration becomes 7m/s2 in north, then the acceleration of the block if only →F1 is action will be:
16m/s2
√65ms2
√260ms2
√233ms2
The correct Answer is:B
→F1+→F2+→F3+→F4+→F5=2(4ˆi) .
and →F2+→F3+→F4+→F5=2(7ˆj) .
From (i) and (ii), →F1=8ˆi−14ˆj .
→a=→F1m=4ˆi−7ˆj .
implies a1=√16+49=√65m/s2 .
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Linear Momentum And Impulse
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle
19 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
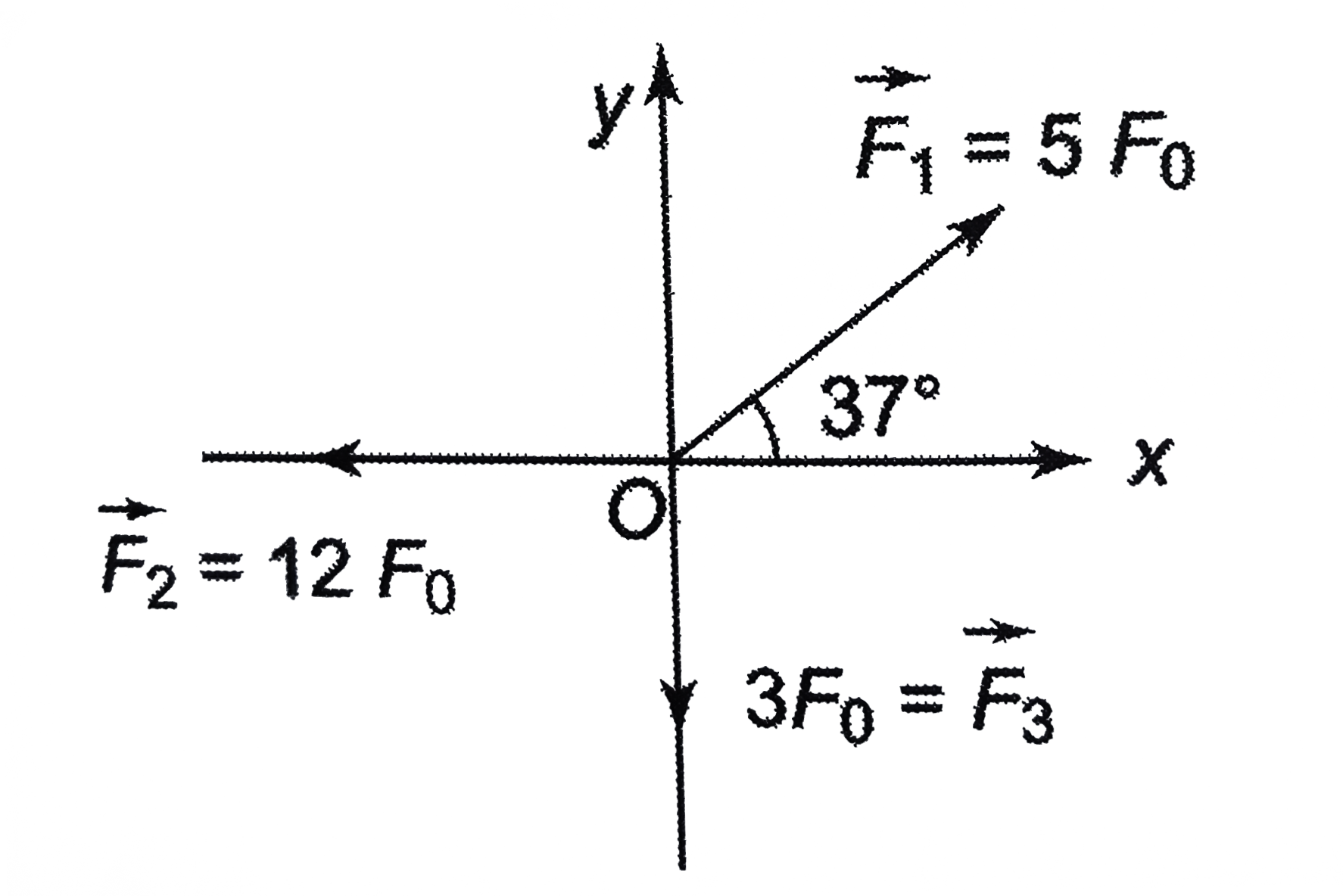
Find the resultant of −→F1+−→F2−−→F3(sin37∘=35,cos37∘=45)
View SolutionA moving particle of mass m is acted upon by five forces→F1,→F2,→–––(F)3,→F4 and →F5. Forces →F2 and →F3 are conservative and their potential energy functions are U and W respectively. Speed of the particle changes from Va to Vb when it moves from position a to b. Which of the following statement is/are true – (a) Sum of work done by →F1,→F4 and →F5=Ub−Ua+Wb−Wa
(b) Sum of work done by →F1,→F4 and →F5=Ub−Ua+Wb−Wa+12m(V2a−V2a)
(c) Sum of work done by all five forces =12m(V2b−V2a)
(d) Sum of work done by →F2 and →F3=(Ub+Wb)−(Ua+Wa)
View Solution
Knowledge Check
When force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/mWhen forces F1, F2, F3, are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed then the acceleration of the particle is
A(a) F/mB(b) F2F3/mF1C(c) (F2−F3)/mD(d) F2/mWhen force −→F1,−→F2,−→F3…...−→Fn act on a particle , the particle remains in equilibrium . If −→F1 is now removed then acceleration of the particle is
A−→F1mB−−→F1mC−−→F2+−→F3+.....−→Fn−−→F1mD−→F1m
A particle of m=5kg is momentarily at rest at x=att=. It is acted upon by two forces →F1 and →F2. Vec(F)1=70ˆj N. The direction and manitude of →F2 are unknown. The particle experiences a constant acceleration, →a,in the direction as shown in (figure) Neglect gravity.
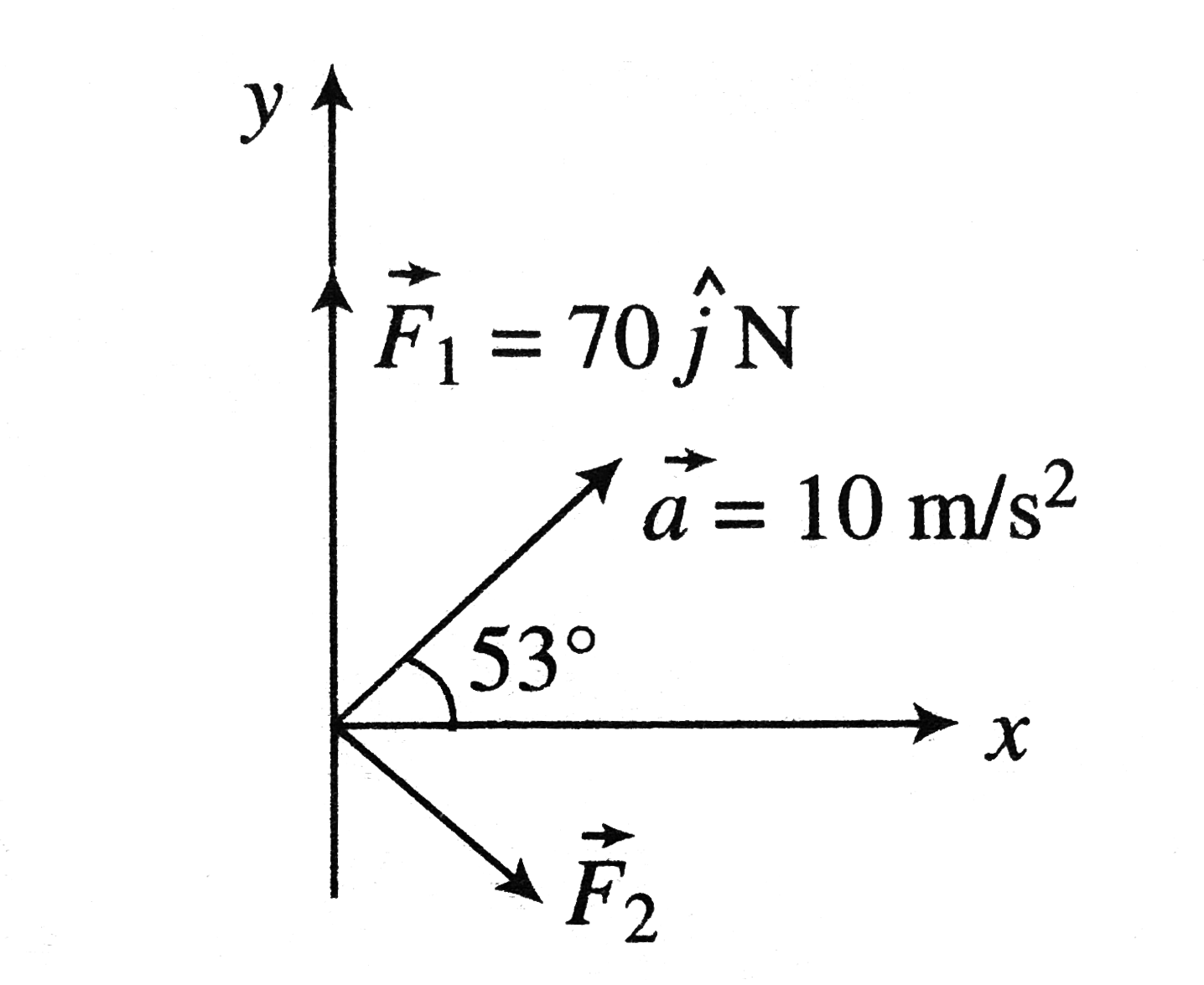
a.Find the missing force →F2.
b. What is the velocity vector of the particle at t=10s?
c. What third force, →F3 is required to make the acceleration of the particle zero? Either give magnitude and direction of →F3 or its components.
View SolutionThree forces (→F1,→F2,→F3) are acting an a particle moving vertically up with constant speed. Two force →F1=−10ˆjN, and →F1=−6ˆi=8ˆj , N are acting an particle on acting on particle respectively find →F3.
View SolutionTwo forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
View SolutionThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
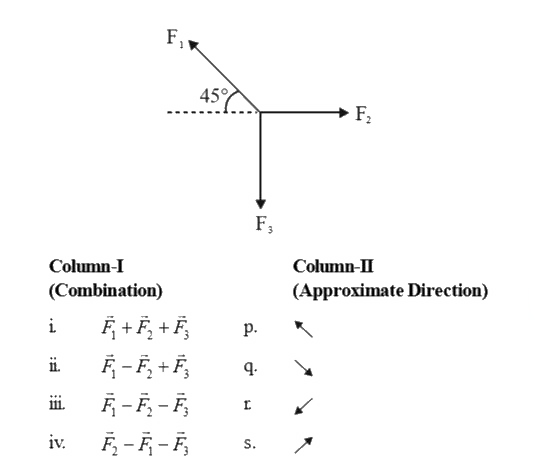
Now match the given columns and select the correct option from the codes given below.
View SolutionIf the direction of position vector →r is towards south and direciton of force vector →F is towards east, then the direction of torque vector →τ is
View Solution
