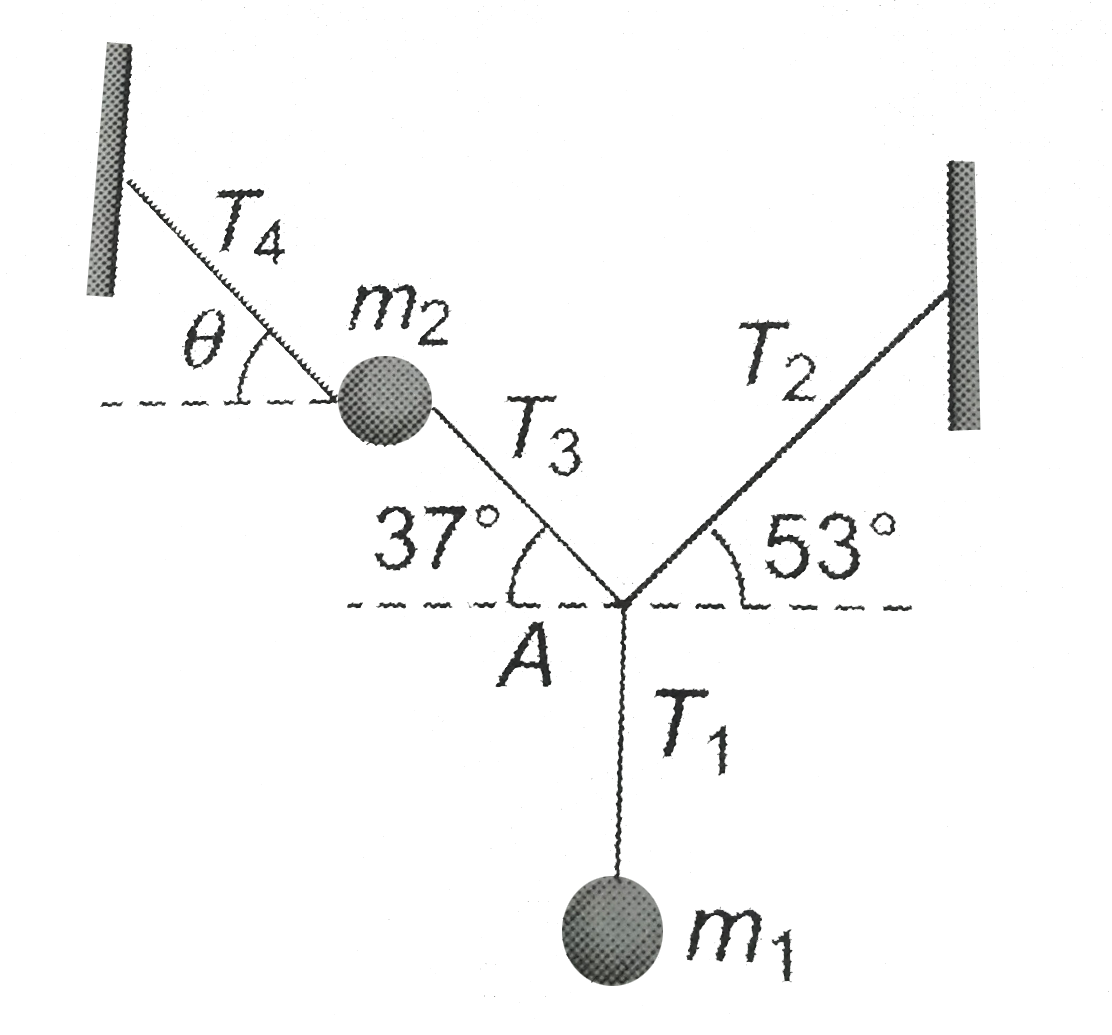
Two masses and are attached with strings as shown. For the system to be in equilibrium we have.

The correct Answer is:A
:.
Further,
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Applications Of Newton'S Laws Of Motion33videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Basic Concept Of Static And Kinetic Frictions45videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Linear Momentum And Impulse20videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test29videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
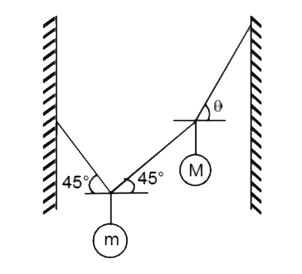
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
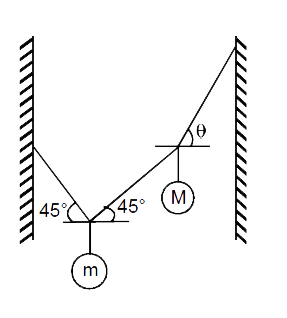 Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM - Question 2 - Select One
Two bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
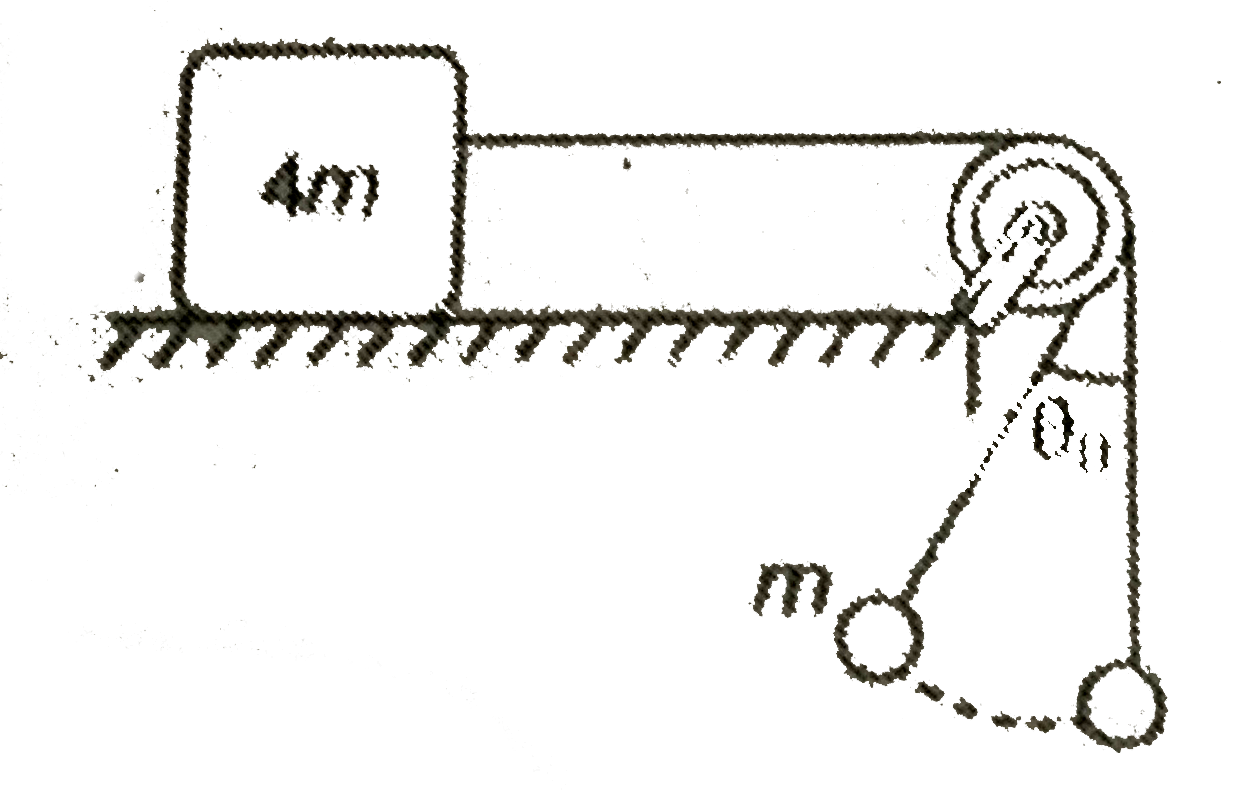 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04) - Question 3 - Select One
Two objects A and B of masses mA and mB are attached by strings as shown in fig. If they are given upward acceleration then the rato of tension T1:T2 is-
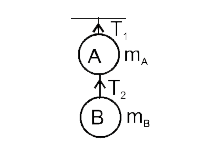 A(mA+mB)/mBB(mA+mB)/mACmA+mBmA−mBDmA−mBmA+mB
A(mA+mB)/mBB(mA+mB)/mACmA+mBmA−mBDmA−mBmA+mB
Two block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is ρ. The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator.
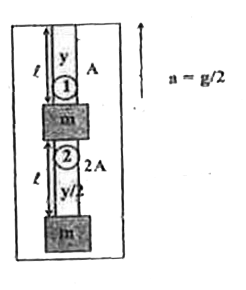
Ratio of elongation in rod 1 to that of rod 2 will beView SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is ρ. The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator.
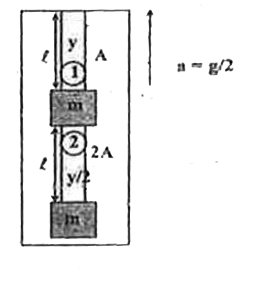
Ratio of PE stored in string-1 to string-2 in equilibrium isView SolutionA long rod ABC of mass "m" and length "L" has two particles of masses "m" and "2m" attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with A hinged at the bottom is
 .View Solution
.View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in figure. m1>m2 then the reading of spring balance will be .
 .View Solution
.View SolutionTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
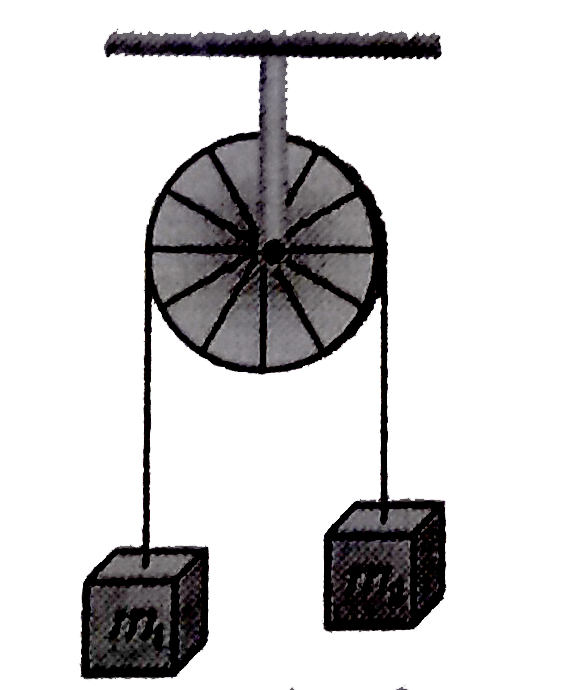 View Solution
View Solution