A force →F=(3xN)ˆi+(4N)ˆj, with x in meter, acts on a particle, changing only the kinetic energy of the particle. How mcuh work is done on the particle as it moves from coordinates (2m,3m,5m) to (3m,0m,6m)? Does the speed of the particle increase, decrease, or remain the same?
−7J
zero
+7J
+19J
The correct Answer is:C
→F=3x2ˆi+4ˆj
→r=xˆi+yˆi∵→dr=dxˆi+dyˆj
Work done,
W=∫→F.d→r
=(30)∫(23)(3x3ˆi=4ˆj).(dxˆi+dyˆj)
=(30)∫(23)3x2dx+4dy=(30)∫(20)d(x3+4y)
=[x3+4y](30)(23)=32+4×0−(23+4×3)
=27+0−(8=12)=27−20=+7j
According to work -energy theorem,
Change in the kinetic energy=Work done, W=+7J.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Potential Energy, Conservative And Non-Conservative Forces
28 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Conservation Of Mechanical Energy And Linear Momentum
24 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
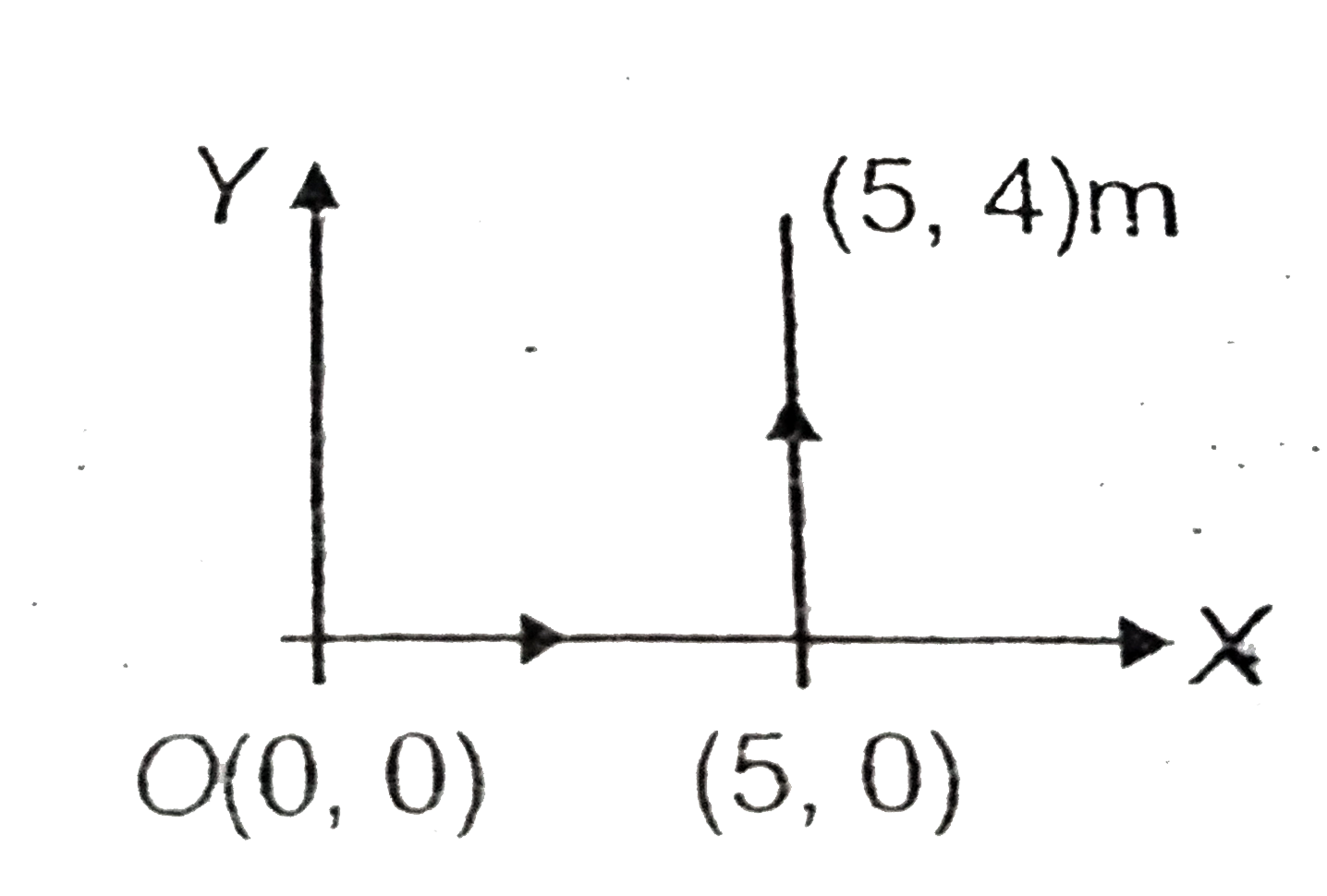
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionForce acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View Solution
Knowledge Check
Force F=[3x2ˆi+4ˆj] N where , x in metres, acts on a particle. How much work is done on the particle as it moves from coordinates (2m,3m) to (3m, 0m)?
A7JB5JC14 JD8 JA force F=(3xˆi+4ˆj) Newton (where x is in metres) acts on a particle which moves from a position (2m, 3m) to (3m, 0m). Then the work done is
A7.5 JB−12JC−4.5JD+4.5JA force →F=(5ˆi+3ˆj+2ˆk)N is applied over a particle which displaces it from its origin to the point →r=(2ˆi−ˆj)m. The work done on the particle in joules is-
A−7B+7C+10D+13
A force →F=xˆi+y2ˆjN acts on a particle and the particle moves from (1,2)m to (–3,4)m. Find work done by the force →F.
View SolutionA force →F=(5ˆi+3ˆj)N is applied over a particle which displaces it from its original position to the point →s=S(2ˆi−1ˆj)m. The work done on the particle is
View SolutionA force →F=(6ˆi−8ˆj)N, acts on a particle and displaces it over 4m along the X-axis and 6m along the Y-axis. The work done during the total displacement is
View SolutionA variable force, given by the 2-dimensional vector F=(3x2ˆi+4ˆj), acts on a particle. The force is in newton and x is in metre. What is the change in the kinetic energy of the particle as it moves from the point with coordinates (2, 3) to (3, 0)? (The coordinates are in metres)
View SolutionA force acting on particle is given by →F=(3x2ˆi+4yˆj)N. The change in kinetic energy of particle as it moves from (0,2m) to (1m,3m) is
View Solution
