A force acting on particle is given by →F=(3x2ˆi+4yˆj)N. The change in kinetic energy of particle as it moves from (0,2m) to (1m,3m) is
6J
10J
11J
13J
The correct Answer is:C
To solve the problem of finding the change in kinetic energy of a particle moving under the influence of a variable force, we can follow these steps:
1. Identify the Force and Displacement:
The force acting on the particle is given by:
→F=(3x2^i+4y^j)N
The particle moves from the point (0,2m) to (1m,3m).
2. Work-Energy Theorem:
According to the work-energy theorem, the work done by the force on the particle is equal to the change in kinetic energy:
W=ΔKE
3. Expression for Work Done:
The work done by a force during a displacement can be expressed as:
W=∫→F⋅d→r
where d→r is the differential displacement vector.
4. Parameterize the Path:
The displacement d→r can be expressed in terms of dx and dy:
d→r=dx^i+dy^j
5. Dot Product of Force and Displacement:
Now, we can calculate the dot product:
→F⋅d→r=(3x2^i+4y^j)⋅(dx^i+dy^j)=3x2dx+4ydy
6. Set Up the Integral:
The work done can now be calculated by integrating from the initial to the final position:
W=∫(1,3)(0,2)(3x2dx+4ydy)
We will do this in two parts: one for x from 0 to 1 and the other for y from 2 to 3.
7. Calculate the Work Done:
We can split the integral:
W=∫103x2dx+∫324ydy
- First Integral:
∫103x2dx=3(x33)10=3(133−0)=1
- Second Integral:
∫324ydy=4(y22)32=4(322−222)=4(92−42)=4(52)=10
8. Total Work Done:
Now, add the results of the two integrals:
W=1+10=11J
9. Change in Kinetic Energy:
From the work-energy theorem:
ΔKE=W=11J
Final Answer:
The change in kinetic energy of the particle as it moves from (0,2m) to (1m,3m) is:
ΔKE=11J
The force acting on the particle is given by:
→F=(3x2^i+4y^j)N
The particle moves from the point (0,2m) to (1m,3m).
According to the work-energy theorem, the work done by the force on the particle is equal to the change in kinetic energy:
W=ΔKE
The work done by a force during a displacement can be expressed as:
W=∫→F⋅d→r
where d→r is the differential displacement vector.
The displacement d→r can be expressed in terms of dx and dy:
d→r=dx^i+dy^j
Now, we can calculate the dot product:
→F⋅d→r=(3x2^i+4y^j)⋅(dx^i+dy^j)=3x2dx+4ydy
The work done can now be calculated by integrating from the initial to the final position:
W=∫(1,3)(0,2)(3x2dx+4ydy)
We will do this in two parts: one for x from 0 to 1 and the other for y from 2 to 3.
We can split the integral:
W=∫103x2dx+∫324ydy
∫103x2dx=3(x33)10=3(133−0)=1
∫324ydy=4(y22)32=4(322−222)=4(92−42)=4(52)=10
Now, add the results of the two integrals:
W=1+10=11J
From the work-energy theorem:
ΔKE=W=11J
The change in kinetic energy of the particle as it moves from (0,2m) to (1m,3m) is:
ΔKE=11J
Topper's Solved these Questions
Similar Questions
A single conservative force acting on a particle varies as →F=(−Ax+Bx2)ˆiN, where A and B are constants and x is in meters. (a) Calculate the potential energy function U(x) associated with this force, taking U=0 at x=0. (b) Find the change in potential energy and the change in kinetic energy of the system as the particles moves from x=2.00m to x=3.00m.
View SolutionA particle is acted upon by a force →F=yˆi+xˆj newton. When the particle is moved from (1 m, 1 m) to (9m, 3 m) via straight path, work done by →F is y. What is the value of xy?
View Solution
Knowledge Check
A variable force, given by the 2-dimensional vector F=(3x2ˆi+4ˆj), acts on a particle. The force is in newton and x is in metre. What is the change in the kinetic energy of the particle as it moves from the point with coordinates (2, 3) to (3, 0)? (The coordinates are in metres)
A−7JBZeroC+7JD+19JA varable force, given by the 2- dimensional vector¯¯¯F=(3×2ˆi+4ˆj), acts on a particle. The force is in newton and x is in metre. What is the change in the kinetic energy of the particle as it moves from the point with coordinates (2,3) to (3,0) (The coornates are in metres)
A−7JBzeroC+7JD+19JThe graph given below shows how the force on a mass depends on the position of the mass. What is the change in the kinetic energy of the mass as it moves from x=0.0m to x=3.0m ?
 A0.0JB20JC50JD60J
A0.0JB20JC50JD60J
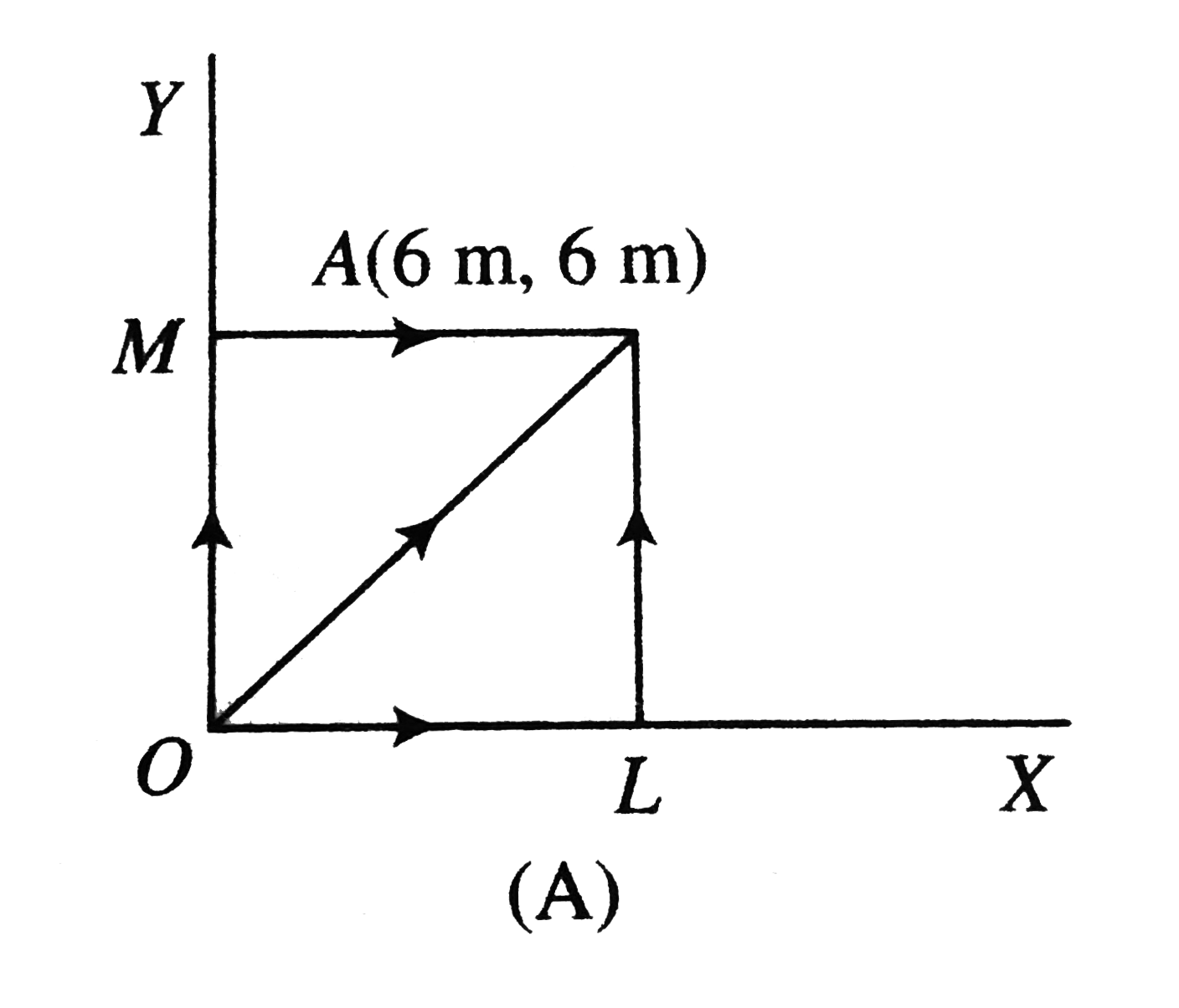
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.
If the potential energy at O is 16J, the potential energy at A will be
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.

Speed of the particle at A will be nearly
View SolutionPassage I) In simple harmonic motion force acting on a particle is given as F=−4x, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is −16ms2. Mass of the particle is 0.5 kg.
At x=+1m, potential energy and kinetic energy of the particle are
View SolutionA force F=(3xˆi+4ˆj) Newton (where x is in metres) acts on a particle which moves from a position (2m, 3m) to (3m, 0m). Then the work done is
View SolutionA particle is acted upon by only a conservative force F=(7ˆi−6ˆj) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
View Solution
