A block of mass m is pulled slowly by a minimum constant force (F) on a horizontal surface thorugh a distance x. The coefficient of kinetic friciton is μ. Find the work done by the force (F).

μmgx1+μ2
μmgx1−μ2
μmgx√1+μ2
None of these
The correct Answer is:A
The work done by the force F is
W=Fmin×cosθ ...(i)
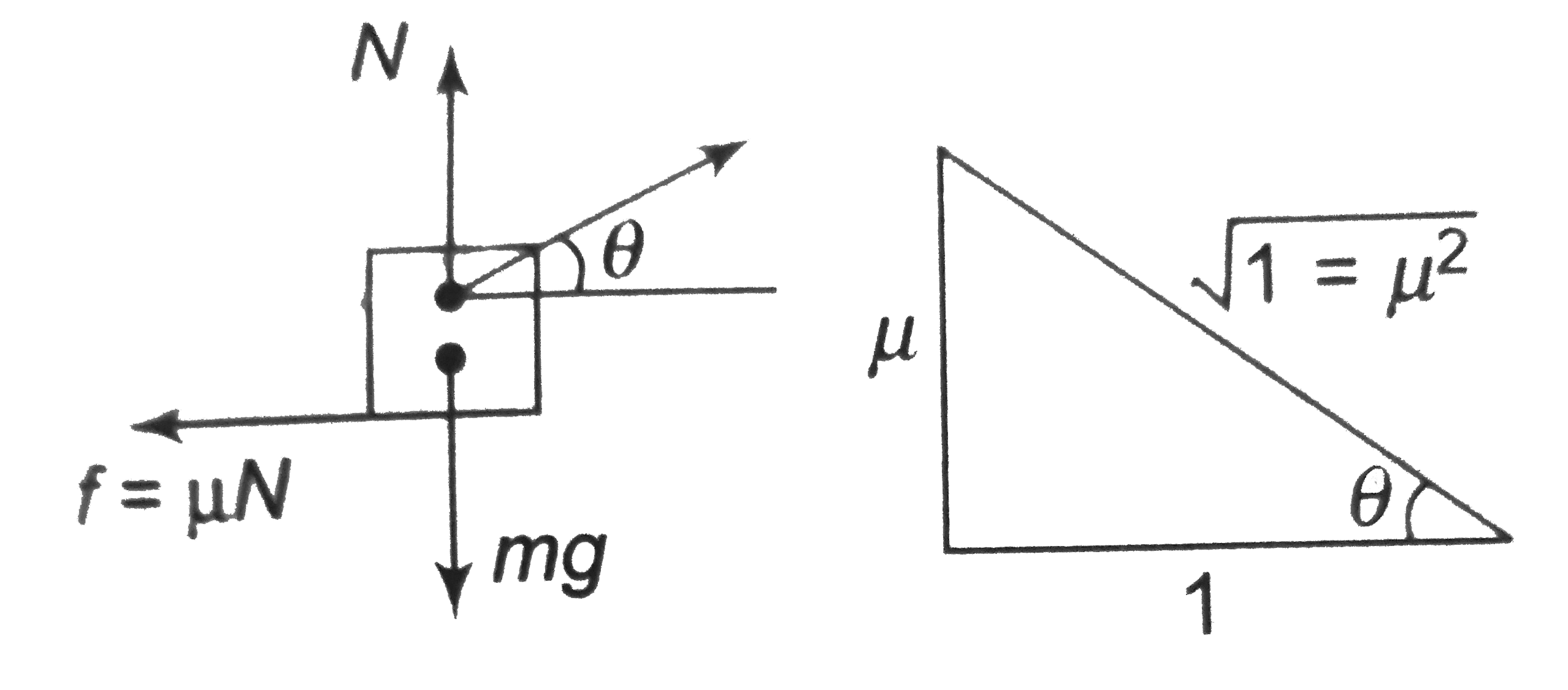
cosθ=1√1+e2sinθ=μ√1+e2
F is minimum when tanθ=μ (ii)
Fmin=mgsinθ (iii)
Using equation (i) and (iii).
W=(mgsinθ)×cosθ
=mg=μ√1+μ2×1√1+μ2=μmgx(1+μ2).
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Assertion Reasoning
Explore 17 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:NEET Questions
Explore 49 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Collision
Explore 31 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
View Solution
Knowledge Check
A block of mass m is pulled slowly by a minimum constant force on a rough (μ) horizontal surface through a distance x. Find work done by force F.
Amgx√1+μ2Bμmgx1+μ1Cμ2mgx√1+μ2Dmgx(1+μ2)A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
AThe maximum velocity of the block during the motion is PμmgBThe maximum velocity of the block during the motion is P2μmgCThe block's speed is never decreasing and finally becomes constantDThe speed of the block first increases to a maximum value and then decreasesA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNone
A block of mass m is kept over another block of mass 2m and the system rests on a smooth horizontal surface. The coefficient of friction between the block is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement the of the system when a force mg is applied to the lower block
View SolutionA crate of mass m is pulled with a force F along a fixed right angles horizontal trough as in figure. The coefficient of kinetic friction between the crate and the trough is μ. Find the value of force F required to pull it along the trough with constant velocity.

View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m is kept on a rough horizontal surface. It is moved through a distance (s) by applyig a force F in the horizontal direction. What is the work done by the normal reaction?
View Solution