At t=0, the positions and velocities of two particles are as shown in the figure. They are kept on a smooth surface and being mutually attracted by gravitational force. Find the position of centre of mass at t=2s.
 .
.
A
X = 5 m
B
X = 7 m
C
X = 3 m
D
X = 2 m
Video Solution
Text Solution
The correct Answer is:B
(b) As no external force are acting on the system. The velocity of centre of mass will be constant.
vcm=1×5−1×31+1=1m/s
Displacement of centre of mass Δxcm=1×2=2m
Hence position of centre of mass Δxcm=5+2=7m.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia39videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Rotational Kinematics19videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2s is :
 A0.2kgms−1B0.02kgms−1C0.1kgms−1D0.4kgms−1
A0.2kgms−1B0.02kgms−1C0.1kgms−1D0.4kgms−1 - Question 2 - Select One
The figure shows the positions and velocity of two particle. If the paritcle move under the mutual attraction of each other, then the position of centre of mass at t=1s is :-
 Ax=5mBx=6mCx=3mDx=2m
Ax=5mBx=6mCx=3mDx=2m
Find the position of centre of mass of the section shown in figure
 View Solution
View SolutionFind out the position of centre of mass of the figure shown below.
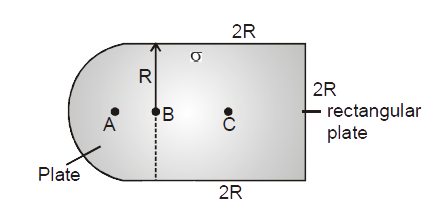
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
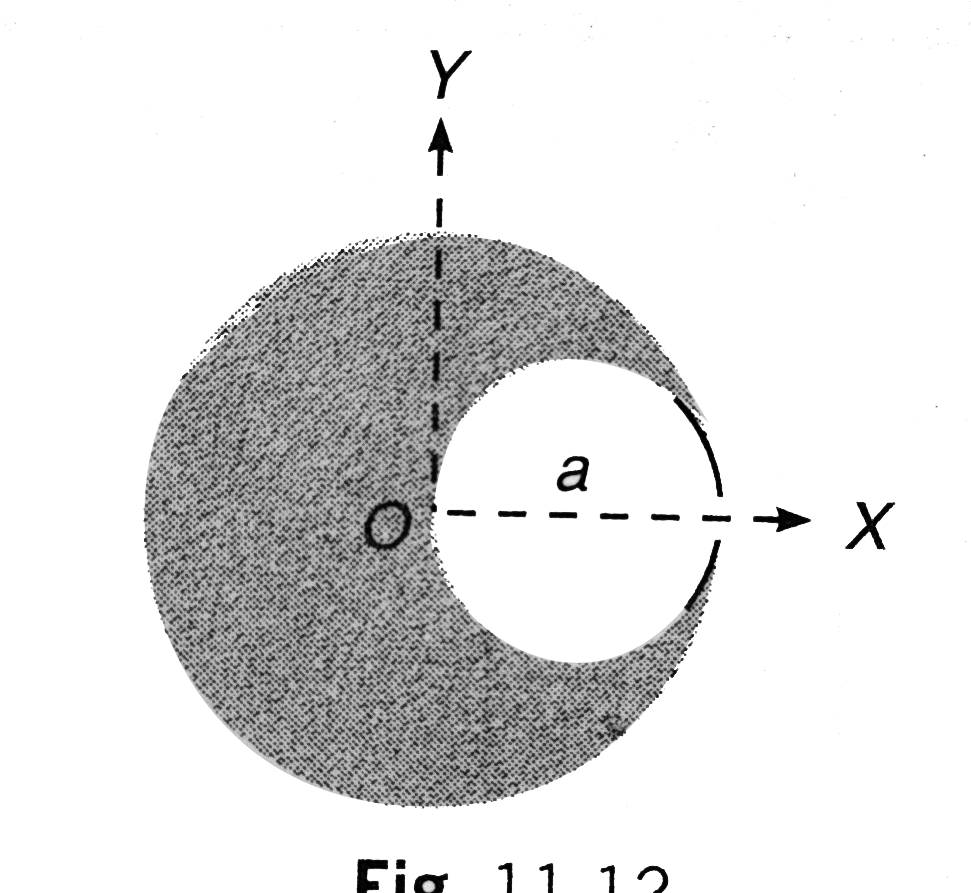 View Solution
View SolutionFind out the position of centre of mass of the uniform lamina as shown in figure.
 View Solution
View SolutionFind the position of centre of mass of the T-shaped plate from O, in Fig.
 View Solution
View SolutionFigure shows position and velocities of two particles moving under mutual gravitational attraction in space at time t=0. The position of centre of mass after one second is (in meters)
.
 View Solution
View Solution

