If a graph is plotted between T2 and r3 for a planet, then its slope will be be (where MS is the mass of the sun)
4πGMS
GMS4π
4πGMS
GMS
The correct Answer is:A
Time period of a revolution of a planet,
T=2πrr=2πr√GMSr=2πr3/2√GMS
Where MS is the mass of the sun. Squaring both sides, we get
T2=4π2r3GMS
The graphs between T2andr3 is a straight line whose slope is 4π2GMS
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Gravitational Field And Acceleration Due To Gravity34videos
GRAVITATION
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Gravitational Potential, Energyand Escape Velocity32videos
GRAVITATION
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test30videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test29videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If a graph is plotted for the square of period (T2) and mass attached to a spring, its shape will be
A B
B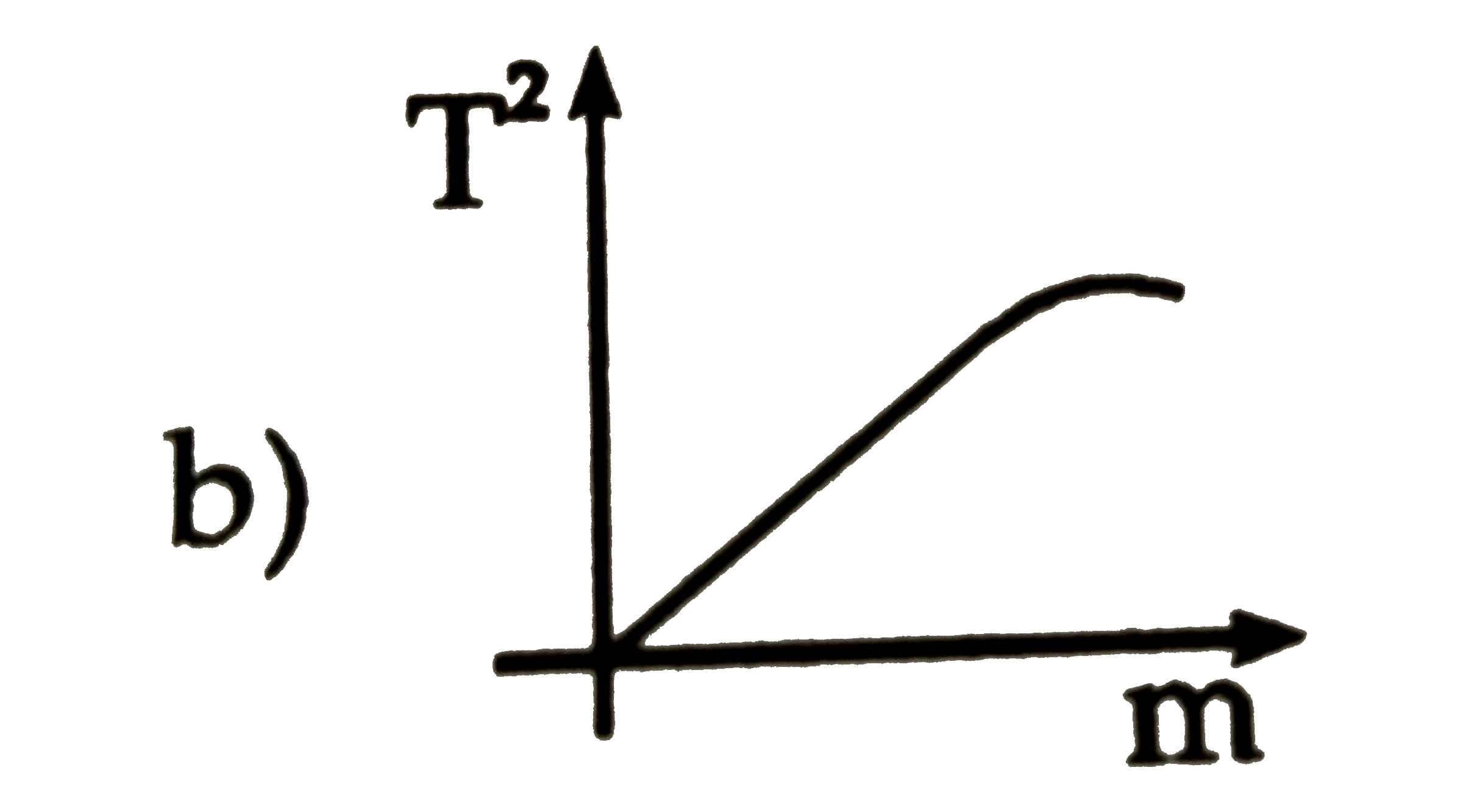 C
C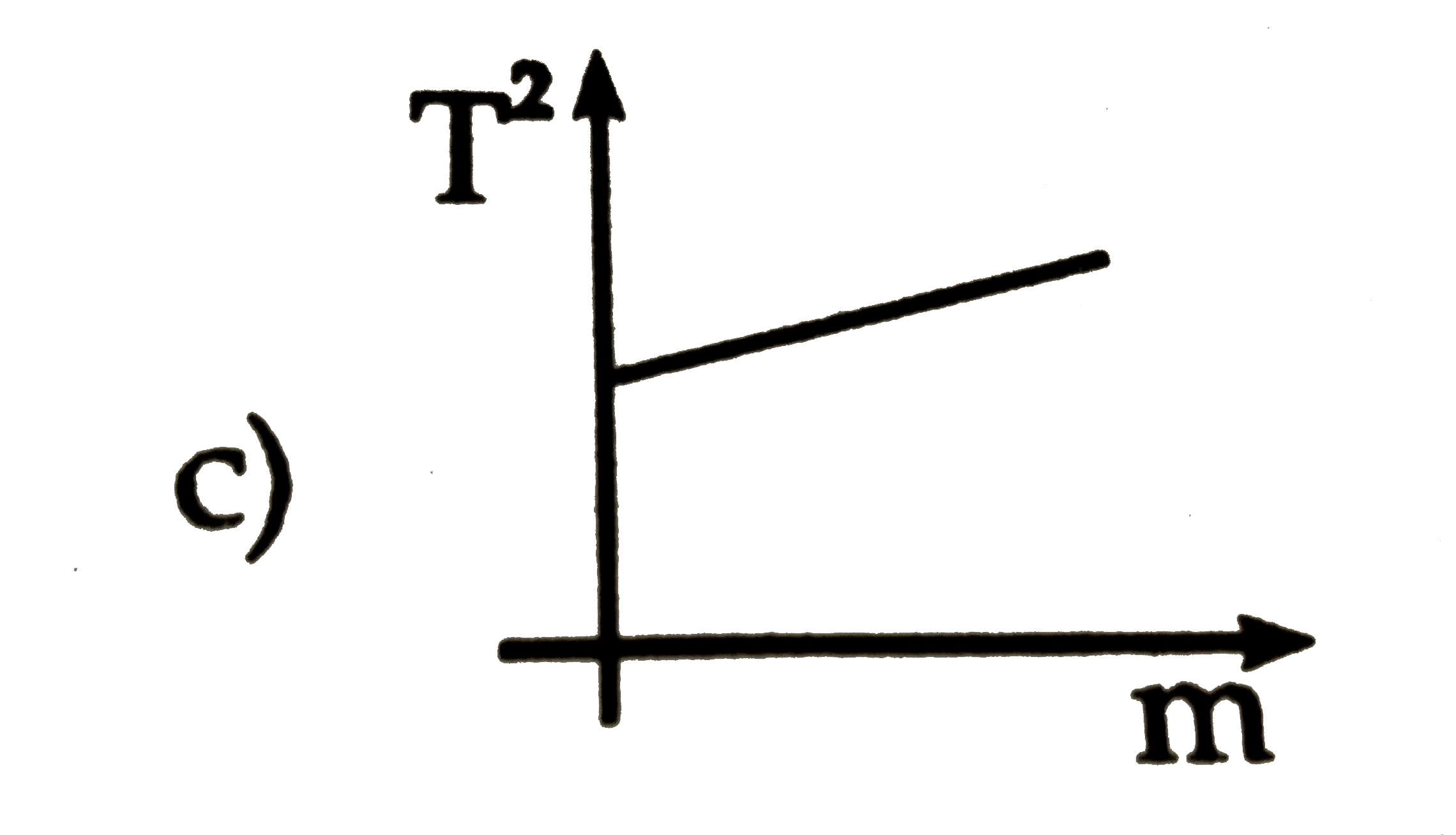 D
D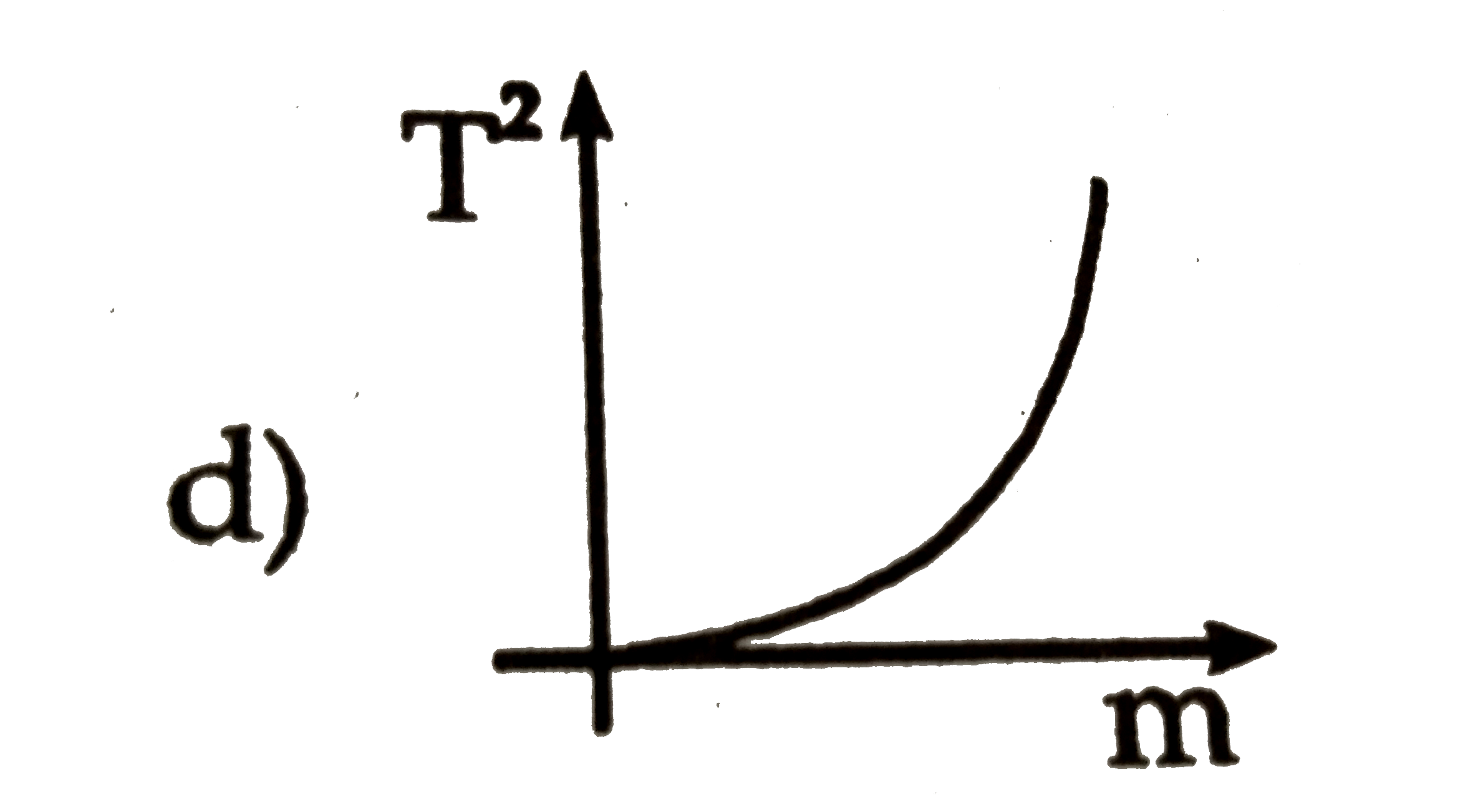
- Question 2 - Select One
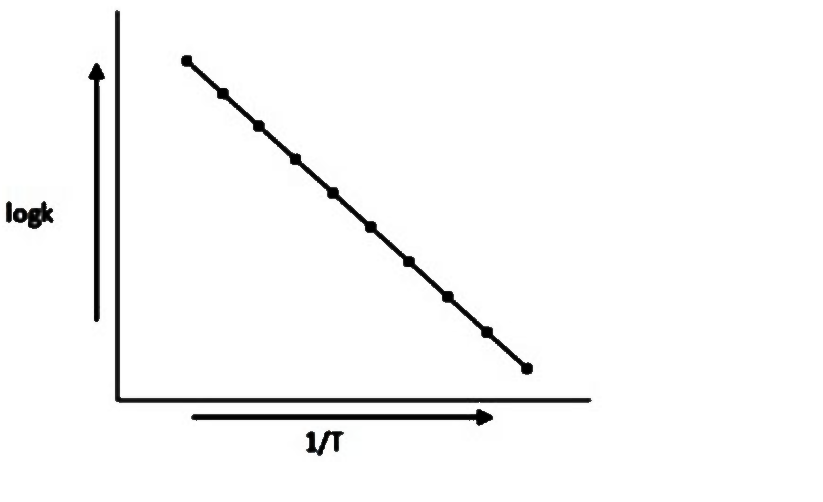
If a graph is plotted between ln k and 1/T for the first order reaction, the slope of the straight line so obtained is given by
A−EaRB−Ea2.303RC−2.303EaRD−Ea2.303 - Question 3 - Select One
In Arrehenius equation if a graph is plotted between logK and 1/T, the slope of the curve will be:
A−EaRB−Ea2.303RCEaRDEa2.303R
If we plot a graph between log K and 1T by Arrhenius equation , the slope is
View SolutionFor a first order reaction, when a graph is plotted between log10([A])0([A])t on y-axis and time (t) on x-axis , slope of the graph of the graph is equal to __________.
View SolutionA graph is plotted between p (atm) vs t∘C for 10 mol of an ideal gas as follows:
Then slope of curve and volume of container (L) respectively, are:
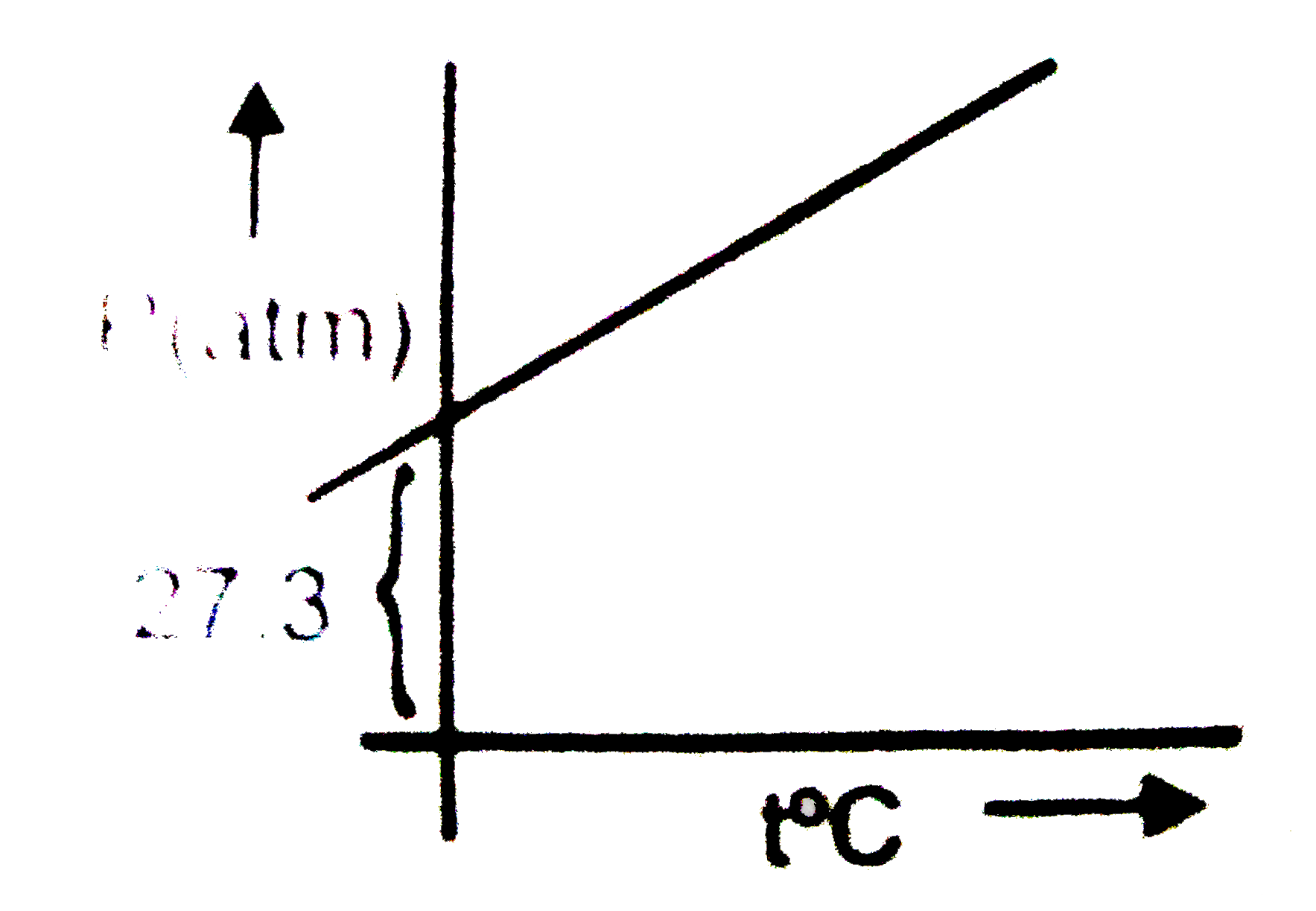 View Solution
View SolutionFor a planet, the graph of T2 against r3 is plotted. The slope of the graph is
View SolutionKepler's third law states that the square of period of revolution (T) of a planet around the sun, is proportional to third power of average distance, r between the sun and the planet i.e.
T2=Kr3
Here, K is constant.
If masses of the sun and the planet are M and m respectively, then as per Newton's law of gravitation, force of attraction between them is F=GMmr2 where G is gravitational constant.The relation between G and K is described asView Solution