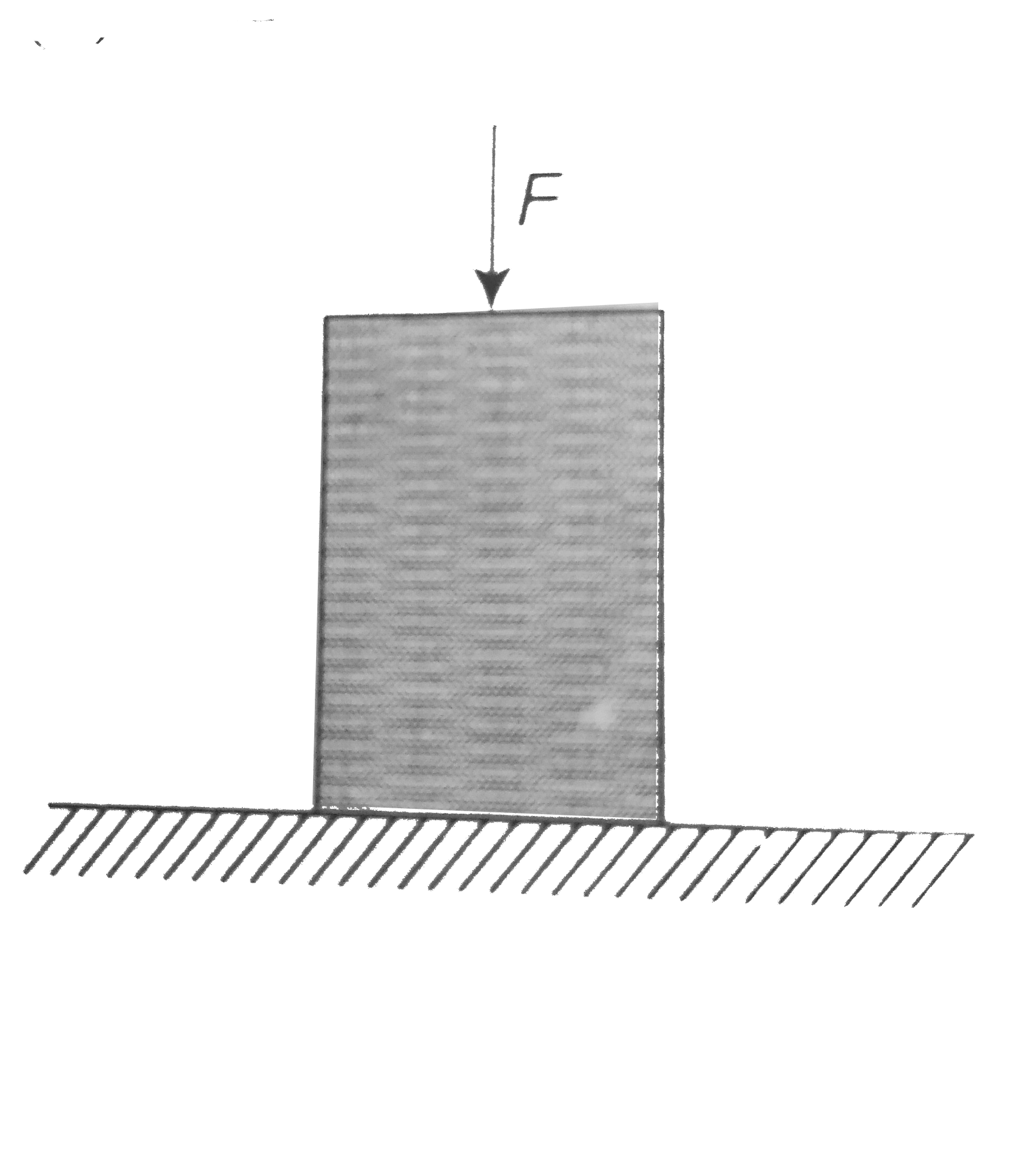
A metal cylinder of length L is subjected to a uniform compressive to a uniform compressive force F as shown in the figure. The material of the cylinder has Young's modulus Y and poisson's ratio σ The change in volume of the cylinder is
σFLY
(1−σ)FLY
(1+2σ)FLY
(1−2σ)FLY
The correct Answer is:D
Volume of the cylinder,
V=πr2L
Volumetric strain =△VV=△(πr2L)πr2L
=△VV=πr2△L+2πrL△rπr2L
=△LL+2△rr
Poisson's ratio, σ=(△rr)(△LL)
or △rr=−σ△LL
On substituting this value of △rr in Eq. (i) we get
△VV=△LL(1−2σ) .(ii)
Young's modulus, Y=(Fπr2)(△LL)
Or △LL=Fπr2Y
On subsitituting this value of △LL in Eq. (ii) we get
△VV=Fπr2Y(1−2σ)
△Vπr2L=Fπr2Y(1−2σ)
triag≤V=FLY(1−2σ)
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Assertion Reasoning
20 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - NEET Questions
17 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Viscosity
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
A cylinder of radius r and length l is placed in an uniform electric field parallel to the axis of the cylinder. The total flux for the surface of the cylinder is given by-
View SolutionA solid copper cylinder of length l=65cm is placed on a horizontal surface and subjected to a vertical compressive force F=1000N directed downward and distributed uniformly over the end face. What will be the resulting change of the volume of the cylinder in cubic millimeters?
View Solution
Knowledge Check
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
A2πR2EBπR2/EC(πR2−πR)EDzeroA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
A2πR2EBπR2/EC(πR2/πR)/EDZeroA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
AZeroB2πR2EC2πRLED(2πR2+2πRL)E
A very long, solid insulating cylinder with radius R has a cylindrical hole with radius a bored along its entire length. The axis of the hole is at a distance b from the axis of the cylinder, where a<b<R (as shown in figure). The solid material of the cylinder has a uniform volume charge density ρ. Find the magnitude and direction of the electric field inside the hole, and show that this is uniform over the entire hole.
 .
.
View SolutionA square sheet of edge length L and uniform mass per unit area (σ) is used to form a hollow cylinder.The moment of inertia of this cylinder about the central axis is
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
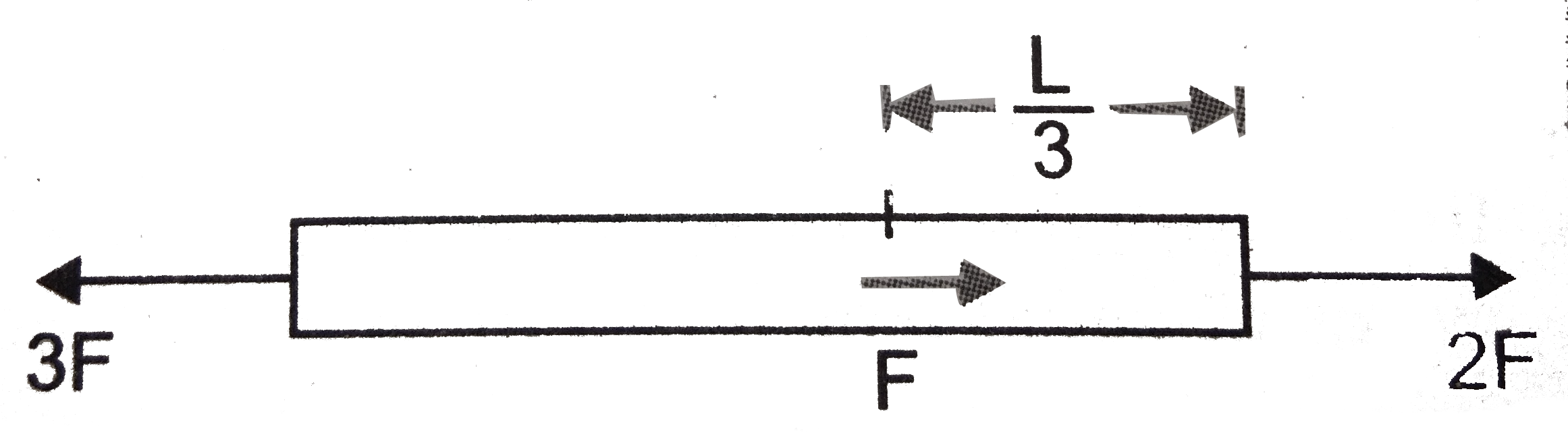
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
View SolutionA cylinder of length l and radius r is heated to temperature T. A longitudeinal compressive force F is applied on cylinder to keep its length same. Find coefficient of volume expansion.
View Solution
