A metal wire of length L1 and area of cross section A is ttached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
[(Y1Y2)A][2(Y1L2+Y2L1)]
([Y1Y2)A)](L1L2)12
[(Y1Y2)A](Y1L2+Y2L1)
[(Y1Y2)12A](L1L2)12
The correct Answer is:C
Using the usual expression for the Young's modulus the force constant for the wire can be written as
k=F△L=YAL
Where the symbols have their usul meanings, When the two are connected together in series, the effective force constant is given by
keq=k1k2k1+k2
Substituting the corresponding lengths, area of cross section and the Young's moduli, we get
keq=(Y1AL1)(Y2AL2)Y1AL1+Y2L2=(Y1Y2)AY1L2+Y2L1
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Assertion Reasoning
20 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - NEET Questions
17 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Viscosity
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
A metal wire of length jl and area of cross - section A is fixed between rigid supports negligible tension . If this is cooled. The tension in the wire will be
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View Solution
Knowledge Check
A metal wire of length L1 and area of cross-section A is attached to a rigid support. Another metal wire of length L2 and of the same cross-sectional area is attached to free end of the first wire. A body of mass M is then suspended from the free end of the second wire. If Y1andY2 are the Young's moduli of the wires respectively, the effective force constant of the system of two wire is
A[(Y1Y2)A]/[2(Y1L2+Y2L1)]B[(Y1Y2)A]/[(L1L2)]1/2C[(Y1Y2)A]/[(Y1L2+Y2L1)]D(Y1Y2)1/2A/(L1L2)1/2An electric wire of length ‘ I ’ and area of cross-section a has a resistance R ohm s. Another wire of the same material having same length and area of cross-section 4a has a resistance of
A4RBR/4CR/16D16RA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
AMg(L1−L)ALBMgLAL1CMgLA(L1−L)DMgL1AL
A metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the torce corstant of the wire is
View SolutionOne end of a Nichrome wire of length 2L and cross-sectional area A is attatched to an end of another Nichrome wire of length L and cross-sectional area 2A. If the free end of the longer wire is at an electric potential of 8.0 volts, and the free end of the shorter wire is at an electric potential 1.0 volts, the potential at the junction of the two wires is equal to
View SolutionA mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
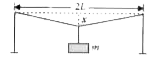
A mass m is suspended from the midpoint of the wire. Strain in the wire is
View SolutionA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
View Solution
