A uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
mω2L2AY
mω2L22AY
mω2L23AY
2mω2L22AY
The correct Answer is:C
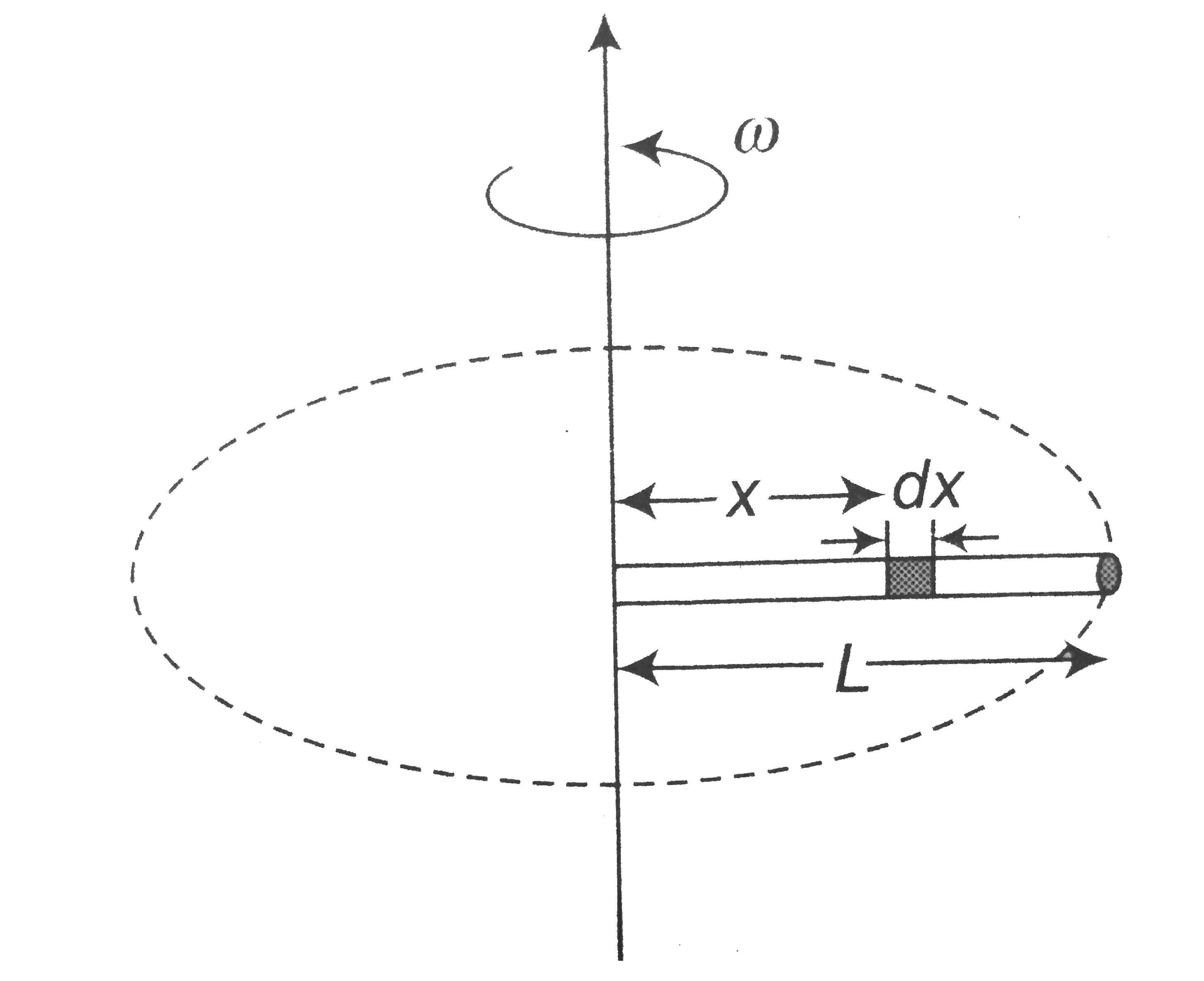
Consider a small element of length dx at a distance x from the axis of ratation.
Mass of element, dm=mLdx=μdx
Where μ=mL
The centripetal force acting on the element is
dT=dmω2x=μω2xdx
As this force is provided by tension in the rod (due to elasticity), so the tension in the rod at a distance x from the axis of rotation will be due to the cetripetal force due to all elements between x=x to x=L
T=∫Lxμω2xdx=μω22[L2−x2] .(i)
Let dl be increase in length of the element, then
Y=TAdldx
dl=TdxYA=μω22YA[L2−x2]dx .[using (i)]
So the total elongation of the whole rod is
l=∫L0μω22YA[L2−x2]dx
=μω22YA[L2x−x33]L0
=13μω2L3YA=13mω2L2YA
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Assertion Reasoning20videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - NEET Questions17videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Viscosity29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
A steel rod of length 2l cross-sectional area A and mass M is set rotating in a horizontal plane about an axis passing through its centre and perpendicular to its length with constant angular velocity ω. If Y is the Young's modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotation - Question 2 - Select One
A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AY - Question 3 - Select One
A uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity o in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
Amω2L2AYBmω2L22AYCmω2L23AYD2mω2L2AY
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA thin uniform metallic rod of length 0.5 m and radius 0.1 m rotates with an angular velocity 400rad/s is a horizontal plane about a vertical axis passing through one of its ends. Calculate (a) tenstion in the rod and (b) the elogation of te rod. The density of material of the rod is 104kg/m3 and the young's modulus is 2×1011N/m2
View SolutionA uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
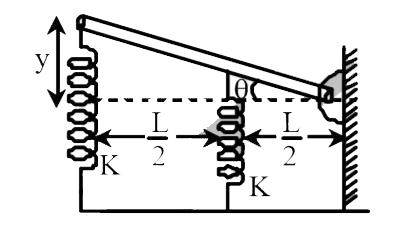
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
 View Solution
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution

