Figure shows a system consisting of a massless pulley, a spring of force constant and a block of mass . If the block is slightly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

The correct Answer is:D
Let us assume thet in equilibrium condition spring is elongate from its natural length.
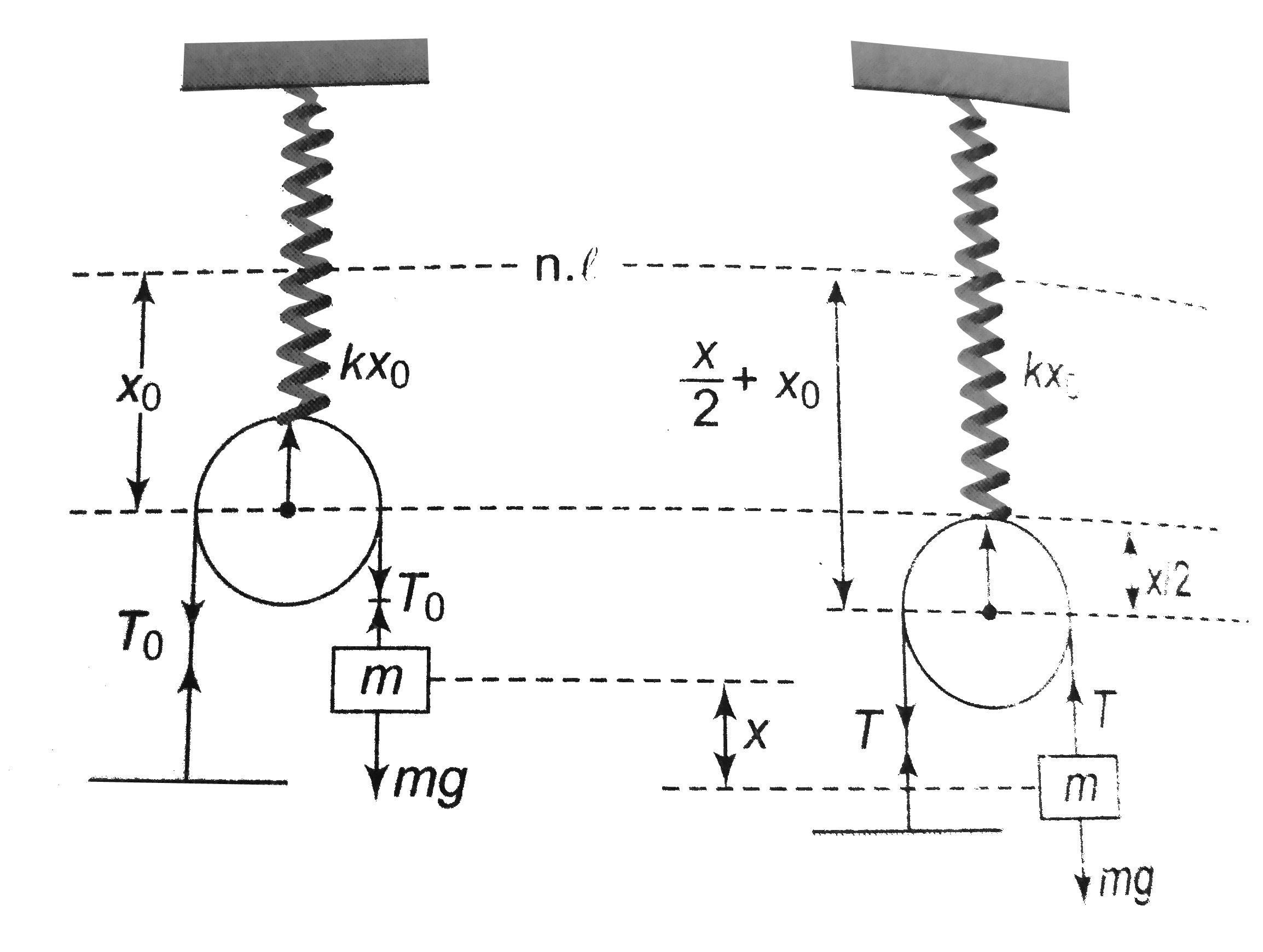
In equilibrium
and
(1)
If the mass distance from its equilibrium position then pulley will move down by so the extra force then spring will be . From figure
From eq. (1) we get
...(2)
Now compare eq. (2) with
then
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm25videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum19videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Velocity , Acceleration And Energy Of Simple Harmonic Motion40videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
Figure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
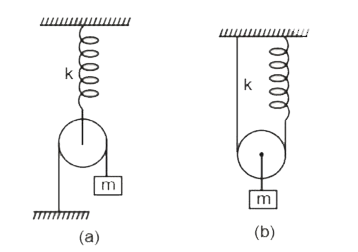 View Solution
View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
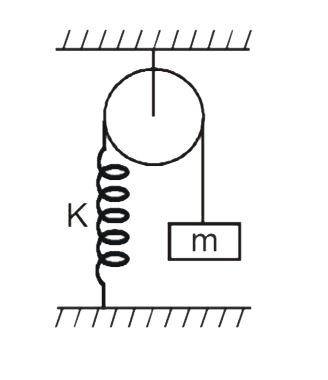 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK - Question 2 - Select One
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
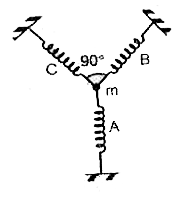 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1) - Question 3 - Select One
An elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is
 A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.
 View Solution
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is
 View Solution
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
 View Solution
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
 View Solution
View Solution
