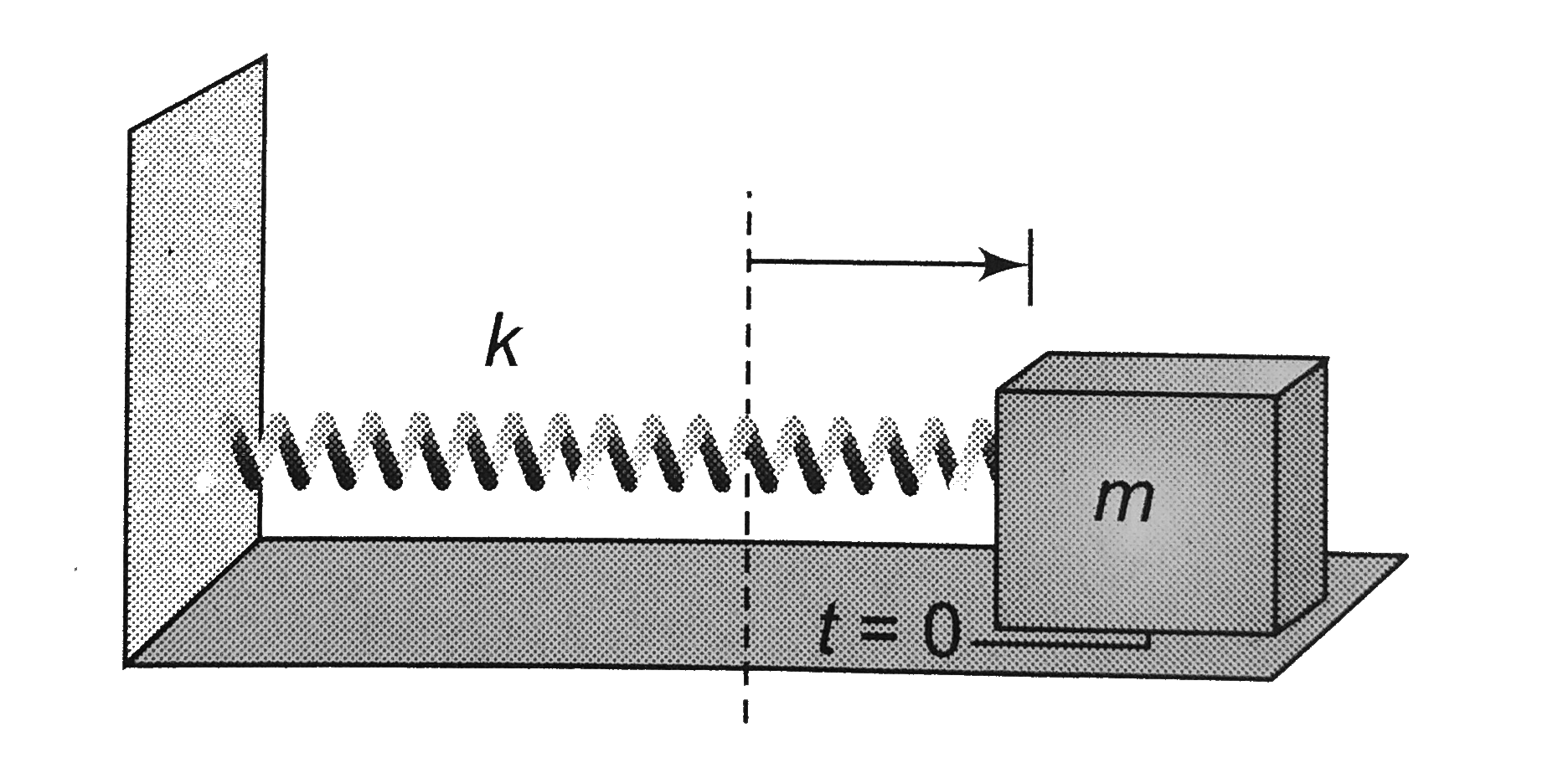
In a horizontal spring - mass m is released after being displaced toward right by same distance t=0 an a frictionless surface The phase angle of motion in ratio when it is first time passing through equlibrium possition is equal to
π2
π
3π2
0
The correct Answer is:B
Phase of the motion is (ωt+ϕ)
Using x=Asin(ωt+ϕ) and V=Aωcos(ω+ϕ)
for condition at t=0→x=A and V=0 then ϕ=π2 when it passes equilibrium for the first time
t=T4
Phase 2πT.T4+π2=π
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm25videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum19videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Velocity , Acceleration And Energy Of Simple Harmonic Motion40videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
A block of mass M is lying on a frictionless horizontal surface and it connected to a spring of spring constant k, whose other end is fixed to a wall, system executes simple harmonic motion of amplitude A0, when the block is passing through its equilibrium positions, an object of mass m is put on it and the two move together with a new time period T and amplitude A. Find the value of T and A in terms of given constants.
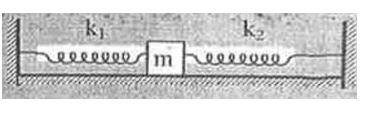
View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :
 AA√M−mMBA√MM+mCA√M+mMDA√MM−m
AA√M−mMBA√MM+mCA√M+mMDA√MM−m - Question 2 - Select One
A mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
 A√(M+m)MAB√(M−m)MAC√M(M+m)AD√M(M−m)A
A√(M+m)MAB√(M−m)MAC√M(M+m)AD√M(M−m)A - Question 3 - Select One

A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 View Solution
View SolutionA block of mass m attached to a massless spring is performing oscillatory motion of amplitude A on a frictionless horizontal plane. If half of the mass of the block off when it is passing through its mean position, the amplitude of oscillation for the remaining system become fA. The value of f is .
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 View Solution
View SolutionA light spring of force constant k is attached to a block of mass M placed on a horizontal firctionless surface from its one end and other end is fixed to a right support. The system is executing S.H.M. of amplitude A1 and time period T1. At some instant, the block passed through the equilibrium position and a small object of mass m is placed on it. The new amplitude and time period of the system now becomes A2 and T2 respectively.
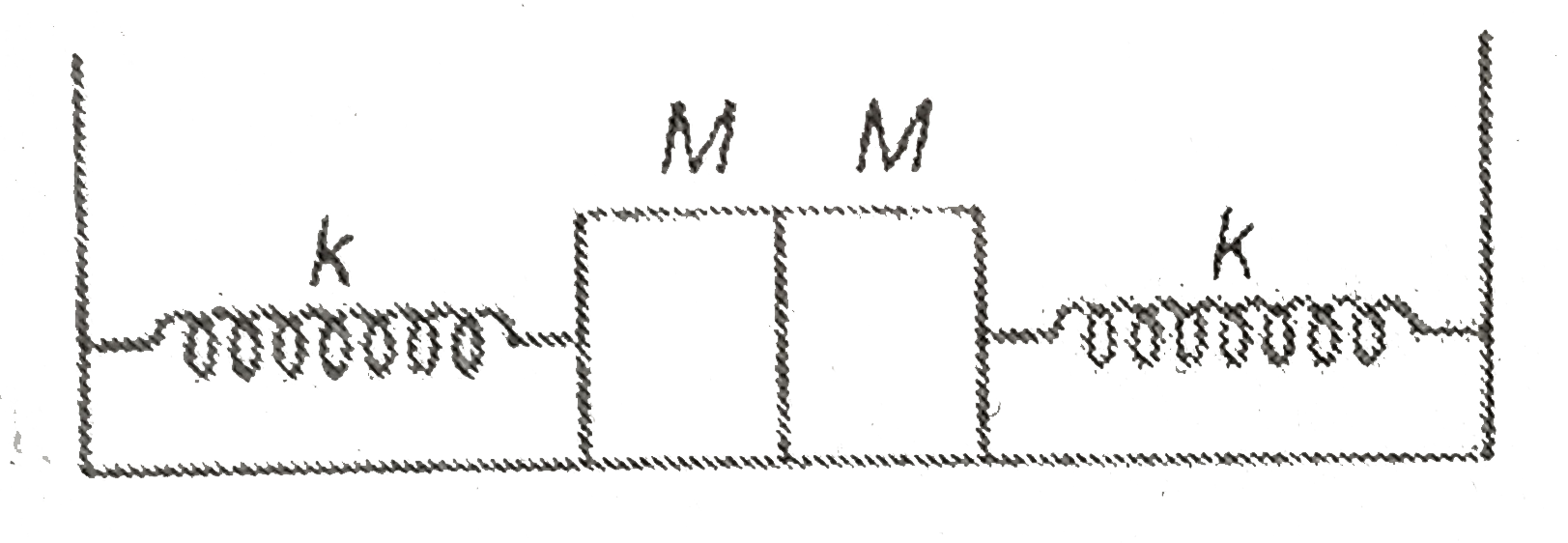
The ratio T2T1 isView SolutionAn assembly of identicl spring mass system is placed on a smooth horizontal surface as shown. Initially the springs are relaxed. The left mass is displaced to the left while the right mass is displaced to the right and released. The resulting collision is elastic. The time period of the oscillatins of the system is.
 View Solution
View Solution

