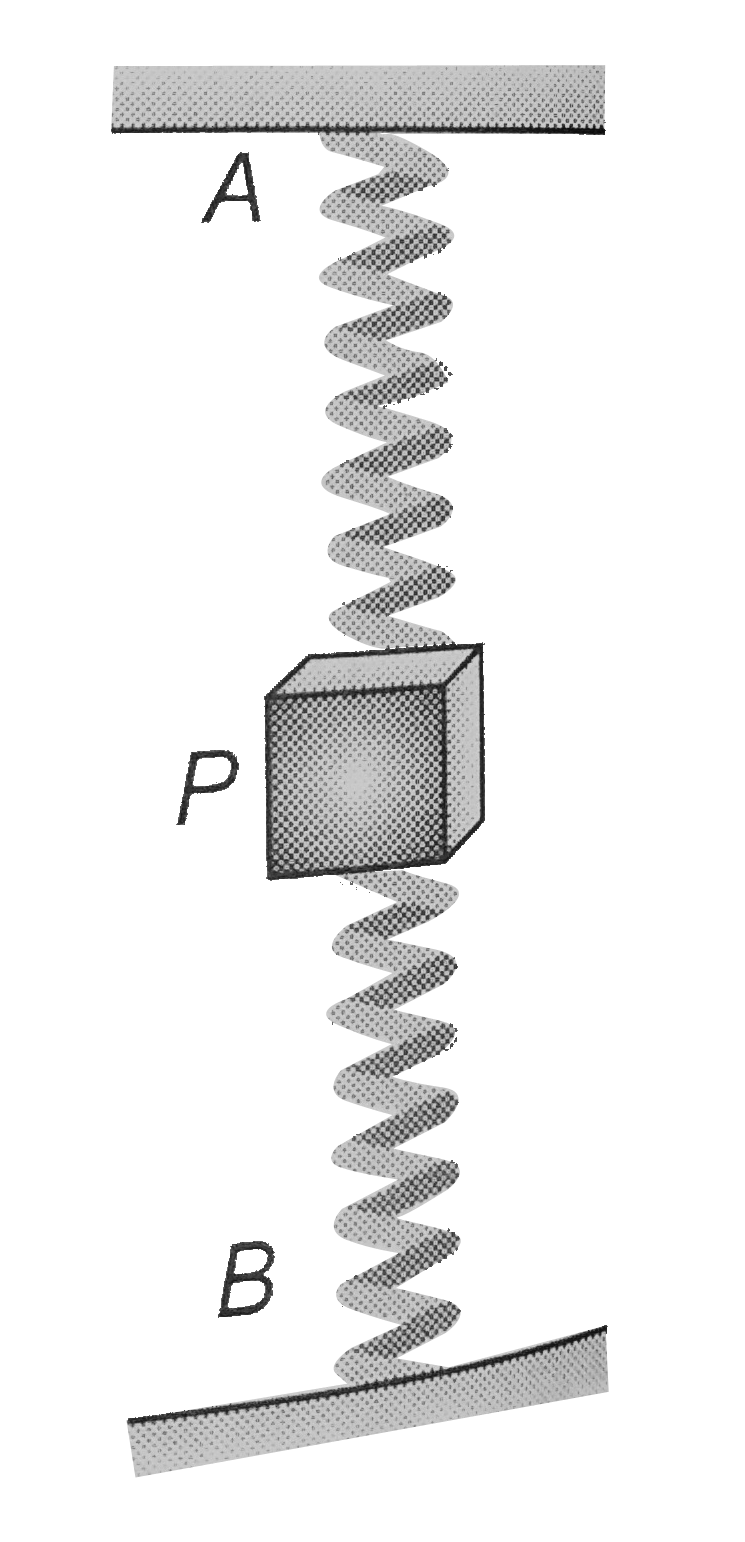
Two identical spring are attached to a small block P The other ends of the springs are fixed at A and B. when P is equilibrium the extension of top spring is 20cm and extension of bottom spring is 10cm The period at small vertical oscillation of p about its equilibrium position is (use g=9.8m/s2)
2π7sec
π7sec
2π5sec
none of these
The correct Answer is:B
Mg=K×20−K×10⇒K=mg10/100N/m
T=2π√MK
T=2π√149×4=π7sec
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm
25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum
19 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Velocity , Acceleration And Energy Of Simple Harmonic Motion
40 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
Consider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
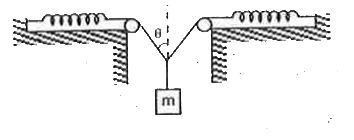
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
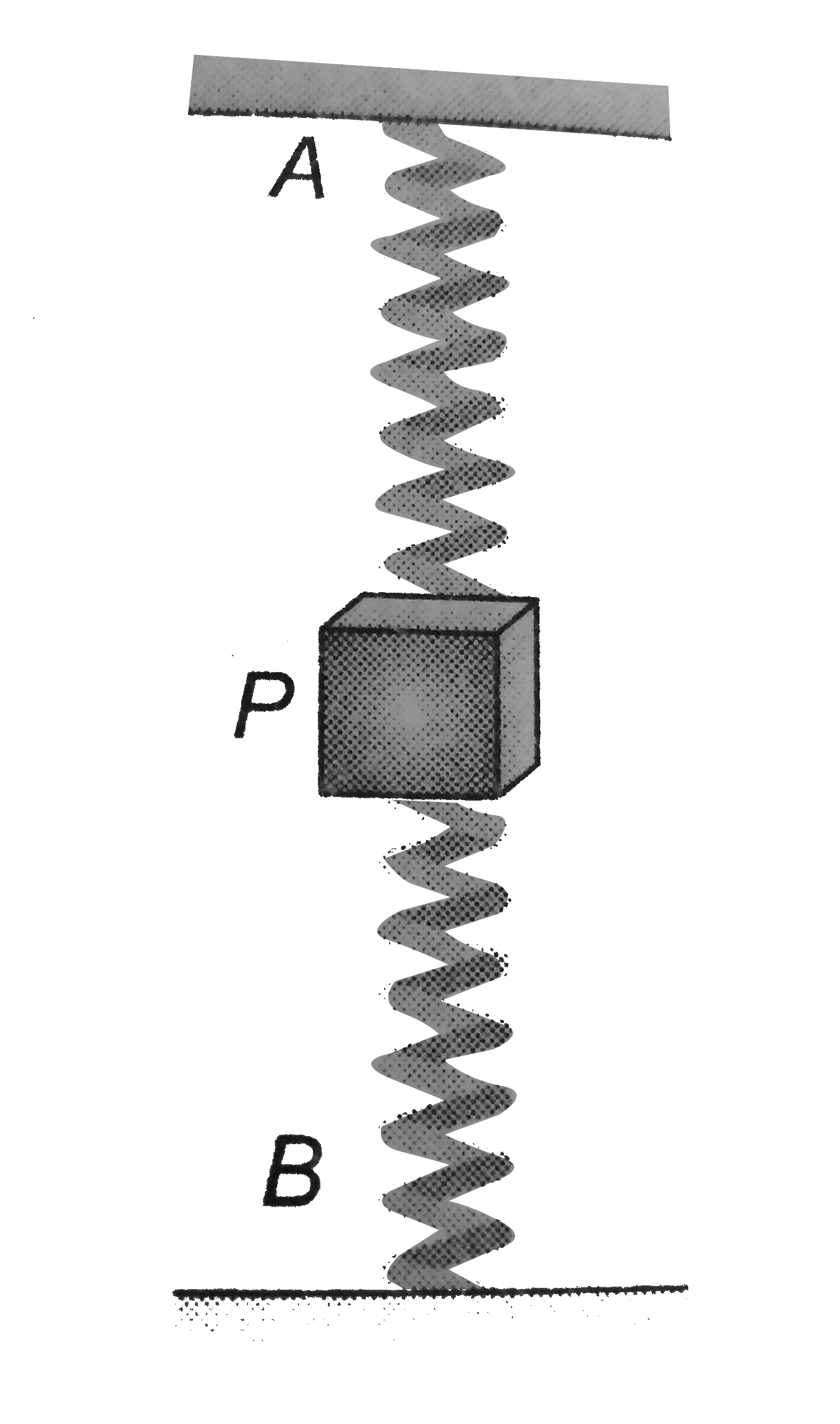
Two identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)
 A2π7secBπ7secC2π5secDnone of these
A2π7secBπ7secC2π5secDnone of theseIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
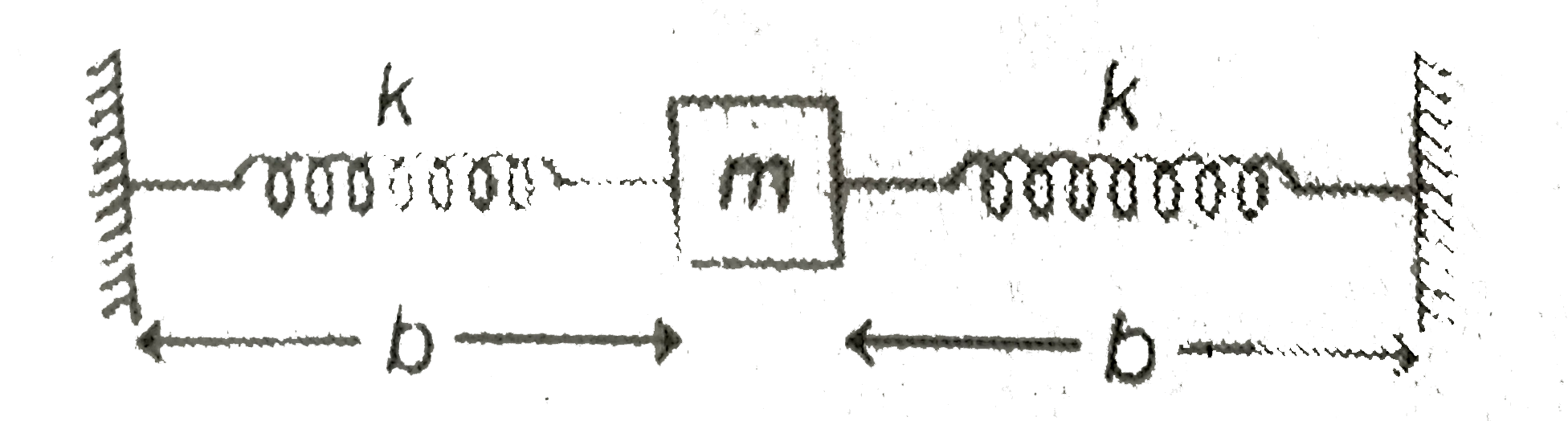 A2π√mbk(b−1)B2π√mb2k(b−l)C2π√(mb−lkb)D2π√(mb−l2kb)
A2π√mbk(b−1)B2π√mb2k(b−l)C2π√(mb−lkb)D2π√(mb−l2kb)The vertical extension in a light spring by a weight of 1 kg suspended from the wire is 9.8 cm . The period of oscillation
A20π cmB2πsecC2π/10secD200πsec
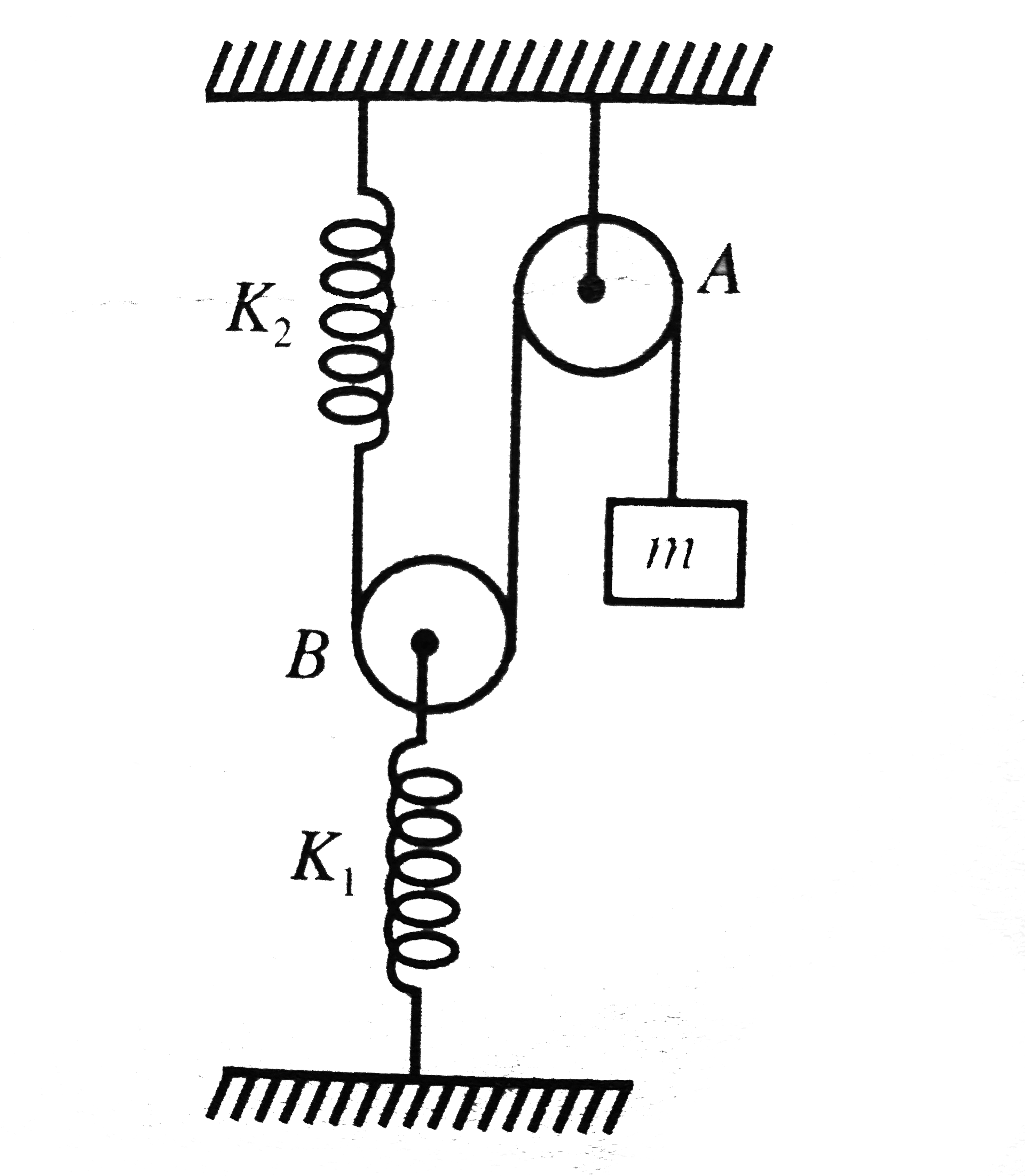
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
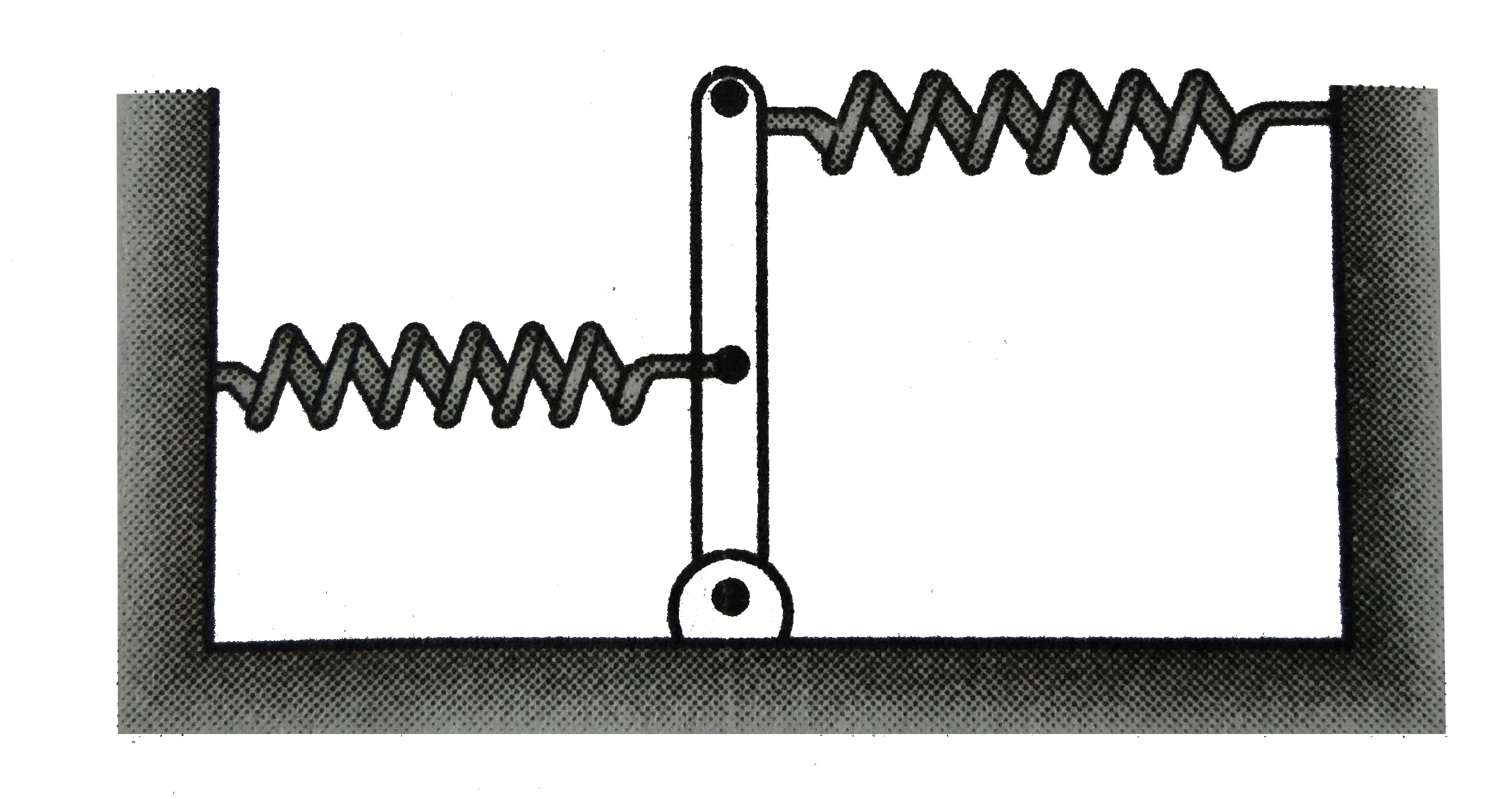
View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionTwo identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

View SolutionConsider a block symmetrically attached to two.identical massless springs by means of strings passing over light frictionless pulleys as shown in.the figure. In the equilibrium position extension in each spring is 0.5m. The time period of small vertical oscillation of the block is T second. Find the value of 5√3πT.
'(##CEN_KSR_PHY_JEE_C16_E01_027_Q11##)'
View Solution
