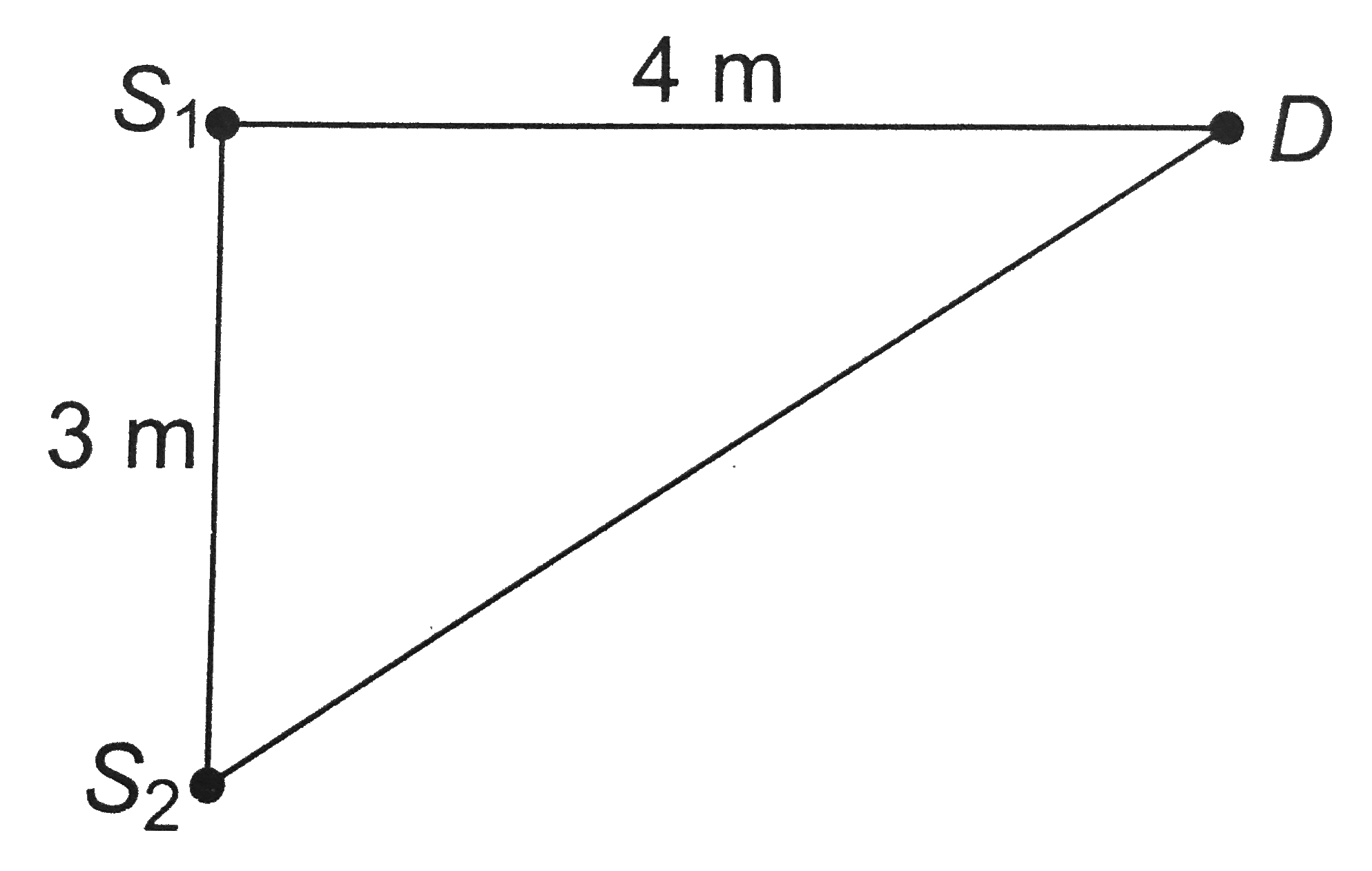
In the figure the intensity of waves arriving at D from two coherent sources S1 and S2 is I0 The wavelength of the wave is λ=4m. Resultant intensity at D will be:
4I0
I0
2I0
zero
The correct Answer is:C
Path differences, Δx=S2D−S1D=5−4=1m
The corresponding phase difference will be
ϕ=2πλΔx=2π4,1=π2
Using I=I1+I2+√I1I2cosϕ.
I=I0+I0+2√I0I0cos(π)2=2I0
Topper's Solved these Questions
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Beats
20 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Stationary Waves
20 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Equation And Energy Of Progressive Wave
16 Videos
- VECTORSBOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test
29 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
Similar Questions
The intensities of two light sources are I and 91 .If the phase difference between the waves is pi then resultant intensity will be :-
View SolutionTwo waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
View Solution
Knowledge Check
In the figure , the intensity of waves arriving at D from two coherent soucrces s1ands2isI0. The wavelength of the wave is λ=4m . Resultant intensity at D will be
 A4l0Bl0C2l0Dzero
A4l0Bl0C2l0Dzero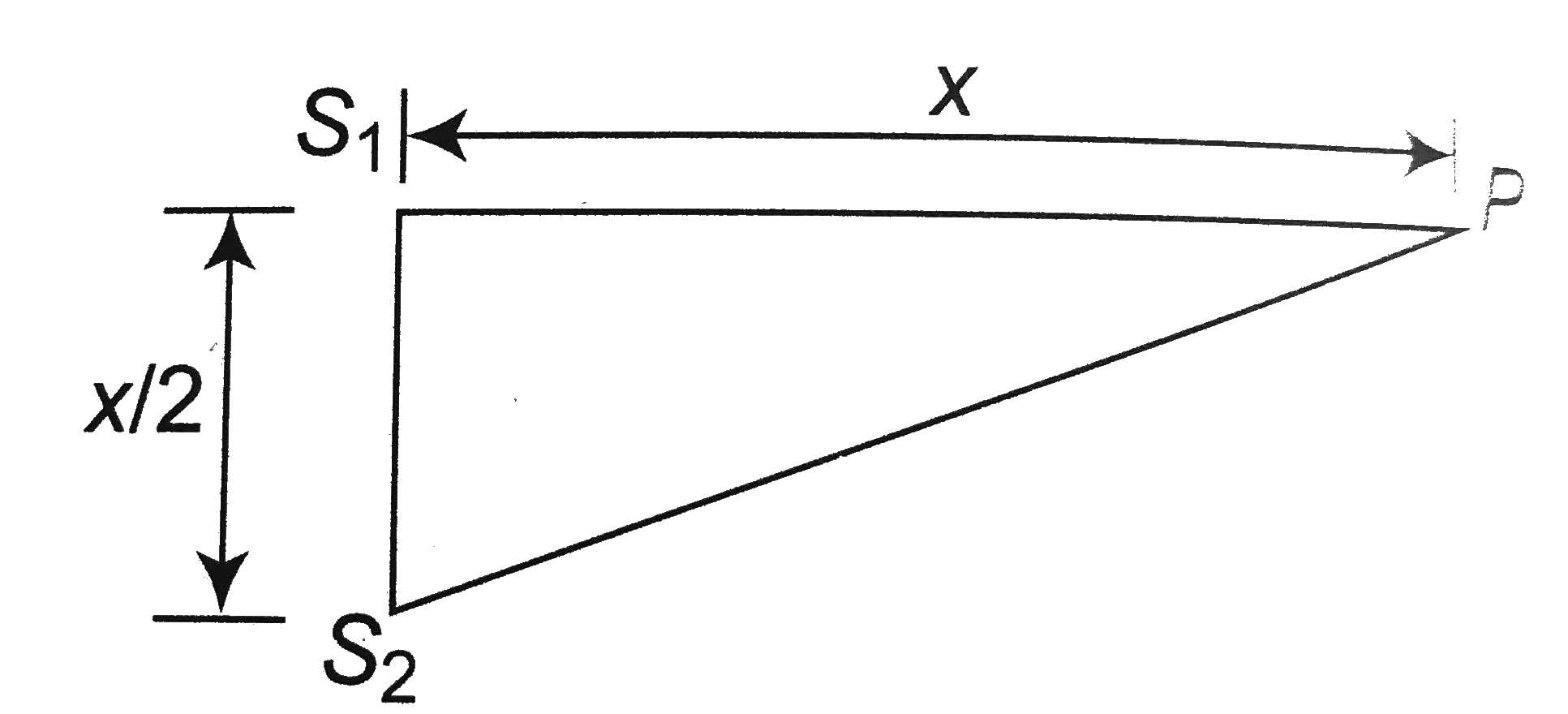
The wavelength of the waves arriving at P from two coherent sources S1 and S2 is 4m, while intensity of each wave is I0. The resultant intensity at P is 2I0. Find the minimum value of S2PAx√52B2xC(x+1)D(x+√2)If the intensity of the waves obvserved by two coherent sources is 1. Then the intensity of resultant waves in constructive interferences will be:
A21B41C1DNone of the above
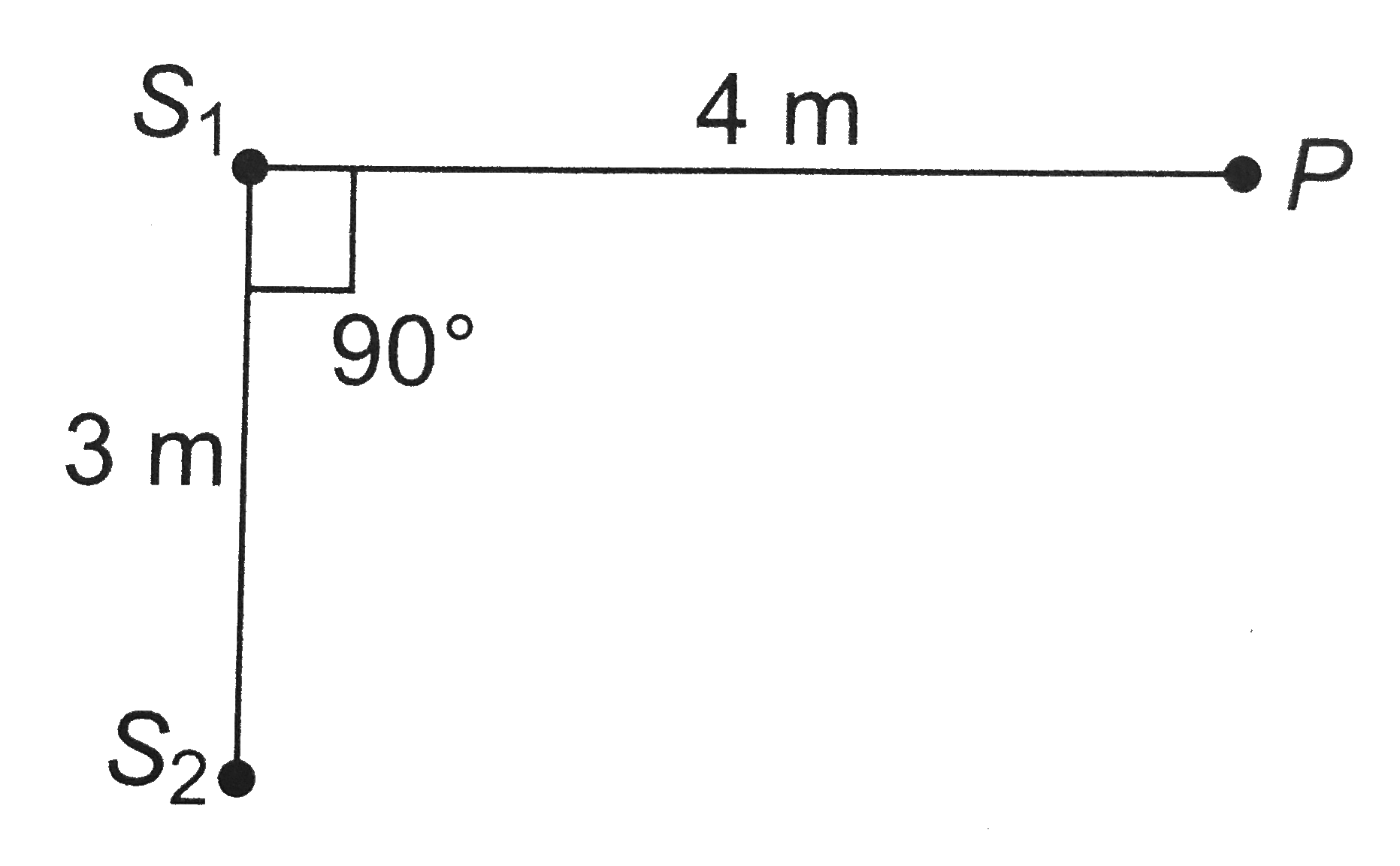
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View SolutionLight waves from two coherent sources having intensities I and 2I cross each other at a point with a phase difference of 60∘. The intensity at the point will be
View SolutionThe maximum intensities produced by two coherent waves of intensity I1 and I2 will be:
View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
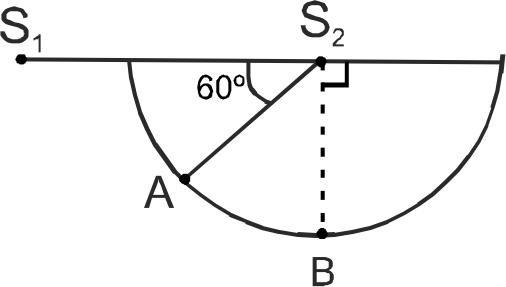
The intensity o sound of B due to S1andS2 is :
View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
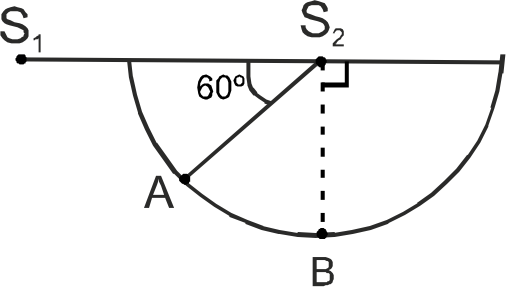
The intensity of sound at B due to S1 only is :
View Solution