Two waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
Zero
2a2
5a2
6a2
The correct Answer is:A
To solve the problem, we need to analyze the interference of two coherent waves at point R, given that the path difference S2R−S1R=1.5λ.
1. Identify the Given Information:
- Amplitudes of the waves from sources S1 and S2 are equal, denoted as A.
- The path difference is given as S2R−S1R=1.5λ.
2. Understanding Path Difference:
- The path difference of 1.5λ can be expressed as 32λ.
- This indicates that the waves are out of phase by 1.5λ.
3. Determine the Type of Interference:
- A path difference of 32λ corresponds to an odd multiple of λ2 (specifically 32λ).
- This results in destructive interference because the waves are out of phase by 180∘ (or π radians).
4. Calculate the Resultant Amplitude:
- For destructive interference, the resultant amplitude AR can be calculated using the formula:
AR=|A1−A2|
- Since both amplitudes are equal (A1=A2=A):
AR=|A−A|=|0|=0
5. Calculate the Intensity:
- The intensity I of a wave is proportional to the square of the amplitude:
I∝A2
- Since the resultant amplitude AR=0:
IR=A2R=02=0
6. Conclusion:
- The intensity at point R is 0.
Final Answer:
The intensity at point R would be 0.
- Amplitudes of the waves from sources S1 and S2 are equal, denoted as A.
- The path difference is given as S2R−S1R=1.5λ.
- The path difference of 1.5λ can be expressed as 32λ.
- This indicates that the waves are out of phase by 1.5λ.
- A path difference of 32λ corresponds to an odd multiple of λ2 (specifically 32λ).
- This results in destructive interference because the waves are out of phase by 180∘ (or π radians).
- For destructive interference, the resultant amplitude AR can be calculated using the formula:
AR=|A1−A2|
- Since both amplitudes are equal (A1=A2=A):
AR=|A−A|=|0|=0
- The intensity I of a wave is proportional to the square of the amplitude:
I∝A2
- Since the resultant amplitude AR=0:
IR=A2R=02=0
- The intensity at point R is 0.
The intensity at point R would be 0.
Topper's Solved these Questions
Similar Questions
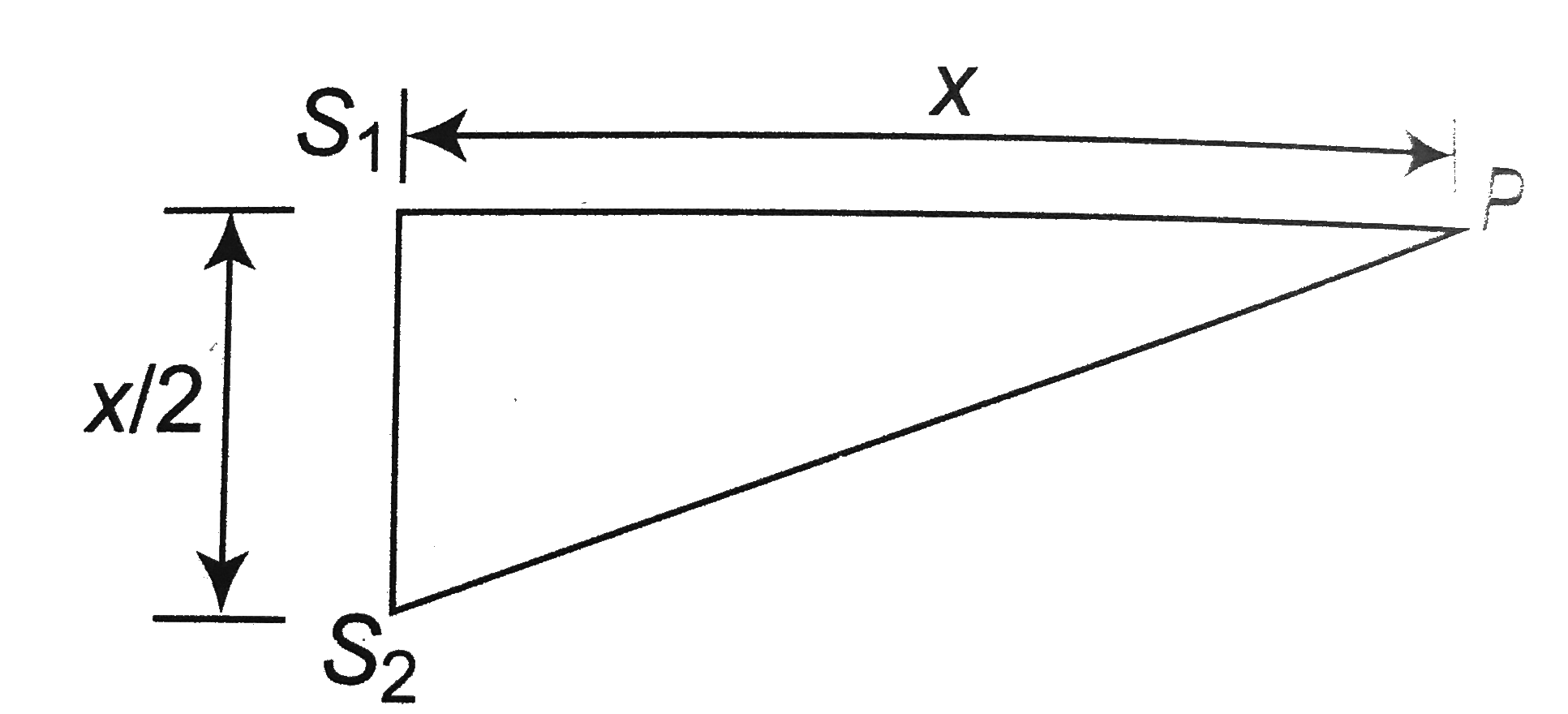
The wavelength of the waves arriving at P from two coherent sources S1 and S2 is 4m, while intensity of each wave is I0. The resultant intensity at P is 2I0. Find the minimum value of S2P
View SolutionIn the figure , the intensity of waves arriving at D from two coherent soucrces s1ands2isI0. The wavelength of the wave is λ=4m . Resultant intensity at D will be

View Solution
Knowledge Check
Two sound waves each of wavelength λ and having the same amplitude A form two sources S1andS2 interfere at a point P. If the path difference S2P−S1P=λ3, then the amplitude of the resultant were at P will be
AAB2ACA/2D3A/2When two waves of intensities l1andl2 coming from coherent sources interfere at a point P, where phase difference is ϕ, then resultant intensity (lres) at point P would be
Alres=l1−l2−2√l1l2Blres=l1+l2+2√l1l2cosϕClres=l1+l2−2√l1l2cos2ϕDlres=(l1)2+(l2)2−2(l1l2)cos2ϕ
In the figure the intensity of waves arriving at D from two coherent sources S1 and S2 is I0 The wavelength of the wave is λ=4m. Resultant intensity at D will be:A4I0BI0C2I0Dzero
Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionIn the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
View SolutionIn terms of the ratio r of the amplitudes of two coherent waves producing an interference pattern, the ratio of the intensity maximum to intensity minimum in the pattern is
View SolutionS1andS2 are two coherent sources of radiations separated by distance 100.25λ, where λ is the wave length of radiation. S1 leads S2 in phase by π/2.A and B are two points on the line joining S1andS2 as shown in figure.The ratio of amplitudes of component waves from source S1andS2 at A and B are in ratio 1:2. The ratio of intensity at A to that of B (IAIB) is

View Solution
