Check the correctness of the relation h=2σcosθr2dg, where h is height , sigam is surface tension, θ is angle of contact, r is radius, d is density and g in acceleration due to gravity.
The correct Answer is:wrong
To check the correctness of the relation h=2σcosθr2dg, we will analyze the dimensions of both sides of the equation. If the dimensions match, the relation is dimensionally correct; if they do not, the relation is incorrect.
1. Identify the dimensions of each variable:
- Height (h): The dimension of height is length, denoted as (h)=L1.
- Surface Tension (σ): Surface tension is defined as force per unit length. The dimension of force is (F)=M1L1T−2. Therefore, the dimension of surface tension is:
(σ)=(F)(L)=M1L1T−2L1=M1L0T−2
- Angle of Contact (θ): The angle is dimensionless, so:
(θ)=M0L0T0
- Radius (r): The radius is also a length, so:
(r)=L1
- Density (d): Density is mass per unit volume. The dimension of volume is L3, so:
(d)=M1L3=M1L−3
- Acceleration due to Gravity (g): The dimension of acceleration is:
(g)=L1T−2
2. Calculate the dimensions of the right-hand side (RHS):
The RHS of the equation is:
2σcosθr2dg
Since 2 is a constant, it does not affect dimensions. The dimensions can be calculated as follows:
- Cosine of angle: (cosθ)=M0L0T0
- Dimensions of r2:
(r2)=(L1)2=L2
- Dimensions of d:
(d)=M1L−3
- Dimensions of g:
(g)=L1T−2
Now substituting these into the RHS:
(RHS)=(M1L0T−2)⋅(M0L0T0)(L2)⋅(M1L−3)⋅(L1T−2)
Simplifying this:
=M1L0T−2L2⋅M1L−3⋅L1T−2=M1L0T−2M1L2−3+1T−2=M1L0T−2M1L0T−2=M0L0T0
Thus, the dimensions of the RHS are dimensionless:
(RHS)=M0L0T0
3. Compare with the left-hand side (LHS):
The LHS is simply h, which has the dimension:
(LHS)=(h)=M0L1T0
4. Conclusion:
Since the dimensions of the LHS (M0L1T0) and the RHS (M0L0T0) do not match, we conclude that the relation is not dimensionally correct.
Final Answer:
The relation h=2σcosθr2dg is dimensionally incorrect.
- Height (h): The dimension of height is length, denoted as (h)=L1.
- Surface Tension (σ): Surface tension is defined as force per unit length. The dimension of force is (F)=M1L1T−2. Therefore, the dimension of surface tension is:
(σ)=(F)(L)=M1L1T−2L1=M1L0T−2
- Angle of Contact (θ): The angle is dimensionless, so:
(θ)=M0L0T0
- Radius (r): The radius is also a length, so:
(r)=L1
- Density (d): Density is mass per unit volume. The dimension of volume is L3, so:
(d)=M1L3=M1L−3
- Acceleration due to Gravity (g): The dimension of acceleration is:
(g)=L1T−2
The RHS of the equation is:
2σcosθr2dg
Since 2 is a constant, it does not affect dimensions. The dimensions can be calculated as follows:
- Cosine of angle: (cosθ)=M0L0T0
- Dimensions of r2:
(r2)=(L1)2=L2
- Dimensions of d:
(d)=M1L−3
- Dimensions of g:
(g)=L1T−2
(RHS)=(M1L0T−2)⋅(M0L0T0)(L2)⋅(M1L−3)⋅(L1T−2)
Simplifying this:
=M1L0T−2L2⋅M1L−3⋅L1T−2=M1L0T−2M1L2−3+1T−2=M1L0T−2M1L0T−2=M0L0T0
Thus, the dimensions of the RHS are dimensionless:
(RHS)=M0L0T0
The LHS is simply h, which has the dimension:
(LHS)=(h)=M0L1T0
Since the dimensions of the LHS (M0L1T0) and the RHS (M0L0T0) do not match, we conclude that the relation is not dimensionally correct.
The relation h=2σcosθr2dg is dimensionally incorrect.
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Test Your Grip
50 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Fill in the blanks
50 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Value Based Questions
5 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - multiple choice Questions
13 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
Similar Questions
Test if the following equation is dimensionally correct: h=(sScosθrpg) where h= height, S= surface tension, p= density, r=radius, and g= acceleration due to gravity.
View SolutionIf g is acceleration due to gravity on the surface of the earth,having radius R ,the height at which the acceleration due to gravity reduces to g/2 is
View Solution
Knowledge Check
Given as : h=2Scosθrρg where S is the surface tension of liquid, r is the radius of capillary tube. ρ is the density and g is acceleration due to gravity then dimensional formula for S is:
A[ML0T−2]B[M0LT−2]C[ML2T−2]D[M0L0T−3]The binding energy of an object of mass m placed on the surface of the earth r is (R = radius of earth, g = acceleration due to gravity)
AmgR/2Bmg RCmgR4DmgR8Surface tension arises from the cohesive force between the surface molecules. Interplay between cohesion and adhesion force make the surface inclined at acute or obtuse angle with the contacting solid surfaces. This causes a capillary rise (or fail) given as h=2Tcosθρgr, where θ= angle of contact T= surface tension ρ= density of the liquid, g= acceleration due to gravity and r= radius of the capillary tube.
Q. In capillary action θ can be:A0∘B90∘C90∘<θ<180∘Dall of these
The pressure at a depth h in a liquid of density d is given by pressure = __ , where g is the acceleration due to gravity.
View SolutionSurface tension arises from the cohesive force between the surface molecules. Interplay between cohesion and adhesion force make the surface inclined at acute or obtuse angle with the contacting solid surfaces. This causes a capillary rise (or fail) given as h=2Tcosθρgr, where θ= angle of contact T= surface tension ρ= density of the liquid, g= acceleration due to gravity and r= radius of the capillary tube.
Q. If the vessel accelerates up, capillary rise,
View SolutionSurface tension arises from the cohesive force between the surface molecules. Interplay between cohesion and adhesion force make the surface inclined at acute or obtuse angle with the contacting solid surfaces. This causes a capillary rise (or fail) given as h=2Tcosθρgr, where θ= angle of contact T= surface tension ρ= density of the liquid, g= acceleration due to gravity and r= radius of the capillary tube.
In capillary rise:
View SolutionWhat will be the acceleration due to gravity at height h if h gt gt R . Where R is radius of earth and g is acceleration due to gravity on the surface of earth
View Solution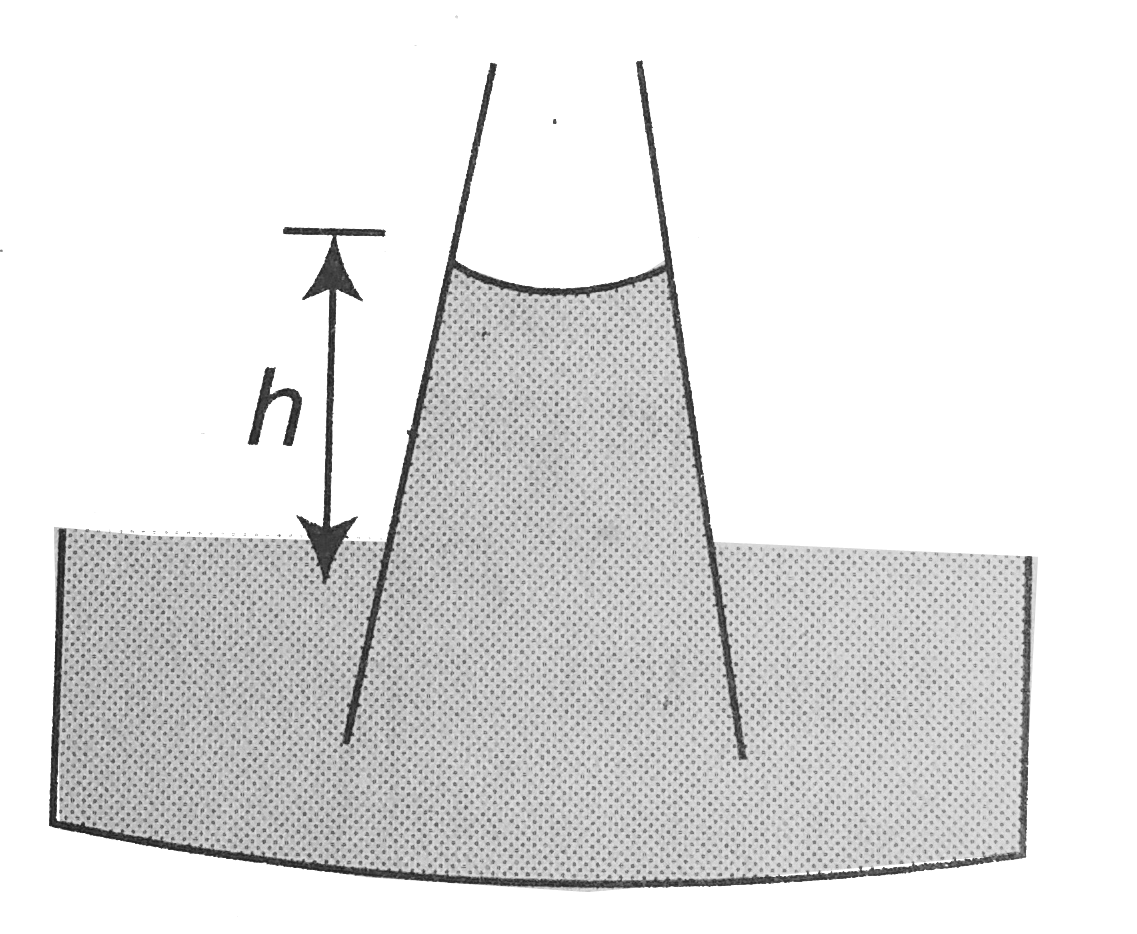
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View Solution
