The cirtical velocity (υ) of flow of a liquied through a pipe of radius (r ) is given by υ=ηρr where ρ is density of liquid and η is coefficient of visocity of the liquied. Check if the relaiton is correct dimensinally.
The correct Answer is:Correct
Step by step video, text & image solution for The cirtical velocity (upsilon) of flow of a liquied through a pipe of radius (r ) is given by upsilon = (eta)/(rho r) where rho is density of liquid and eta is coefficient of visocity of the liquied. Check if the relaiton is correct dimensinally. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Test Your Grip
50 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Fill in the blanks
50 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Value Based Questions
5 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - multiple choice Questions
13 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
Similar Questions
The critical velocity of the flow of a liquid through a pipe of radius 3 is given by vc=(Kηrp), where p is the density and η, is the coefficient of viscosity of liquid. Check if this relation is dimentionally correct.
View SolutionThe rate flow (V) of a liquid through a pipe of radius (r ) under a pressure gradient (P//I) is given by V=π8PR4Iη, Where η is coefficient of visocity of the liquied. Check whether the formula is correct or not.
View Solution
Knowledge Check
A small metal sphere of radius a is falling with a velocity υ through a vertical column of a viscous liquid. If the coefficient of viscosity of the liquid is η, then the sphere encounters an opposing force of
A6πηa2υB6ηυπaC6πηaυDπηυ6a3In dimension of circal velocity v0 liquid following through a take are expressed as (ηxρyrz) where η,ρandrare the coefficient of viscosity of liquid density of liquid and radius of the tube respectively then the value of x,y and z are given by
A1,1,1B1,−1,−1C−1,−1,1D−1,−1,−1The rate of flow Q (volume of liquid flowing per unit time) through a pipe depends on radius r, length L of pipe, pressure difference p across the ends of pipe and coefficient of viscosity of liquid η as Q∝rapbηcLd, then
Aa=4,b=1,c=−1,d=−1Ba=4,b=−1,c=1,d=−1Ca=4,b=1,c=1,d=−1Dvalues of a,b,c ang d cannot be detemind
Using the method of dimensions, derive an expression for rate of flow (v) of a liquied through a pipe of radius (r ) under a pressure gradient (P/I) Given that V also depends on coefficient of viscosity (η) of the liquied.
View SolutionThe volume of a liquied flowing out per second of a pipe of length I and radius r is written by a student as υ=π8Pr4ηI where P is the pressure difference between the two ends of the pipe and η is coefficient of viscosity of the liquid having dimensioal formula ML−1T−1. Check whether the equation is dimensionally correct.
View SolutionCheck the accuracy of the relation η=π8Pr4lV
Here, P is pressure, V= rate of flow of liquid through a pipe, η is coefficient of viscosity of liquid.
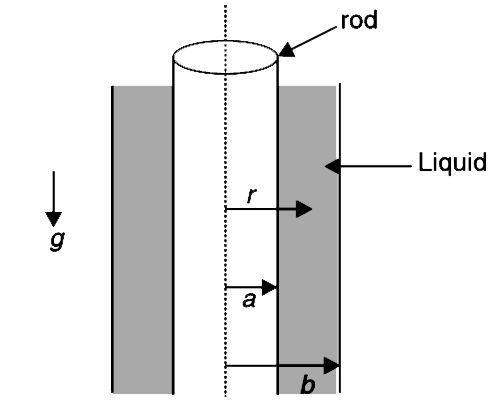
View SolutionA vertical steel rod has radius a. The rod has a coat of a liquid film on it. The liquid slides under gravity. It was found that the speed of liquid layer at radius r is given by
v=ρgb22ηln(ra)−ρg4η(r2−a2)
Where b is the outer radius of liquid film, η is coefficient of viscosity and ρ is density of the liquid.
(i) Calculate the force on unit length of the rod due to the viscous liquid?
(ii) Set up the integral to calculate the volume flow rate of the liquid down the rod. [you may not evaluate the integral]
View SolutionDerive by the method of dimensions, an expression for the volume of a liquid flowing out per second through a narrow pipe. Asssume that the rate of flow of liwquid depends on
(i) the coeffeicient of viscosity η of the liquid
(ii) the radius 'r' of the pipe and
(iii) the pressure gradient Pl along the pipte. Take K=π8.
View Solution
