A food packet is released from a helicopter which is trising steadily at 3ms−1. After 3seconds, (i) what is the velocity of the packet? (ii) how far is it below the helicopter ? Take g=9.8m/s2.
To solve the problem step by step, we will break it down into two parts as per the question.
Given Data:
- Velocity of helicopter (upward) = 3m/s
- Time after release = 3s
- Acceleration due to gravity, g=9.8m/s2
Part (i): Finding the velocity of the packet after 3 seconds
1. Identify the initial velocity (U):
- The packet is released from a helicopter that is rising at 3m/s. Since we take downward as positive, the initial velocity of the packet will be:
U=−3m/s
2. Use the equation of motion to find the final velocity (V):
- The equation of motion is given by:
V=U+at
- Here, a=g=9.8m/s2 (downward), and t=3s.
- Substitute the values into the equation:
V=−3+(9.8×3)
- Calculate:
V=−3+29.4=26.4m/s
Part (ii): Finding how far the packet is below the helicopter after 3 seconds
1. Calculate the displacement of the packet (S):
- Use the equation of motion:
S=Ut+12at2
- Substitute the values:
S=(−3)(3)+12(9.8)(32)
- Calculate:
S=−9+12(9.8)(9)=−9+44.1=35.1m
2. Calculate the distance the helicopter has traveled upward:
- The helicopter moves upward at a constant speed of 3m/s for 3s:
Distancehelicopter=3×3=9m
3. Total distance below the helicopter:
- The total distance below the helicopter is the sum of the distance the packet has fallen and the distance the helicopter has risen:
Total distance=S+Distancehelicopter=35.1+9=44.1m
Final Answers:
(i) The velocity of the packet after 3 seconds is 26.4m/s (downward).
(ii) The packet is 44.1m below the helicopter.
- Velocity of helicopter (upward) = 3m/s
- Time after release = 3s
- Acceleration due to gravity, g=9.8m/s2
- The packet is released from a helicopter that is rising at 3m/s. Since we take downward as positive, the initial velocity of the packet will be:
U=−3m/s
- The equation of motion is given by:
V=U+at
- Here, a=g=9.8m/s2 (downward), and t=3s.
- Substitute the values into the equation:
V=−3+(9.8×3)
- Calculate:
V=−3+29.4=26.4m/s
- Use the equation of motion:
S=Ut+12at2
- Substitute the values:
S=(−3)(3)+12(9.8)(32)
- Calculate:
S=−9+12(9.8)(9)=−9+44.1=35.1m
- The helicopter moves upward at a constant speed of 3m/s for 3s:
Distancehelicopter=3×3=9m
- The total distance below the helicopter is the sum of the distance the packet has fallen and the distance the helicopter has risen:
Total distance=S+Distancehelicopter=35.1+9=44.1m
(i) The velocity of the packet after 3 seconds is 26.4m/s (downward).
(ii) The packet is 44.1m below the helicopter.
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Problems for practice
67 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Problems for practice
45 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Problems for practice
25 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
A food packet is released from a helicopter which is rising steadily at 2ms−1 , After two second (i) What is the velocity of the packet ? (ii)How far is it below the helicopter?
Take g=9.8ms−2 .
View SolutionA packet is dropped from a helicopter, which is ascending at a rate of 16m/s , when it is at a height of 14.4m above the ground.
(i) How much time it will take the packet to reach the ground?
(ii) With what velocity it will hit the ground?
View Solution
Knowledge Check
A ball is dropped from a balloon which is rising up with a speed of 2 m/s. After 2 s the velocity of the packet is
A20 m/sB18 m/sC22 m/sDnoneA packet is dropped from a helicopter rising up with velocity 2ms−1. The velocity of the packet after 2 seconds will be
A18 m/sB10 m/sC8 m/sD2 m/sA stone is released from an aeroplane which is rising with upward acceleration 5ms−2 . Here g=10ms−1 The seconds after the release , the saparation between stone and aeroplane will be
A10 mB20 mC30 mD25 m
A body is thrown horizontal from the top of a tower and strikes the ground after two seconds at angle of 45∘ with the horizontal. Find the height of the tower and the speed with which the body was thrown. Take g=9.8ms−2.
View SolutionA packet is dropped from a balloon which is going upwards with the velocity 12m/s. The velocity of the packet after 2 seconds will be
View SolutionA particle starts from the point (0m,8m) and moves with uniform velocity of 3ˆim/s. After 5 seconds, the angular velocity of the particle about the origin will be :
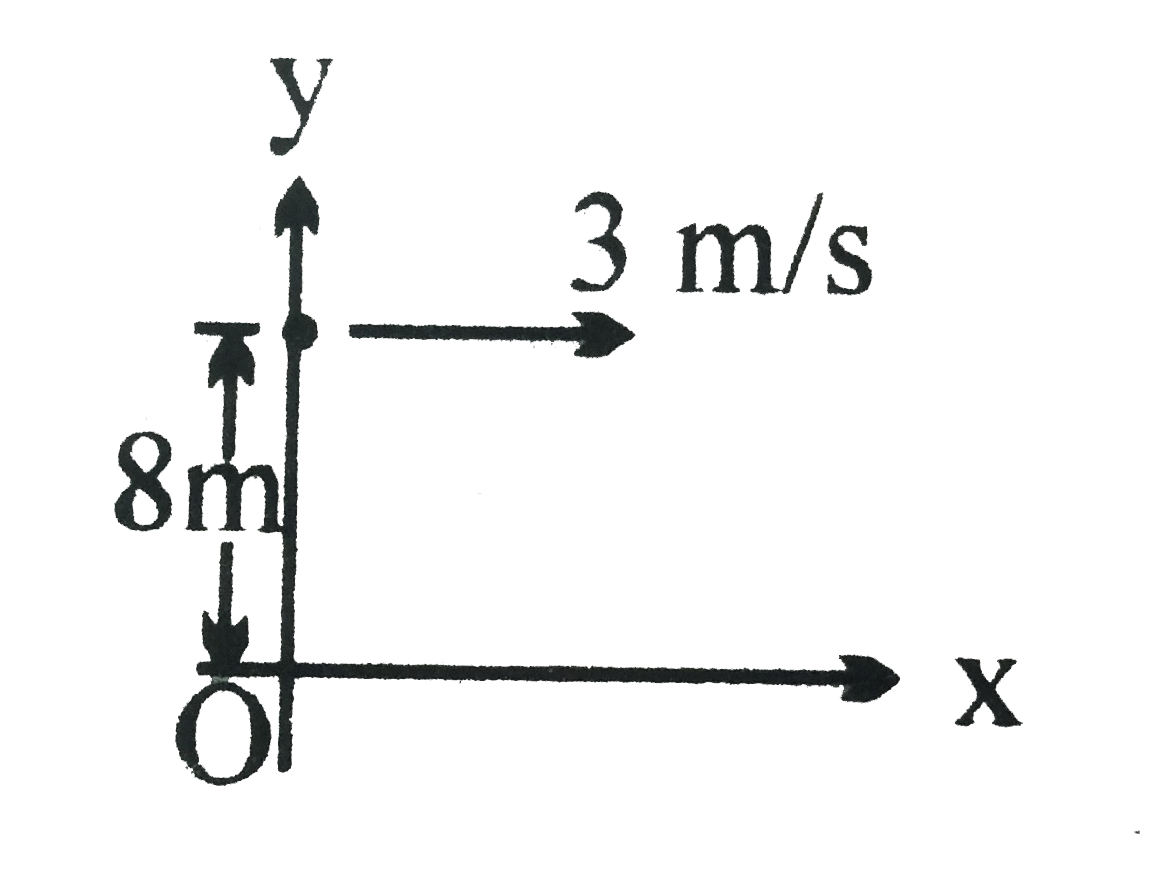 .
.
View SolutionA packet is released from a balloon which is moving upward when the balloon is at a height 200 m above ground. The packet reaches the ground in 8 sec. Speed of the balloon when the packet is released, is: (Take g=10m/s2)
View SolutionA packet is dropped from a flight ascending with a velocity at height of 10km. If the packet takes 100s to reach the ground, then the velocity of the flight is (take g=10ms−2)
View Solution
