Question

A vector $\overrightarrow{A}$ of magniude (A) is turned through an angle $\theta$. Calculate the change in the magnitude of vector.

Options

A. ` 2 a sin (alpha //2)`
B. ` 2 a cos (alpha//2 )`
C. ` 2 a tan (alpha //2)`
D. `2 a cot (alpha //2)`

Answer

A

Explanation

Refer to Fig. 2 (C F). 49, the change in position vector ` Delta vec a` is represented by ` vec (OQ)`.
.
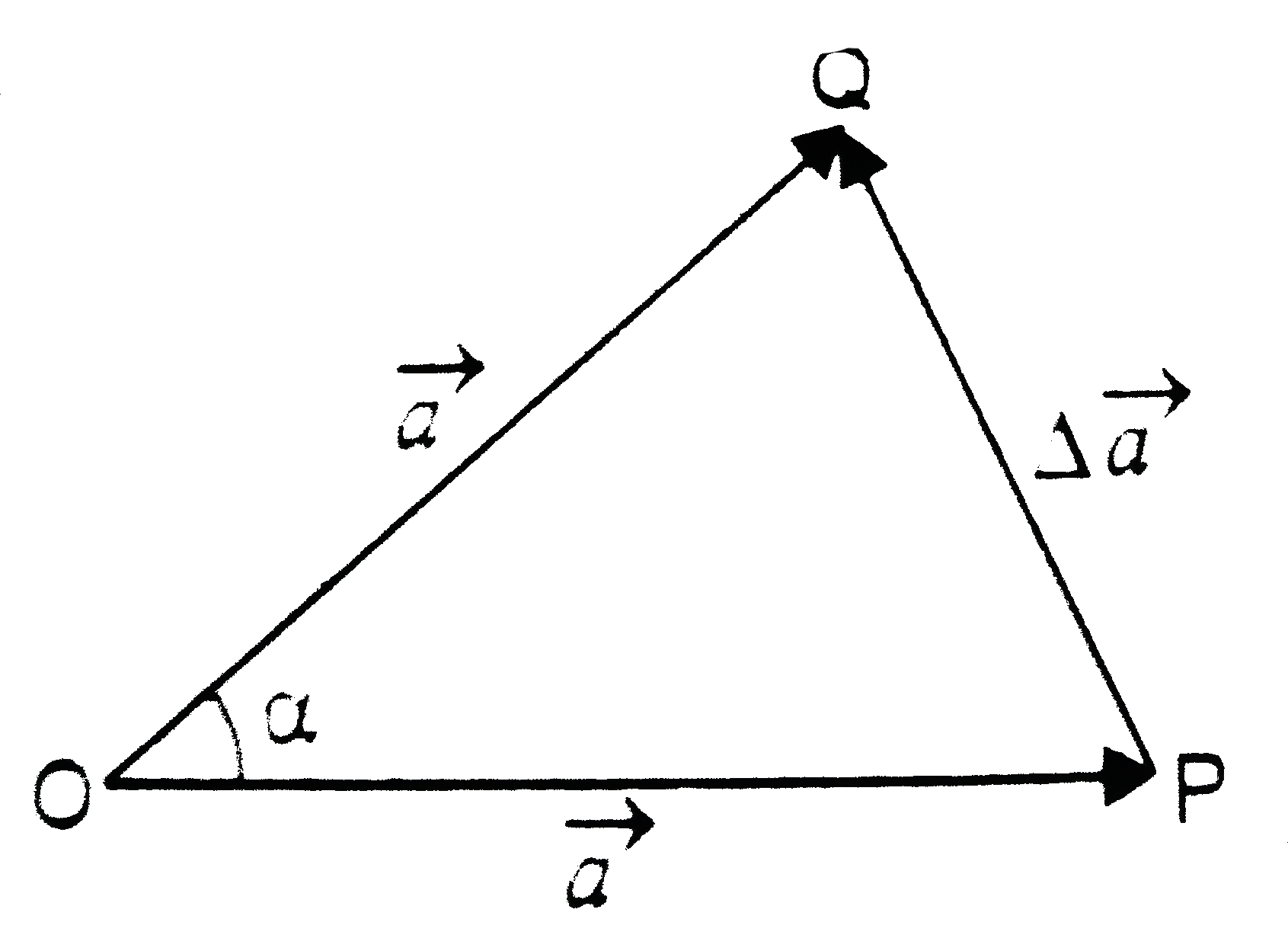From ` Delta` law of vectors,
` vec (PQ) = vec (OQ) - vec (OP) = vec (OQ) + (-vec OP)`
Angle between ` vec (OQ) and ` (- vec (OP)` is (1 80^2- alpha)`
:. (Delta a)^2 = a^2 +a^2 + 2 a^2 cos (18-0^2- alpha)`
` = 2 a^2 - 2 a^2 cos alpha a^2 (1 - cos alpha)`
` = 2 a^2 [ 1 -1 + 2 sin^2 alpha//2]`
` 4 a^2 sin^2 alpha //2`
` :. Delat a = 2 sin alpha //2`.